Visual Projection factor in VINS

1. 基于图优化的滑动窗口紧耦合视觉惯性里程计

对于一个基于非线性图优化且利用滑动窗口固定计算量的紧耦合视觉惯导里程计，求解 Bundle Adjustment 具有如下结构¹：

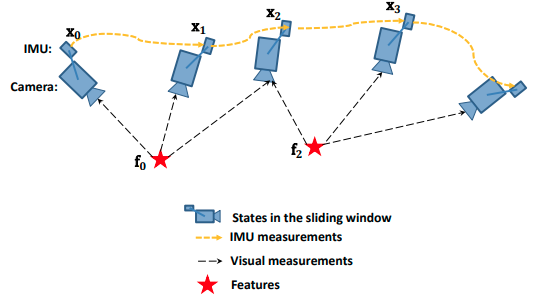
其中，非线性优化器中的优化向量有位置、速度、姿态、IMU 偏移量、特征、相机-IMU 外参：

$$ \begin{align*} \mathcal{X} &= [\mathbf{x} _0, \mathbf{x} _1, \cdots \mathbf{x} _n, \mathbf{x} _c^b, t _d, \lambda _0, \lambda _1, \cdots \lambda_m] \newline \mathbf{x} _k &= [\mathbf{p} _{b_k}^w, \mathbf{v} _{b_k}^w, \mathbf{q} _{b_k}^w, \mathbf{b} _a, \mathbf{b} _g], k \in [0, n] \newline \mathbf{x} _c^b &= [\mathbf{p} _c^b, \mathbf{q} _c^b] \newline t _d &= t _{imu} - t _{cam} \end{align*} \tag{1.1} $$

最小二乘求解如下：

$$ \min _\mathcal{X} \left\lbrace \underbrace{\lVert\mathbf{r} _b - \mathbf{H} _p \mathcal{X} \rVert^2} _{\text{Prior from marginalization}} + \overbrace{\underbrace{\sum _{k\in\mathcal{B}} \lVert \mathbf{r} _\mathcal{B}(\hat{\mathbf{z}} _{b _{k+1}}^{b _k}, \mathcal{X}) {\lVert}^{2} _{P _{b _{k+1}^{b_k}}}} _{\text{IMU measurement residual}}}^{P _{b _{k+1}^{b _k}}:\text{Covariance from IMU pre-integration}} + \overbrace{\underbrace{\sum _{(l,j)\in\mathcal{C}} \lVert \mathbf{r} _\mathcal{C}(\hat{\mathbf{z}}^{c _j}, \mathcal{X}) {\lVert}^{2} _{P _l^{c _j}}} _{\text{Vision measurement residual}}}^{{P _l^{c _j}}:\text{Pixel reprojection covariance}} \right\rbrace \tag{1.2} $$

其中先验因子项参考²，IMU 测量残差项参考³，接下来的篇幅主要针对视觉残差项进行展开介绍。

2. 透视投影

计算视觉残差项涉及到许多多视几何等知识，相关参考⁴。在投影过程中，相机建立成何种模型往往需要根据实际使用的相机类型而定。这里不具体谈谈何种相机该如何建模，我们讨论更一般化的投影过程。将一个当前帧坐标系下的 3D 空间点：1. 投影到归一化平面（unit plane）；2. 投影到归一化球面（unit sphere）。下文中主要以特征点法 SLAM 的方式来定义投影残差形式。直接法 SLAM 的投影残差也仅仅是大同小异，利用链式法则在位置上加上一个灰度匹配块光度差值函数。

2.1 投影到归一化平面

这种方式最为常见，也相对简单，基本能够满足大多数情况。那么将一个当前帧坐标系下的 3D 空间点投影到归一化平面表示如下：

$$ z_{n,k} = h_p({}^{C_k}p_f) = \begin{bmatrix} C_x / C_z \newline C_y / C_z \end{bmatrix}, \ \text{where} \ {}^{C_k}p_f = \begin{bmatrix} C_x \newline C_y \newline C_z \end{bmatrix} \tag{2.1} $$

那么它的雅克比矩阵将通过如下计算可得：

$$ \frac{\partial h_p(\cdot)}{\partial {}^{C_k} p_f} = \begin{bmatrix} \frac{1}{C_z} & 0 & -\frac{C_x}{C_z^2} \newline 0 & \frac{1}{C_z} & -\frac{C_y}{C_z^2} \end{bmatrix} \tag{2.2} $$

在归一化平面上的残差定义也相对简单：$r_c(\hat{z} _{n,k}, \mathcal{X}) = \bar{z} _{n,k} - \check{z} _{n,k}$ ，其中 $\bar{z} _{n,k}$ 是二维测量在归一化平面的位置， $\check{z} _{n,k}$ 是预测特征在相机帧中归一化平面的位置。

2.2 投影到归一化球面

当相机的畸变特别大的时候（例如，鱼眼相机，环视相机等），投影到归一化平面的劣势将凸显出来。想象一下，在相同的位移下，相同的空间点如果投影到大畸变图像中心与边缘将会有不同的像素位移量。因此这个时候对于优化器来说特征点残差将具有不同的优化权重（如果不赋予不同信息矩阵的情况下），那么优化器就会变成有倾向性的，而非雨露均沾了。由此，我们定义另外一种投影模型，将一个当前帧坐标系下的 3D 空间点投影到归一化球面表示如下：

$$ \begin{align*} z_{n,k} &= h_p({}^{C_k}p_f) = \begin{bmatrix} C_x / \rho \newline C_y / \rho \newline C_z / \rho \end{bmatrix} \newline \text{where} \quad {}^{C_k}p_f &= \begin{bmatrix} C_x \newline C_y \newline C_z \end{bmatrix}, \rho = \lVert {}^{C_k}p_f \rVert = \sqrt{C_x^2 + C_y^2 +C_z^2} \end{align*} \tag{2.3} $$

那么它的雅克比矩阵将通过如下计算可得：

$$ \frac{\partial h_p(\cdot)}{\partial {}^{C_k} p_f} = \begin{bmatrix} \frac{1}{\rho} - \frac{C_x^2}{\rho^3} & -\frac{C_x C_y}{\rho^3} & -\frac{C_x C_z}{\rho^3} \newline -\frac{C_x C_y}{\rho^3} & \frac{1}{\rho} - \frac{C_y^2}{\rho^3} & -\frac{C_y C_z}{\rho^3} \newline -\frac{C_x C_y}{\rho^3} & -\frac{C_y C_z}{\rho^3} & \frac{1}{\rho} - \frac{C_z^2}{\rho^3} \end{bmatrix} \tag{2.4} $$

那么归一化球面的残差如何定义呢？这里参考¹中的方式。

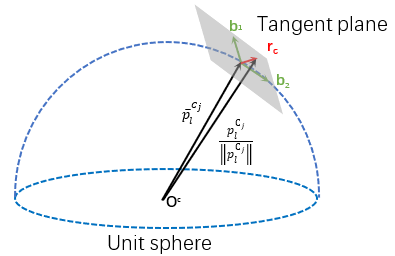
如上图所示，$\bar{p}_l^{c_j}$ 是二维测量在归一化球面的位置，$p_l^{c_j}$ 则是预测特征在相机坐标系的位置。$\mathbf{b}_1, \mathbf{b}_2$ 是以 $\overrightarrow{O^c\bar{p}_l^{c_j}}$ 为法向量，在点 $\bar{p}_l^{c_j}$ 处与归一化球面相切的平面内的两个正交单位向量。由此，重投影误差可以定义在切向平面上：

$$ r_c(\hat{z}_l^{c_j}, \mathcal{X}) = [\mathbf{b}_1 \ \ \ \mathbf{b}_2]^T (\bar{p}_l^{c_j} - \frac{p_l^{c_j}}{\lVert p_l^{c_j} \rVert}) \tag{2.5} $$

那么 $\mathbf{b}_1, \mathbf{b}_2$ 可以通过如下求解：

• 选择任意不平行于 $\bar{p}_l^{c_j}$ 的向量，例如 $[1 \ \ 0 \ \ 0]$
• 令 $\mathbf{b}_1 = \text{normalize}(\bar{p}_l^{c_j} \times [1 \ \ 0 \ \ 0])$
• 令 $\mathbf{b}_2 = \text{normalize}(\bar{p}_l^{c_j} \times \mathbf{b}_1)$

该方式的好处在于能够支持任意 FOV 的相机模型。

3. 特征点的表征

所谓特征点的表征（Point Feature Representations⁵）是指如何参数化从视觉图像中提取的 3D 特征点，不同的参数化过程最终的雅克比矩阵形式将有所不同。目前主要的参数化方式有：3D 位置 $(xyz)$ 和带方向角的逆深度。这两种方式都可以用在全局坐标系或者局部坐标系（anchor frame，锚坐标系），后者增加了对具有观察到特征点 “锚” 帧位恣的依赖。为了统一下文该小节中处理不同特征参数化 $\lambda$ ，我们详细推导了将不同表示映射到全局位置的通用函数 ${}^Gp_f = f(\cdot)$ 。

3.1 全局坐标系 XYZ

作为规范参数化，3D 点特征的全局位置由其在全局参考系中的 xyz 坐标简单地给出：

$$ {}^Gp_f = f(\lambda) = \begin{bmatrix} {}^Gx \newline {}^Gy \newline {}^Gz \end{bmatrix} ,\text{where} \ \ \lambda = {}^Gp_f = \begin{bmatrix} {}^Gx \newline {}^Gy \newline {}^Gz \end{bmatrix} \tag{3.1} $$

很明显，关于特征参数的雅克比矩阵是 $\frac{\partial f(\cdot)}{\partial \lambda} = I_{3\times3}$ 。

3.2 全局逆深度

3D 点特征的全局逆深度表示由下式给出（类似于球坐标）：

$$ {}^Gp_f = f(\lambda) = \frac{1}{\rho} \begin{bmatrix} \cos(\theta)\sin(\phi) \newline \sin(\theta)\sin(\phi) \newline \cos(\phi) \end{bmatrix} ,\text{where} \ \ \lambda = \begin{bmatrix} \theta \newline \phi \newline \rho \end{bmatrix} \tag{3.2} $$

关于特征参数的雅可比行列式可以计算为：

$$ \frac{\partial f(\cdot)}{\partial \lambda} = \begin{bmatrix} -\frac{1}{\rho}\sin(\theta)\sin(\phi) & \frac{1}{\rho}\cos(\theta)\cos(\phi) & -\frac{1}{\rho^2}\cos(\theta)\sin(\phi) \newline \frac{1}{\rho}\cos(\theta)\sin(\phi) & \frac{1}{\rho}\sin(\theta)\cos(\phi) & -\frac{1}{\rho}\cos(\theta)\sin(\phi) \newline 0 & -\frac{1}{\rho}\sin(\phi) & -\frac{1}{\rho^2}\cos(\phi) \end{bmatrix} \tag{3.3} $$

请注意，由于此表示在 z 距离变为零时具有奇异性，因此不建议在实践中使用。相反，应该使用 “锚坐标系” 反向深度（Anchored spherical Inverse Depth）表示（亦称为：局部球坐标逆深度加以区分）。如果特征在从它们看到的相机帧中表示（其中特征永远不应具有非正 z 方向），则锚定版本不存在此问题。

3.3 局部坐标系 XYZ

我们可以在某个“锚”帧（比如某个 IMU 局部帧，$\lbrace {}^{I_a} _GR, {}^Gp _{I_a} \rbrace$ ）中表示 3D 点特征，这通常是与检测到该特征的第一个相机帧相对应的 IMU 位姿。

$$ \begin{align*} {}^Gp _f &= f(\lambda, {}^{I_a} _GR, {}^Gp _{I _a}, {}^C _IR, {}^CP _I) \newline &= {}^{I _a} _GR^T {}^C _IR^T (\lambda - {}^CP _I) + {}^Gp _{I_a} \newline \text{wheel}\quad \lambda &= {}^{C_a}p_f = \begin{bmatrix} {}^{C_a}x & {}^{C_a}y & {}^{C_a}z \end{bmatrix}^T \end{align*} \tag{3.4} $$

关于特征状态的雅可比由下式给出:

$$ \frac{\partial f(\cdot)}{\partial \lambda} = {}^{I_a}_GR^T {}^C_IR^T \tag{3.5} $$

由于该表示中涉及到"锚"位姿，因此其雅可比矩阵计算为:

$$ \begin{align*} \frac{\partial f(\cdot)}{\partial {}^{I_a} _GR} &= -{}^{I_a} _GR^T \left \lfloor {}^C_IR^T ({}^{C_a}p_f - {}^CP_I) \times \right \rfloor \newline \frac{\partial f(\cdot)}{\partial {}^Gp _{I_a}} &= I _{3\times3} \end{align*} \tag{3.6} $$

此外，如果执行外参校准，还需要以下关于 IMU-Cam 外参的雅可比矩阵：

$$ \begin{align*} \frac{\partial f(\cdot)}{\partial {}^C_IR} &= -{}^{I_a}_GR^T {}^C_IR^T \left \lfloor ({}^{C_a}p_f - {}^CP_I) \times \right \rfloor \newline \frac{\partial f(\cdot)}{\partial {}^CP_I} &= -{}^{I_a}_GR^T {}^C_IR^T \end{align*} \tag{3.7} $$

3.4 局部球坐标逆深度

与全局逆深度情况类似，我们可以在锚坐标系 $\lbrace {}^{I_a} _GR, {}^Gp _{I_a} \rbrace$ 中使用带方位的逆深度（类似于球坐标）来表示 3D 点特征：

$$ \begin{align*} {}^Gp_f &= f(\lambda, {}^{I_a} _GR, {}^Gp _{I_a}, {}^C_IR, {}^CP_I) \newline &= {}^{I_a} _GR^T {}^C _IR^T ({}^{C_a}p_f - {}^CP_I) + {}^Gp _{I_a} \newline &= {}^{I_a} _GR^T {}^C _IR^T (\frac{1}{\rho} \begin{bmatrix} \cos(\theta)\sin(\phi) \newline \sin(\theta)\sin(\phi) \newline \cos(\phi) \end{bmatrix} - {}^CP _I) + {}^Gp _{I_a} \newline \text{wheel}\quad \lambda &= \begin{bmatrix} \theta & \phi & \rho \end{bmatrix}^T \end{align*} \tag{3.8} $$

关于特征参数的雅可比行列式可以计算为：

$$ \frac{\partial f(\cdot)}{\partial \lambda} = {}^{I_a}_GR^T {}^C_IR^T \begin{bmatrix} -\frac{1}{\rho}\sin(\theta)\sin(\phi) & \frac{1}{\rho}\cos(\theta)\cos(\phi) & -\frac{1}{\rho^2}\cos(\theta)\sin(\phi) \newline \frac{1}{\rho}\cos(\theta)\sin(\phi) & \frac{1}{\rho}\sin(\theta)\cos(\phi) & -\frac{1}{\rho}\cos(\theta)\sin(\phi) \newline 0 & -\frac{1}{\rho}\sin(\phi) & -\frac{1}{\rho^2}\cos(\phi) \end{bmatrix} \tag{3.9} $$

其他的雅克比计算与式 (3.5) 、式 (3.6) 相同。

3.5 局部逆深度（MSCKF⁶ 版本）

与 3.4 类似，将球坐标系改为归一化坐标系，则有：

$$ \begin{align*} {}^Gp_f &= f(\lambda, {}^{I_a} _GR, {}^Gp _{I_a}, {}^C_IR, {}^CP_I) \newline &= {}^{I_a} _GR^T {}^C_IR^T ({}^{C_a}p_f - {}^CP_I) + {}^Gp _{I_a} \newline &= {}^{I_a} _GR^T {}^C _IR^T (\frac{1}{\rho} \begin{bmatrix} \alpha \newline \beta \newline 1 \end{bmatrix} - {}^CP_I) + {}^Gp _{I_a} \newline \text{wheel}\quad \lambda &= \begin{bmatrix} \alpha & \beta & \rho \end{bmatrix}^T \end{align*} \tag{3.10} $$

关于特征参数的雅可比行列式可以计算为：

$$ \frac{\partial f(\cdot)}{\partial \lambda} = {}^{I_a}_GR^T {}^C_IR^T \begin{bmatrix} \frac{1}{\rho} & 0 & -\frac{1}{\rho^2}\alpha \ 0 & \frac{1}{\rho} & -\frac{1}{\rho^2}\beta \ 0 & 0 & -\frac{1}{\rho^2} \end{bmatrix} \tag{3.11} $$

其他的雅克比计算与式 (3.5) 、式 (3.6) 相同。

3.6 局部单一逆深度（VINS-Mono 版本）

该方式在 3.5 上在进一次简略，其中 $\hat{b}$ 为锚帧中提取特征的归一化坐标向量。

$$ \begin{align*} {}^Gp_f &= f(\lambda, {}^{I_a} _GR, {}^Gp _{I_a}, {}^C_IR, {}^CP_I) \newline &= {}^{I_a} _GR^T {}^C _IR^T ({}^{C_a}p_f - {}^CP_I) + {}^Gp _{I_a} \newline &= {}^{I_a} _GR^T {}^C _IR^T (\frac{1}{\rho} \hat{b} - {}^CP_I) + {}^Gp _{I_a} \newline \text{wheel}\quad \lambda &= \begin{bmatrix} \rho \end{bmatrix} \end{align*} \tag{3.12} $$

关于特征参数的雅可比行列式可以计算为：

$$ \frac{\partial f(\cdot)}{\partial \lambda} = - {}^{I_a}_GR^T {}^C_IR^T \frac{1}{\rho^2} \tag{3.13} $$

4. VINS-Fusion 中的视觉因子

4.1 视觉因子的残差求解

在 VINS-Fusion 中利用了一个 “UNIT_SPHERE_ERROR“ 宏定义来区别采用哪一种投影方式（在 2. 透视投影中介绍）。为了统一下文，下文将采用归一化平面的方式来进行推导。并且，特征点的参数化采用了 3.6 的方式。

在 VINS-Fusion 中定义了 3 中视觉重投影因子：1. 从第 i 帧左相机（或，主相机）投影到第 j 帧左相机 (对应代码中 projectionTwoFrameOneCamFactor)；2. 从第 i 帧左相机（或，主相机）投影到第 i 帧右相机 (或，从相机，对应代码 projectionOneFrameTwoCamFactor)；3. 从第 i 帧左相机（或，主相机）投影到第 j 帧右相机 (或，从相机，对应代码 projectionTwoFrameTwoCamFactor)。2/3 种投影因子仅在系统输入为双目时使用。我们主要推导第 1 种视觉重投影因子，其他的推导过程大同小异，就不再赘述。

• 视觉重投影约束：

  • 误差项 = 估计值 - 观测值

    • 观测值：第 j 帧相机，观测到路标点 $l$ 的像素坐标，转化到归一化系中，作为观测值；观测值是通过 LK 帧间跟踪得到
    • 估计值：将路标点 $l$ 从第 i 帧，投影到第 j 帧的归一化相机系中，计算得到的坐标为估计值

  • 优化变量：第 i 帧的位姿 $\lbrace {} _{b_i}^wR,{}^wp _{b_i}\rbrace$ 、第 j 帧的位姿 $\lbrace {} _{b_j}^wR,{}^wp _{b_j}\rbrace$ 、路标点 $l$ 的逆深度 $\lambda_l$ 、IMU-Cam 的外参 $\lbrace {}^{b} _cR,{}^bp_c, t_d \rbrace$

  • 协方差：像素误差 1.5 pixel

  

由此，重投影因子的残差可以定义如下：

$$ \mathbf{r} _\mathcal{C}(\hat{z} _l^{c_j}, \mathcal{X}) = \pi_c({} _c^bR^T ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR \frac{1}{\lambda_l} \pi_c^{-1}(\begin{bmatrix} {u} _l^{c_i} \newline {v} _l^{c_i} \end{bmatrix}) + {}^bp_c) + {}^wp _{b_i} - {}^wp _{b_j}) -{}^bp_c) ) - \begin{bmatrix} \hat{u} _l^{c_j} \newline \hat{v} _l^{c_j} \end{bmatrix} \tag{4.1} $$

其中，$\pi_c$ 为一个投影矩阵。如果采用 2.2 投影到归一化球面 的方式，那么对应有：

$$ \begin{align*} \bar{p} _l^{c_j} &= \pi_c^{-1}(\begin{bmatrix} \hat{u} _l^{c_j} \newline \hat{v} _l^{c_j} \end{bmatrix}) \newline p_l^{c_j} &= {} _c^bR^T ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR \frac{1}{\lambda_l} \pi_c^{-1}(\begin{bmatrix} {u} _l^{c_i} \newline {v} _l^{c_i} \end{bmatrix}) + {}^bp_c) + {}^wp _{b_i} - {}^wp _{b_j}) -{}^bp_c) \end{align*} \tag{4.2} $$

将式 (4.2) 代到式 (2.5) 就式一个完整的归一化球面残差求解了。

4.2 视觉因子中的雅克比求解

在求解雅克比过程中需要用到的公式、原理及推导可以参考⁷⁸⁹。设 $p_l^{c_i} = \frac{1}{\lambda_l} \pi_c^{-1}(\begin{bmatrix} {u}_l^{c_i} \newline {v}_l^{c_i} \end{bmatrix})$ 。

• 对第 i 帧的位姿 $\lbrace {} _{b_i}^wR,{}^wp _{b_i} \rbrace$ 求雅克比

  • 对 ${}^wp_{b_i}$ 求雅克比相对比较简单，利用链式法则如下所示。其中 $\frac{\partial \mathbf{r}_\mathcal{C}}{\partial p_l^{c_j}} = \begin{bmatrix} \frac{1}{C_z} & 0 & -\frac{C_x}{C_z^2} \newline 0 & \frac{1}{C_z} & -\frac{C_y}{C_z^2} \end{bmatrix}$ ，参考 2.1 投影到归一化平面 ，在下面的推导中将不再对该项进行展开。

  $$ \begin{align*} \frac{\partial \mathbf{r} _\mathcal{C}}{\partial {}^wp _{b_i}} &= \frac{\partial \mathbf{r} _\mathcal{C}}{\partial p_l^{c_j}} \frac{\partial p_l^{c_j}}{\partial {}^wp _{b_i}} \newline &= \begin{bmatrix} \frac{1}{C_z} & 0 & -\frac{C_x}{C_z^2} \newline 0 & \frac{1}{C_z} & -\frac{C_y}{C_z^2} \end{bmatrix} {} _c^bR^T {} _{b_j}^{w}R^T \end{align*} \tag{4.3} $$

  • 对 ${}_{b_i}^wR$ 求雅克比

  $$ \begin{align*} \frac{\partial \mathbf{r} _\mathcal{C}}{\partial {} _{b_i}^wR} &= \frac{\partial \mathbf{r} _\mathcal{C}}{\partial p_l^{c_j}} \frac{\partial p_l^{c_j}}{\partial {} _{b_i}^wR} \newline \text{(去掉无关项)其中有},\ \ \frac{\partial p_l^{c_j}}{\partial {} _{b_i}^wR} &= \lim _{\delta\theta \to 0} \frac{{} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR \exp(\lfloor \delta\theta \times \rfloor)({} _c^bR p_l^{c_i} + {}^bp _c) - {} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp _c)}{\delta\theta} \newline \text{利用} \exp(\lfloor \delta\theta \times \rfloor) \approx I+\lfloor \delta\theta \times \rfloor, \quad\quad\quad &\approx \lim _{\delta\theta \to 0} \frac{{} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR \lfloor \delta\theta \times \rfloor({} _c^bR p_l^{c_i} + {}^bp_c) }{\delta\theta} \newline \text{利用} \lfloor a \times \rfloor b = -\lfloor b \times \rfloor a, \quad\quad\quad &\approx \lim _{\delta\theta \to 0} \frac{-{} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR \lfloor ({} _c^bR p_l^{c_i} + {}^bp_c) \times \rfloor \delta\theta}{\delta\theta} \newline &\approx -{} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR \lfloor ({} _c^bR p_l^{c_i} + {}^bp_c) \times \rfloor \end{align*} \tag{4.4} $$

• 对第 j 帧的位姿 $\lbrace {}^{b_j} _wR,{}^wp _{b_j} \rbrace$ 求雅克比

  • 对 ${}^wp_{b_j}$ 求雅克比

  $$ \begin{align*} \frac{\partial \mathbf{r} _\mathcal{C}}{\partial {}^wp _{b_j}} &= \frac{\partial \mathbf{r} _\mathcal{C}}{\partial p_l^{c_j}} \frac{\partial p_l^{c_j}}{\partial {}^wp _{b_j}} \newline \text{有}, \ \ \frac{\partial p_l^{c_j}}{\partial {}^wp _{b_j}} &= - {} _c^bR^T {} _{b_j}^{w}R^T \end{align*} \tag{4.5} $$

  • 对 ${}_{b_j}^wR$ 求雅克比

  $$ \begin{align*} \frac{\partial \mathbf{r} _\mathcal{C}}{\partial {} _{b_i}^wR} &= \frac{\partial \mathbf{r} _\mathcal{C}}{\partial p_l^{c_j}} \frac{\partial p_l^{c_j}}{\partial {} _{b_i}^wR} \newline \text{有},\ \ \frac{\partial p_l^{c_j}}{\partial {} _{b_i}^wR} &= \lim _{\delta\theta \to 0} \frac{{} _c^bR^T ({} _{b_j}^{w}R\exp(\lfloor \delta\theta \times \rfloor))^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j}) - {} _c^bR^T {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j})}{\delta\theta} \newline &= \lim _{\delta\theta \to 0} \frac{{} _c^bR^T \exp(\lfloor \delta\theta \times \rfloor)^T {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j}) - {} _c^bR^T {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j})}{\delta\theta} \newline &= \lim _{\delta\theta \to 0} \frac{{} _c^bR^T \exp(\lfloor -\delta\theta \times \rfloor) {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j}) - {} _c^bR^T {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j})}{\delta\theta} \newline &\approx \lim _{\delta\theta \to 0} \frac{{} _c^bR^T (I- \lfloor \delta\theta \times \rfloor) {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j}) - {} _c^bR^T {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j})}{\delta\theta} \newline &\approx \lim _{\delta\theta \to 0} \frac{- {} _c^bR^T \lfloor \delta\theta \times \rfloor {} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j}) }{\delta\theta} \newline &\approx \lim _{\delta\theta \to 0} \frac{{} _c^bR^T \lfloor ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j}))\times \rfloor \delta\theta }{\delta\theta} \newline &\approx {} _c^bR^T \lfloor ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c)+ {}^wp _{b_i} - {}^wp _{b_j}))\times \rfloor \end{align*} \tag{4.6} $$

• 对路标点 $l$ 的逆深度 $\lambda_l$ 求雅克比

  $$ \begin{align*} \frac{\partial \mathbf{r}_\mathcal{C}}{\partial \lambda_l} &= \frac{\partial \mathbf{r} _\mathcal{C}}{\partial p_l^{c_j}} \frac{\partial p_l^{c_j}}{\partial \lambda_l} \newline \text{有}, \ \ \frac{\partial p_l^{c_j}}{\partial \lambda_l} &= - {} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \pi_c^{-1}(\begin{bmatrix} {u}_l^{c_i} \newline {v} _l^{c_i} \end{bmatrix}) \frac{1}{\lambda_l^2} \end{align*} \tag{4.7} $$

• 对 IMU-Cam 的外参 $\lbrace {}^{b}_cR,{}^bp_c, t_d \rbrace$ 求雅克比，当在线试试估计优化 IMU-Cam 外参时候

  • 对 ${}^bp_c$ 求雅克比

  $$ \begin{align*} \frac{\partial \mathbf{r} _\mathcal{C}}{\partial {}^bp_c} &= \frac{\partial \mathbf{r} _\mathcal{C}}{\partial p_l^{c_j}} \frac{\partial p_l^{c_j}}{\partial {}^bp_c} \newline \text{有}, \ \ \frac{\partial p_l^{c_j}}{\partial {}^bp_c} &= {} _c^bR^T ({} _{b_j}^{w}R^T {} _{b_i}^wR - I _{3\times3}) \end{align*} \tag{4.8} $$

  • 对 ${}^{b}_cR$ 求雅克比，稍微繁琐一些，但只需耐心一点求解就行

  $$ \begin{align*} \frac{\partial \mathbf{r} _\mathcal{C}}{\partial {} _{b_i}^wR} &= \frac{\partial \mathbf{r} _\mathcal{C}}{\partial p_l^{c_j}} \frac{\partial p_l^{c_j}}{\partial {} _{b_i}^wR} \newline \text{有},\ \ \frac{\partial p_l^{c_j}}{\partial {} _{b_i}^wR} &= \lim _{\delta\theta \to 0} \frac{({} _c^bR \exp(\lfloor \delta\theta \times \rfloor))^T ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR \exp(\lfloor \delta\theta \times \rfloor) p_l^{c_i} + {}^bp_c) + {}^wp _{b_i} - {}^wp _{b_j}) -{}^bp_c) - p_l^{c_j}}{\delta\theta} \newline \text{对分子进行化简有},&\simeq (I- \lfloor \delta\theta \times \rfloor)({} _c^bR^T ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR (I + \lfloor \delta\theta \times \rfloor) p_l^{c_i} + {}^bp_c) + {}^wp _{b_i} - {}^wp _{b_j}) -{}^bp_c)) - p_l^{c_j} \newline &\simeq (I- \lfloor \delta\theta \times \rfloor)({}_c^bR^T ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c) + {}^wp _{b_i} - {}^wp _{b_j}) -{}^bp_c) + {} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \lfloor \delta\theta \times \rfloor p_l^{c_i} ) - p_l^{c_j} \newline &\simeq (I- \lfloor \delta\theta \times \rfloor)(p_l^{c_j} + {} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \lfloor \delta\theta \times \rfloor p_l^{c_i} ) - p_l^{c_j} \newline \text{去掉二阶小量有}, &\simeq {} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \lfloor \delta\theta \times \rfloor p_l^{c_i} - \lfloor \delta\theta \times \rfloor p_l^{c_j} \newline &\simeq -{} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \lfloor p_l^{c_i} \times \rfloor \delta\theta + \lfloor p_l^{c_j} \times \rfloor \delta\theta \newline \text{得},\ \ \frac{\partial p_l^{c_j}}{\partial {} _{b_i}^wR} &\approx -{} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \lfloor p_l^{c_i} \times \rfloor + \lfloor p_l^{c_j} \times \rfloor \newline &\approx -{} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \lfloor p_l^{c_i} \times \rfloor + \lfloor ({} _c^bR^T ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR p_l^{c_i} + {}^bp_c) + {}^wp _{b_i} - {}^wp _{b_j}) -{}^bp_c) \times \rfloor \end{align*} \tag{4.9} $$

  • 对 $t_d$ 求雅克比，这部分需要做些稍微的变动，我们另起一个专题¹⁰来专门介绍。

Reference