Sliding Window & Marginalization Part-2

Sliding Window & Marginalization Part-1 该篇幅讲述了为何引入滑动窗口、并从概率的角度分析了从滑动窗口移除优化变量会引起协方差与信息矩阵怎么样的变化，最后介绍如何应用舒尔补来拆分并优雅的移除估计变量。有了先前的理论知识，接下来引进边缘化（Marginalization）与滑动窗口（Sliding Window）技术。

4. 滑动窗口算法

在 g2o ¹图优化中，通常把优化估计的变量称为顶点（圆圈表示），与优化变量之间构成的残差称为顶点连接的边（线、矩形）。下文中采用该方式进行构建因子图模型。

4.1 边缘化原理

参照²³，我们对边缘化的原理进行一个详尽的介绍。假设要 marginalize 掉的变量 $\mathbf{x}_m$ ，与该待 marg 掉变量有约束的变量用 $\mathbf{x}_b$ 表示，窗口中其他变量为 $\mathbf{x}_r$ ，即有 $\mathbf{x} = [\mathbf{x}_m, \mathbf{x}_b, \mathbf{x}_r]^T$ 。对应的测量约束为 $\mathbf{z} = { \mathbf{z}_b, \mathbf{z}_r } = { \mathbf{z}_m, \mathbf{z}_c, \mathbf{z}_r }$ ，其中 $\mathbf{z}_b = { \mathbf{z}_m, \mathbf{z}_c }$ 。为了助于理解，看下图所示：

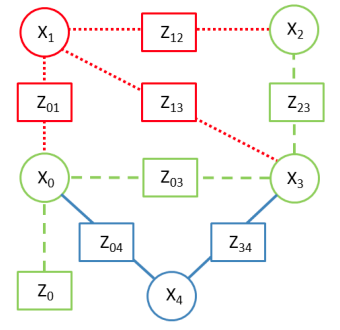
假设窗口中有 $\mathbf{x}_0,\mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_3,\mathbf{x}_4$ 五个状态，需要 marginalize 掉 $\mathbf{x}_1$ ， 而 $\mathbf{x}_0,\mathbf{x}_2,\mathbf{x}_3$ 和 $\mathbf{x}_1$ 有约束关系。因此，对应之前我们定义好的变量有 $\mathbf{x} _m =\mathbf{x} _1, \mathbf{x} _b=[\mathbf{x} _0,\mathbf{x} _2,\mathbf{x} _3]^T, \mathbf{x} _r=\mathbf{x} _4$ ，对应的约束为 $\mathbf{z}_m=\lbrace \mathbf{z} _{01},\mathbf{z} _{12},\mathbf{z} _{13}\rbrace,\mathbf{z} _c=\lbrace\mathbf{z} _{0},\mathbf{z} _{03},\mathbf{z} _{23}\rbrace, \mathbf{z} _r=\lbrace\mathbf{z} _{04},\mathbf{z} _{34}\rbrace$ 。

现在要丢掉变量 $\mathbf{x}_m$ ，而去优化 $\mathbf{x}_b$ 、$\mathbf{x}_r$ 。为了补丢失信息，正确的做饭是把 $\mathbf{x}_m$ 与 $\mathbf{x}_b$ 之间的约束 $\mathbf{z}_m$ 封存成状态 $\mathbf{x}_b$ 的先验信息。简言之，就是告诉 $\mathbf{x}_r$ ， $\mathbf{x}_m$ 和 $\mathbf{x}_b$ 之前是有约定的，不能只按照你的约定胡来。封存先验信息就是求在 $\mathbf{z}_m$ 条件下 $\mathbf{x}_b$ 的概率，公式如下： $$ p(\mathbf{x} _b \lvert \mathbf{z} _m) = \int _{\mathbf{x} _m} p(\mathbf{x} _b,\mathbf{x} _m \lvert \mathbf{z} _m)\mathrm{d}\mathbf{x} _m \doteq \mathcal{N}(\hat{\mathbf{x}} _b, \Lambda _t^{-1}) \tag{4.1} $$ 上式就是把 $\mathbf{x}_m$ 与 $\mathbf{x}_b$ 之间的约束封存成了 $\mathbf{x}_b \sim \mathcal{N}(\hat{\mathbf{x}}_b, \Lambda_t^{-1})$ 先验信息。带着先验信息去优化 $\mathbf{x}_b$ 、$\mathbf{x}_r$ 就不会损失约束信息了。

为了求解 $(\hat{\mathbf{x}} _b, \Lambda _t^{-1})$ ，我们需要求解：

$$ \lbrace \hat{\mathbf{x}} _b, \hat{\mathbf{x}} _m \rbrace = \arg\min _{\mathbf{x} _b, \mathbf{x} _m} \sum _{(i,j) \in \mathbf{z} _m} \frac{1}{2} \lVert \mathbf{z} _{ij} - h _{ij}(\mathbf{x} _i, \mathbf{x} _j) \lVert _{\Lambda _{ij}}^2 \tag{4.2} $$

在求解这个非线性最小二乘的时候，我们可以得到其信息（/Hessian）矩阵如下：

$$ H = \sum _{(i,j) \in \mathbf{z}_m} J _{ij}^T \Lambda _{ij} J _{ij} \doteq \begin{bmatrix} H _{mm} & H _{bm}^T \newline H _{bm} & H _{bb} \end{bmatrix} \tag{4.3} $$

一般情况，我们计算 $Hx = b$ 就能得到 $x$ ，然而在这里我们不需要计算 $\mathbf{x}_m$ ，因此可以对 $H$ 矩阵进行 Schur Complement 分解就能直接求解 $\mathbf{x}_b$ ：

$$ \begin{align*} \begin{bmatrix} H _{mm} & H _{bm}^T \newline H _{bm} & H _{bb} \end{bmatrix} \begin{bmatrix} \mathbf{x} _m \newline \mathbf{x} _b \end{bmatrix} &= \begin{bmatrix} \mathbf{b} _m \newline \mathbf{b} _b \end{bmatrix} \newline \begin{bmatrix} I & 0 \newline -H _{bm} H _{mm}^{-1} & I \end{bmatrix} \begin{bmatrix} H _{mm} & H _{bm}^T \newline H _{bm} & H _{bb} \end{bmatrix} \begin{bmatrix} \mathbf{x} _m \newline \mathbf{x}_b \end{bmatrix} &= \begin{bmatrix} I & 0 \newline -H _{bm} H _{mm}^{-1} & I \end{bmatrix} \begin{bmatrix} \mathbf{b} _m \newline \mathbf{b} _b \end{bmatrix} \newline \begin{bmatrix} H _{mm} & H _{bm}^T \newline 0 & H _{bb} - H _{bm} H _{mm}^{-1} H _{bm}^T \end{bmatrix} \begin{bmatrix} \mathbf{x} _m \newline \mathbf{x} _b \end{bmatrix} &= \begin{bmatrix} \mathbf{b}_m \newline \mathbf{b} _b - H _{bm} H _{mm}^{-1} \mathbf{b} _m \end{bmatrix} \end{align*} \tag{4.4} $$

根据上式易得：

$$ (H _{bb} - H _{bm} H _{mm}^{-1} H _{bm}^T) \hat{\mathbf{x}} _b = \mathbf{b} _b - H _{bm} H _{mm}^{-1} \mathbf{b} _m \tag{4.5} $$

因此我们即得到了 $\hat{\mathbf{x}} _b$ ，又得到了 $\Lambda _t = H _{bb} - H _{bm} H _{mm}^{-1} H _{bm}^T$ 。一旦这个先验信息得到确定，对于求解 $\mathbf{x}_m,\mathbf{x}_b,\mathbf{x}_r$ 全状态问题：

$$ \hat{\mathbf{x}} = \arg\min _{\mathbf{x}} \sum _{(i,j) \in \mathbf{z}} \frac{1}{2} \lVert \mathbf{z} _{ij} - h _{ij}(\mathbf{x} _i, \mathbf{x} _j) \lVert _{\Lambda _{ij}}^2 \tag{4.6} $$

就可以 marginalize 掉 $\mathbf{x}_m$ 而不损失信息：

$$ \hat{\mathbf{x}} = \arg\min _{\mathbf{x}} \lVert \hat{\mathbf{x}} _b - \mathbf{x} _b \lVert _{\Lambda_t}^2 + \sum _{(i,j) \in (\mathbf{x} _r, \mathbf{z} _c)} \lVert \mathbf{z} _{ij} - h _{ij}(\mathbf{x} _i, \mathbf{x} _j)) \lVert _{\Lambda _{ij}}^2 \tag{4.7} $$

由此给出了一个 Marginalization 引理（Lemma）：如果有一个局部最大似然估计（local-MLE (maximum likelihood estimation) [式 (4.2)]）有类似式 (4.3) 的测量雅克比 $J_{ij}$ 从而得到 $\Lambda_t = H_{bb} - H_{bm} H_{mm}^{-1} H_{bm}^T$ 这种形式的信息矩阵，那么边缘化非线性最小二乘（ marginalized-NLS (nonlinear least-squares)）问题（式 (4.7)）恰好近似于（up to second order/在二阶形式上）原来无边缘化的最大似然估计（式 (4.6)）。

关于该结论的证明，与之所以说恰好近似，而非等于的原因我们在 4.3 给出。在此之前，我们先来看个例子及其图形化描述。

4.2 图形化边缘化例子过程

4.2.1 样例 1

有如下最下二乘系统，

$$ \xi = \arg\min_\xi \frac{1}{2} \sum _i \lVert \mathbf{r} _i \lVert _{\Sigma _i}^2 ,\ \text{其中} \ \xi = \begin{bmatrix} \xi _1 \newline \xi _2 \newline \vdots \newline \xi _6 \end{bmatrix}, \mathbf{r} = \begin{bmatrix} \mathbf{r} _{12} \newline \mathbf{r} _{13} \newline \mathbf{r} _{14} \newline \mathbf{r} _{15} \newline \mathbf{r} _{56} \end{bmatrix} \tag{4.8} $$

对应的图模型如下图所示：

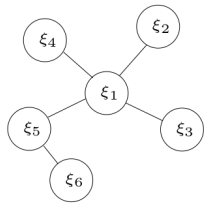
上诉最小二乘问题，对应五条边六个变量，最小化残差 $\mathbf{r}$ 优化 $\xi$ ，迭代求解为：

$$ \underbrace{ J^T \Sigma^{-1} J } _{H , \text{or} , \Lambda} \delta\xi = \underbrace{-J^T \Sigma^{-1} \mathbf{r}} _{\mathbf{b}} \tag{4.9} $$

注意，这里的 $\Lambda = \Sigma_{\text{new}}^{-1} \neq \Sigma^{-1}$ 反应的是求解的信息矩阵/方差，而 $\Sigma^{-1}$ 反应的是残差 $\mathbf{r}$ 的方差。另有，公式中的雅克比矩阵为： $$ J = \frac{\partial \mathbf{r}}{\partial \xi} = \begin{bmatrix} \frac{\partial \mathbf{r} _{12}}{\partial \xi} \newline \frac{\partial \mathbf{r} _{13}}{\partial \xi} \newline \frac{\partial \mathbf{r} _{14}}{\partial \xi} \newline \frac{\partial \mathbf{r} _{15}}{\partial \xi} \newline \frac{\partial \mathbf{r} _{56}}{\partial \xi} \end{bmatrix} \doteq \begin{bmatrix} J_1 \newline J_2 \newline J_3 \newline J_4 \newline J_5 \end{bmatrix}, J^T = \begin{bmatrix} J_1^T & J_2^T & J_3^T & J_4^T & J_5^T \end{bmatrix} \tag{4.10} $$

因为优化的变量是一致的，可以将五个增量方程写成连加：

$$ \sum_{i=1}^5 J_i^T \Sigma_i^{-1} J_i \delta\xi = - \sum_{i=1}^5 J_i^T \Sigma_i^{-1}\mathbf{r} \tag{4.11} $$

由于每个残差只和某几个状态量有关，因此，雅克比矩阵求导时，无关项的雅克比为 0。比如，

$$ \begin{align*} J_2 &= \frac{\partial \mathbf{r} _{13}}{\partial \xi} = \begin{bmatrix} \frac{\partial \mathbf{r} _{13}}{\partial \xi _1} & 0 & \frac{\partial \mathbf{r} _{13}}{\partial \xi _3} & 0 & 0 & 0 \end{bmatrix} \newline \Lambda _2 &= J _2^T \Sigma _2^{-1} J = \begin{bmatrix} (\frac{\partial \mathbf{r} _{13}}{\partial \xi _1})^T \Sigma _2^{-1} \frac{\partial \mathbf{r} _{13}}{\partial \xi _1} & 0 & (\frac{\partial \mathbf{r} _{13}}{\partial \xi _1})^T \Sigma _2^{-1} \frac{\partial \mathbf{r} _{13}}{\partial \xi _3} & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 & 0 \newline (\frac{\partial \mathbf{r} _{13}}{\partial \xi _3})^T \Sigma _2^{-1} \frac{\partial \mathbf{r} _{13}}{\partial \xi _1} & 0 & (\frac{\partial \mathbf{r} _{13}}{\partial \xi _3})^T \Sigma _2^{-1} \frac{\partial \mathbf{r} _{13}}{\partial \xi _3} & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{align*} \tag{4.12} $$

我们可以观测到雅克比矩阵与信息矩阵都具有稀疏性，同理，可以计算 $\Lambda_1, \Lambda_3, \Lambda_4, \Lambda_5$ ，并且也是稀疏的。将五个残差的信息矩阵加起来,得到样例最终的信息矩阵 $\Lambda$ ，可视化如下⁴:

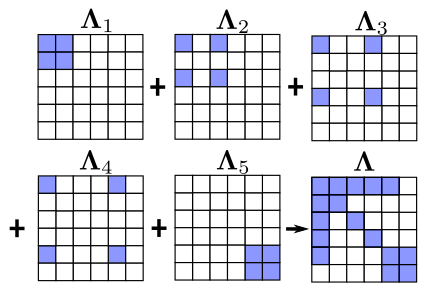
回忆先前的知识，直接丢弃变量和对应的测量值，会损失信息。正确的做法是使用边际概率，将丢弃变 量所携带的信息传递给剩余变量。对于上面这个样例，使用边际概率移除变量 $\xi_1$ ，信息矩阵的变化过程⁵为:

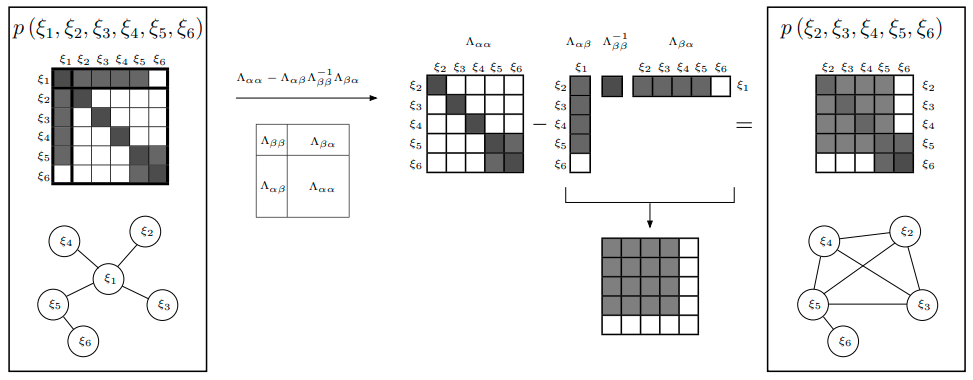
在这个 Marginalization 过程中，是否发现什么规律？

4.2.2 样例 2

不急，我们再看一个例子⁵，下图优化系统中，随着 $x_{t+1}$ 的引入，变量 $x_t$ 被移除：

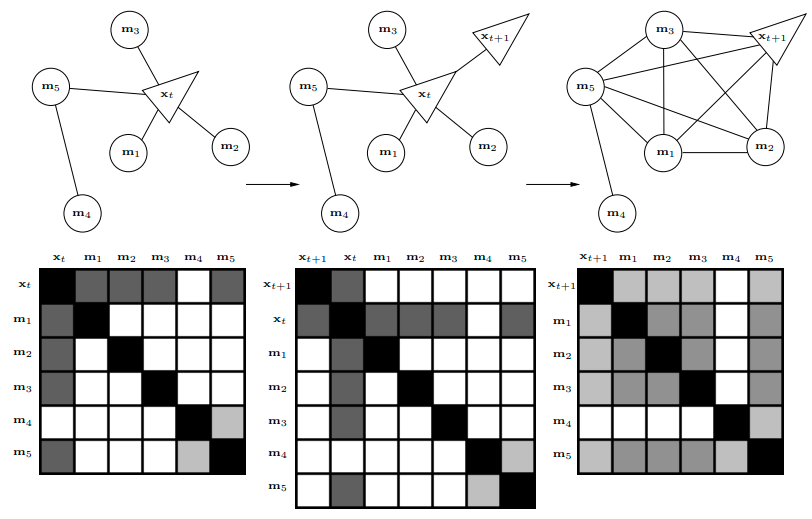
其中，第二步骤到第三步骤类似样例 1 中的操作过程，如下图所示（先变形，后计算）：

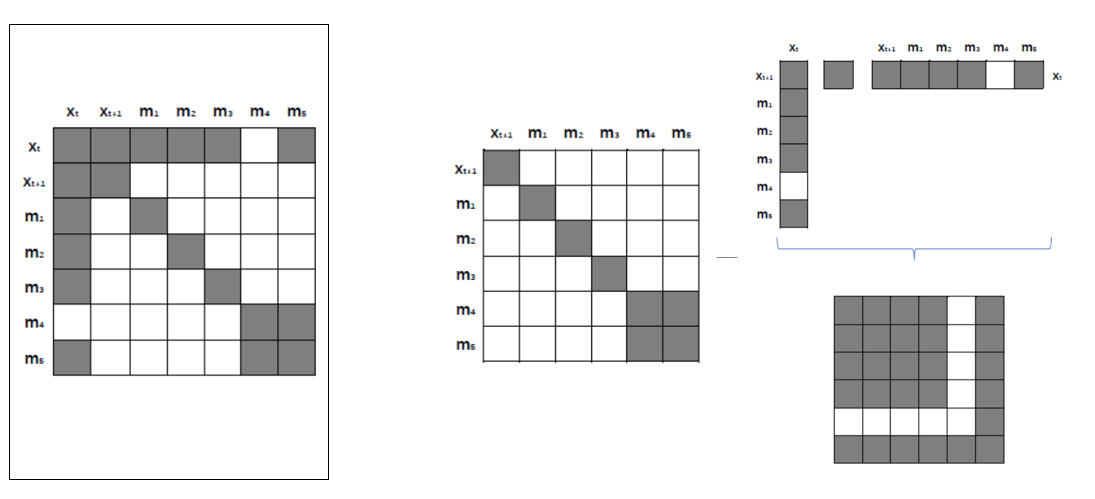
通过以上两个样例，我们观测到了 marginalization 会似的信息矩阵变稠密。换言之，原先条件独立的变量，可能变得相关，我们将这个过程称为 fill-in 。

4.3 滑动窗口中的 FEJ 算法

关于第一估计雅克比（FEJ, First Estimate Jacobians）先进行简单的描述。在 marginalize 的时候，求解滑动窗口估计器的迭代过程中，会不断迭代计算 $H$ 矩阵和残差 $b$ ，而在迭代过程中，状态变量会不断更新，计算雅克比的时候需要固定线性化点（fix the linearization point）。换言之，就是计算雅克比时候求导变量要固定，而不是用每一次迭代更新以后的状态量 $\mathbf{x}$ 去求雅克比。

在 4.1 中，给出了 marginalization 过程，承接先前的图模型，我们来证明先前给出的 Marginalization 引理，并从中说明为什么需要使用 FEJ 算法。

假设之前求最小二乘（式 (4.6)）的代价函数可以表达成：

$$ c(\mathbf{x}) = c_m(\mathbf{x}_m, \mathbf{x}_b) + c_r(\mathbf{x}_b, \mathbf{x}_r) \tag{4.13} $$

因此，我们就能得到，

$$ \min _\mathbf{x} c(\mathbf{x}) = \min _{\mathbf{x} _b, \mathbf{x} _r}(\min _{\mathbf{x} _m}c(\mathbf{x} _m, \mathbf{x} _b,\mathbf{x} _r)) = \min _{\mathbf{x} _b, \mathbf{x} _r}(c _r(\mathbf{x} _b, \mathbf{x} _r) + \min _{\mathbf{x} _m}c _m(\mathbf{x} _m, \mathbf{x} _b)) \tag{4.14} $$

求上面这个方程，我们可以先最小化 $c_m(\mathbf{x}_m, \mathbf{x}_b))$ ，注意这一步和我们求解现有信息是一样的，我们对他在最后值附近二阶泰勒展开得到：

$$ \begin{matrix} c _m(\mathbf{x} _m,\mathbf{x} _b) \simeq c _m(\hat{\mathbf{x}} _m,\hat{\mathbf{x}} _b) + g^T \begin{bmatrix} \mathbf{x} _m - \hat{\mathbf{x}} _m \newline \mathbf{x} _b - \hat{\mathbf{x}} _b \end{bmatrix} + \frac{1}{2} \begin{bmatrix} \mathbf{x} _m - \hat{\mathbf{x}} _m \newline \mathbf{x} _b - \hat{\mathbf{x}} _b \end{bmatrix}^T \Lambda \begin{bmatrix} \mathbf{x} _m - \hat{\mathbf{x}} _m \newline \mathbf{x} _b - \hat{\mathbf{x}} _b \end{bmatrix} \newline g = \begin{bmatrix} g _{mm} \newline g _{mb} \end{bmatrix} , \Lambda = \begin{bmatrix} \Lambda _{mm} & \Lambda _{mb} \newline \Lambda _{bm} & \Lambda _{bb} \end{bmatrix} \end{matrix} \tag{4.15} $$

其中，$g$ 和 $\Lambda$ 分别是雅克比和 Hessien 矩阵，需要注意的是求导变量（即线性化点）是 $\hat{\mathbf{x}}_m$ 和 $\hat{\mathbf{x}}_b$ 。我们还行希望 marginalize 掉 $\mathbf{x}_m$ ，注意到式 (4.15) 是个二次方程，该方程的最小值为在曲线的顶点处，因此 $\mathbf{x}_m$ 可以通过对式 (4.15) 求导等于 0 得到：

$$ \begin{align*} \frac{\partial c _m}{\partial \mathbf{x} _m} &= 0 + \begin{bmatrix} g _{mm} \newline g _{mb} \end{bmatrix}^T \begin{bmatrix} 1 \newline 0\end{bmatrix} + \begin{bmatrix} \Lambda _{mm} & \Lambda _{mb} \newline \Lambda _{bm} & \Lambda _{bb} \end{bmatrix} \begin{bmatrix} \mathbf{x} _m - \hat{\mathbf{x}} _m \newline \mathbf{x} _b - \hat{\mathbf{x}} _b \end{bmatrix} \begin{bmatrix} 1 \newline 0\end{bmatrix} \newline &=g _{mm} + \Lambda _{mm}(\mathbf{x} _m - \hat{\mathbf{x}} _m) + \Lambda _{bm}(\mathbf{x} _m - \hat{\mathbf{x}} _m) \newline \text{令} \quad \frac{\partial c _m}{\partial \mathbf{x} _m} &= 0 \newline \text{得} \quad \quad \mathbf{x} _m &= \hat{\mathbf{x}} _m - \Lambda _{mm}^{-1}(g _{mm}+\Lambda _{bm}(\mathbf{x} _b - \hat{\mathbf{x}} _b)) \end{align*} \tag{4.16} $$

把计算出来的 $\mathbf{x}_m$ 带入公式 (4.15) 得：

$$ \begin{align*} c_m(\mathbf{x} _m,\mathbf{x} _b) &\simeq c_m(\hat{\mathbf{x}} _m,\hat{\mathbf{x}} _b) + g^T \begin{bmatrix} \mathbf{x} _m - \hat{\mathbf{x}} _m \newline \mathbf{x} _b - \hat{\mathbf{x}} _b \end{bmatrix} + \frac{1}{2} \begin{bmatrix} \mathbf{x} _m - \hat{\mathbf{x}} _m \newline \mathbf{x} _b - \hat{\mathbf{x}} _b \end{bmatrix}^T \Lambda \begin{bmatrix} \mathbf{x} _m - \hat{\mathbf{x}} _m \newline \mathbf{x} _b - \hat{\mathbf{x}} _b \end{bmatrix} \newline \text{令}\quad \mathbf{x} _b - \hat{\mathbf{x}} _b = a \quad &\simeq c_m(\hat{\mathbf{x}} _m,\hat{\mathbf{x}} _b) + \newline &\quad \begin{bmatrix} g _{mm} \newline g _{mb} \end{bmatrix}^T \begin{bmatrix} - \Lambda _{mm}^{-1}(g _{mm}+\Lambda _{bm}a) \newline a \end{bmatrix} + \newline &\quad \frac{1}{2} \begin{bmatrix} - \Lambda _{mm}^{-1}(g _{mm}+\Lambda _{bm}a) \newline a \end{bmatrix}^T \begin{bmatrix} \Lambda _{mm} & \Lambda _{mb} \ \Lambda _{bm} & \Lambda _{bb} \end{bmatrix} \begin{bmatrix} - \Lambda _{mm}^{-1}(g _{mm}+\Lambda _{bm}a) \newline a \end{bmatrix} \newline &\simeq c_m(\hat{\mathbf{x}} _m,\hat{\mathbf{x}} _b) + \newline &\quad -g _{mm}^T \Lambda _{mm}^{-1}(g _{mm}+\Lambda _{bm} a) + g _{mb}^T a + \newline &\quad \frac{1}{2} \Big( (g _{mm}+\Lambda _{bm} a)^T \Lambda _{mm}^{-1} (g _{mm}+\Lambda _{bm} a) - a^T \Lambda _{bm}\Lambda _{mm}^{-1}(g _{mm}+\Lambda _{bm}a) \newline &\quad -(g _{mm}+\Lambda _{bm} a)^T \Lambda _{mm}^{-1} \Lambda _{mb} a + a^T \Lambda _{bb} a \Big) \newline \text{令常数项为}\ \xi\quad &\simeq \xi + (g _{mb} - \Lambda _{bm} \Lambda _{mm}^{-1} g _{mm})^T a + \frac{1}{2} a^T (\Lambda _{bb} - \Lambda _{bm} \Lambda _{mm}^{-1} \Lambda _{mb}) a \end{align*} \tag{4.17} $$

令 $g_t = g_{mb} - \Lambda_{bm} \Lambda_{mm}^{-1} g_{mm} \ ,\ \Lambda_t = \Lambda_{bb} - \Lambda_{bm} \Lambda_{mm}^{-1} \Lambda_{mb}$ 得：

$$ \min_{\mathbf{x}_m}c_m(\mathbf{x}_m,\mathbf{x}_b) \simeq \xi + g_t^T(\mathbf{x}_b - \hat{\mathbf{x}}_b) + \frac{1}{2} (\mathbf{x}_b - \hat{\mathbf{x}}_b)^T \Lambda_t (\mathbf{x}_b - \hat{\mathbf{x}}_b) \tag{4.18} $$

现在我们把代价函数 $c_m(\mathbf{x}_m, \mathbf{x}_b))$ 去掉 $\mathbf{x}_m$ 得到无信息损失的近似函数公式 (4.18) 代入式 (4.14) ，由此我们可以得到求解 $\mathbf{x}_m,\mathbf{x}_b,\mathbf{x}_r$ 全状态问题最大似然问题（式 (4.6)）近似等于下面求解下面式 (4.19) 代价函数的最小值：

$$ c’_r(\mathbf{x} _b, \mathbf{x} _r) = g_t^T(\mathbf{x} _b - \hat{\mathbf{x}} _b) + \frac{1}{2} (\mathbf{x} _b - \hat{\mathbf{x}} _b)^T \Lambda_t (\mathbf{x} _b - \hat{\mathbf{x}} _b) + \sum _{(i,j) \in (\mathbf{x} _r, \mathbf{z} _c)} \lVert \mathbf{z} _{ij} - h _{ij}(\mathbf{x} _i, \mathbf{x} _j)) \lVert _{\Lambda _{ij}}^2 \tag{4.19} $$

这里值得注意的是， $g_t$ 是式 (4.18) 近似损失函数的一阶导数，在求解 $\mathbf{x}_m$ 时候（式 (4.16)）令一阶导数为 0 ，所以在 $\hat{\mathbf{x}}_b$ 处有 $g_t = 0$ 。在最小化式 (4.19) 的迭代求解过程中，如果雅克比采用的是 marginalize 掉 $\mathbf{x}_m$ 时候的值，即对 $\mathbf{x}_b$ 求导采用的是 $\hat{\mathbf{x}}_b$ 去计算雅克比，那么此时公式 (4.19) 就等价于公式 (4.7) 。由此可以证明我们先前的推导是正确的。而如果我们采用的是和 $\mathbf{x}_r$ 一起优化后不断迭代得到的新 $\mathbf{x}_b$ 去计算雅克比，那么这时候 $g_t \neq 0$ 那么公式 (4.19) 相对于公式 (4.7) ，就引入了人为伪造的信息，系统就会不一致导致慢慢被破坏。这就是迭代优化过程中采用 FEJ 算法的原因。

4.4 FEJ 算法深入剖析

在 4.3 中，我们证明了边缘化的原理以及引入 FEJ 算法，下面篇幅中，我们通过图形化样例对 FEJ 进行深入剖析。回顾 4.2.1 样例1 ，并在原来移除变量 $\xi_1$ 后加入新的变量 $\xi_7$ 。将最基础的原始图模型结构展示如下：

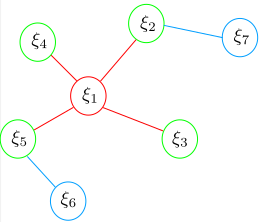
• 红色为被 marg 变量以及测量约束；绿色为跟 marg 变量有关的保留变量；蓝色为和 marg 变量无关的变量

1. 如上图所示，在 $t\in[0,k]$ 时刻，系统中有状态变量为 $\xi_i, i\in[1,6]$ 。第 $k’$ 时刻，加入新的观测和状态量 $\xi_7$
2. 在第 $k$ 时刻，最小二乘优化完以后，marg 掉变量 $\xi_1$ 。与 marg 量相关的变量为 $\xi_i, i \in [2,5]$ ，与 marg 无关的变量为 $\xi_6$
3. marg 发生以后， $\xi_1$ 变量以及对应的测量将被丢弃。同时，这部分信息通过 marg 操作传递给了保留变量
4. 在 $k’$ 时刻，加入新的状态量 $\xi_7$ 以及对应的观测，开始新一轮最小二乘优化。

新的变量 $\xi_7$ 跟老的变量 $\xi_2$ 之间存在观测信息，能构成残差 $\mathbf{r}_{27}$ 。marg 后的图模型如下所示。

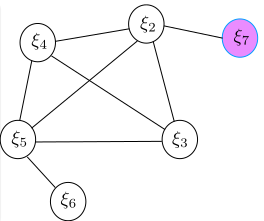
新的残差加上之前 marginalize 留下的信息，构成新的最小二乘系统，对应的信息矩阵的变化如下图所示：

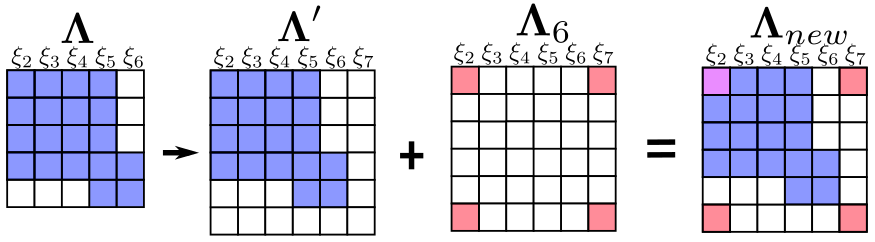
从中，注意到 $\xi_2$ 自身的信息矩阵由两部分组成，如果处理不当，这会使得系统存在潜在的风险。由于被 marg 的变量 $\xi_1$ 以及对应的测量被丢弃，先验信息中关于保留下来相关变量 $\xi_i, i \in [2,5]$ 的雅克比无法在后续求解中更新。但是变量 $\xi_i, i \in [2,5]$ 中部分变量还跟其他残差有联系，如 $\xi_2,\xi_5$ 。这些残差如 $\mathbf{r}_{27}$ 对于 $\xi_2$ 的雅克比会随着 $\xi_2$ 的迭代更新而不断在最新的线性化点处计算。而由于两部分计算雅克比时的线性化点不同，这可能会导致信息矩阵的零空间发生变化，从而在求解时引入错误信息。

例如：求解单目 SLAM 进行 Bundle Adjustment 优化时，问题对应的信息矩阵 $\Lambda$ 不满秩，对应的零空间为 $N$ 用高斯牛顿求解时有 $$ \begin{align*} \Lambda \delta \mathbf{x} &= \mathbf{b} \newline \Lambda \delta \mathbf{x} + N \delta \mathbf{x} &= \mathbf{b} \end{align*} \tag{4.20} $$ 增量 $\delta \mathbf{x}$ 在零空间维度下变化，并不会改变我们的残差。这意味着系统可以有多个满足最小化损失函数的解 $\mathbf{x}$ 。

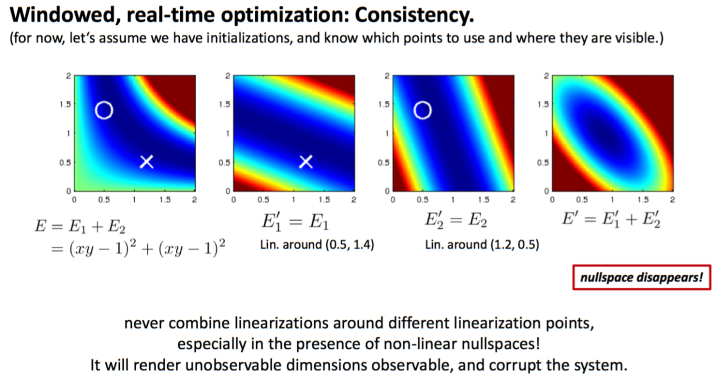
上图四张能量图中，第一张说明能量函数 $E$ 由两个相同的非线性函数 $E_1$ 和 $E_2$ 组成。令函数 $E = 0$ ，得到的解为 $xy = 1$ ，对应图中深蓝色的一条曲线。第二张能量图中的 $E’_1$ 是函数 $E_1$ 在点 $(0.5,1.4)$ 处的二阶泰勒展开，第三张能量图类似第二张，但是线性化点不同。最后一张图就是把第二、三两个近似能量图叠加起来对整个系统 $E$ 的近似。从中我们发现一个大问题，能量为 $0$ 的解由原来的一条曲线变成了一个点。多个解的问题，变成了一个确定解。不可观的变量，变成了可观的。

能观性⁶的一种定义：对于测量系统 $\mathbf{z} = h(\theta) + \eta$ ，其中 $\mathbf{z}\in \mathbb{R}^n$ 为测量值，$\theta \in \mathbb{R}^m$ 为系统状态量，$\eta$ 为测量噪声向量。$h(\cdot)$ 是个非线性函数，将状态量映射成测量量。对于理想数据，如果以下条件成立，则系统状态量 $\theta$ 可观。 $$ \forall \theta, \forall \theta’ \in \mathbb{R}^m,\lbrace \theta \neq \theta’ \rbrace \to \lbrace h(\theta) \neq h(\theta’) \rbrace \tag{4.21} $$ 对于 SLAM 系统而言（如单目 VO），当我们改变状态量时，测量不变意味着损失函数不会改变，更意味着求解最小二乘时对应的信息矩阵 $\Lambda$ 存在着零空间。单目 SLAM 系统 7 自由度不可观：6 自由度姿态 + 尺度。单目 + IMU 系统是 4 自由度不可观：yaw 角 + 3 自由度位置不可观。roll 和 pitch 由于重力的存在而可观，尺度因子由于加速度计的存在而可观。关于 FEJ 的其他解析可以参考⁷。

总结：滑动窗口算法中，对于同一个变量，不同残差对其计算雅克比矩阵时线性化点可能不一致，导致信息矩阵可以分成两部分，相当于在信息矩阵中多加了一些信息，使得其零空间出现了变化。而 FEJ 算法：不同残差对同一个状态求雅克比时，线性化点必须一致。这样就能避免零空间退化而使得不可观变量变得可观⁸。

Reference