Sliding Window & Marginalization Part-1
1. 为什么需要使用滑动窗口
在基于图优化的 SLAM 技术中,无论是 Pose-graph 和 Bundle Adjustment(下文简称 BA)其实都是最小二乘问题(如下), $$ \begin{align*} \mathrm{F}(\mathbf{x}) &= \sum_{\langle i,j \rangle \in \mathcal{c}} \underbrace{\mathrm{e} (\mathbf{x} _i, \mathbf{x} _j, \mathbf{z} _{ij})^T \mathbf{\Omega} _{ij} \mathrm{e}(\mathbf{x} _i, \mathbf{x} _j, \mathbf{z} _{ij})} _{\mathrm{ F _{ij}}} \newline \mathbf{x}^* &= \arg \min _\mathbf{x} \mathrm{F}(\mathbf{x}) \end{align*} \tag{1.1} $$ 然而,当待优化的位姿与特征点坐标增多时,最小二乘残差就会越来越多,信息矩阵也会越来越大,优化过程的计算量也会随着增大。因此不能无限制的添加代优化的变量,所以采用滑动窗口技术动态增加或移除优化变量,来限制计算量在一定的范围之内。
举个例子12,假设滑动窗口的固定大小为三个关键帧,一开始有三个关键帧 $kf_1$ 、$kf_2$ 、$kf_3$ 在窗口里,经过一段时间 $t$ , 第四个关键帧 $kf_4$ 加入优化,此时我们需要去掉 $kf_1$ ,只针对关键帧 $kf_2$ 、$kf_3$ 、$kf_4$ 进行优化。这样就能始终维持待优化变量的个数(或,维度),从而固定计算量。在上述的过程中,如果新关键帧到来时,我们直接丢弃关键帧 1 和关键帧 2、3 之间的约束,直接使用新关键 4 和 2、3 构建的约束来对窗口中的位姿进行新的优化,那么就有一个很自然的问题,优化后的 $kf_2$ 、$kf_3$ 的位姿与原来 $kf_1$ 的约束肯定就被破坏了,原来与 $kf_1$ 的一些约束信息就被损失了。那么应该如何做才能即使滑动窗口固定计算量又能充分保留信息呢?
为了更好的解释滑动窗口的原理与过程,我们从最基本的图优化 SLAM 概率建模开始,然后逐步分析当新优化变量加入时,如何优雅的去掉旧变量,在固定计算量的同时又能保留先前的约束信息并且不破坏系统的一致性。
2. 滑动窗口为什么不能直接去除元素
我们说直接去除滑动窗口中的待优化元素会丢失约束信息,那么我们从最基本的概率模型推导来证实这一结论。
2.1 SLAM 问题概率建模
假设某一机器人状态 $\xi$ 以及一次与该状态相关的观测 $r_i$ 。由于噪声的存在,观测服从概率分布表示为 $p(r_i|\xi)$ 。如果进行多次观测时,各个观测之间相互独立,那么多个观测 $r = (r_1, r_2, …,r_n)^T$ 构成的似然概率为: $$ p(r|\xi) = \prod_i p(r_i|\xi) \tag{2.1} $$ 如果知道机器人状态的先验信息 $p(\xi)$ ,如 GPS,车轮码盘信息等,则根据贝叶斯法则,可以求得后验概率: $$ p(\xi|r) = \frac{p(r|\xi)p(\xi)}{p(r)} \tag{2.2} $$ 通过最大后验估计,可以获取机器人系统的最有估计: $$ \xi_{\mathrm{MAP}} = \arg \max_\xi p(\xi|r) \tag{2.3} $$ 后验公式 (2.2) 中分母跟机器人系统状态量无关,因此直接舍弃,最大后验变成了: $$ \xi_\mathrm{MAP} = \arg\max_\xi \prod_i p(r_i|\xi) p(\xi) \tag{2.4} $$ 设概率服从高斯分布 $p(x) = \frac{1}{\sqrt{(2\pi)^N \det(\Sigma)}} \exp \left(-\frac{1}{2} (x-\mu)^T \Sigma^{-1}(x-\mu) \right)$ ,由于高斯分布中有 $\exp$ ,因此 (2.4) 等式后侧去对数 $\log$ ,根据对数的性质展开(舍弃系数),变成: $$ \xi_\mathrm{MAP} = \arg\min_\xi \left[-\sum_i \log p(r_i|\xi) - \log p(\xi) \right] \tag{2.5} $$ 更具体假设 $p(r_i|\xi) = \mathcal{N}(\mu_i, \Sigma_i),,, p(\xi) = \mathcal{N}(\mu_\xi, \Sigma_\xi)$ ,则有: $$ \xi_\mathrm{MAP} = \arg\min_\xi \sum_i | r_i - \mu_i |^2_{\Sigma_i} + | \xi - \mu_\xi |^2_{\Sigma_\xi} \tag{2.6} $$ 其中采用马氏距离(Mahalanobis distance)来叠加各项。上式 (2.6) 最小二乘的增量方程迭代求解: $$ J^T \Sigma^{-1} J \delta\xi = -J^T \Sigma^{-1}r \tag{2.7} $$ 从上面的过程我们可以看出,随着系统状态与观测的增多,计算量将变得越来越大。因此,我们期望去掉一些变量,从而保证系统的实时性。在引入边缘化移除滑动窗口待优化变量之前,我们先从概率上分析概率分布的协方差与信息矩阵。
2.2 协方差矩阵与信息矩阵
以下引入样例参考 David Mackay 的 The humble Gaussian distribution3 。
2.2.1 样例 1
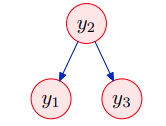
设 $y_2$ 为室外温度,$y_1$ ,$y_3$ 分别为房间 1 和房间 3 的室内温度,则有: $$ \begin{align*} y_2 &= v_2 \newline y_1 &= w_1 y_2 + v_1 \newline y_3 &= w_3 y_2 + v_3 \end{align*} \tag{2.8} $$ 其中,$v_i$ 相互独立,且各自服从协方差为 $\sigma^2_i$ 的高斯分布。从上述关系式 (2.7),根据协方差的计算方式,我们可以写出关于 $y$ 的协方差矩阵,先从对角元素开始计算: $$ \begin{align*} \Sigma_{11} &= \langle y_1 y_1 \rangle = \langle ({\color{red}{w_1}} {\color{green}{v_2}} + {\color{red}{v_1}})({\color{red}{w_1}} {\color{green}{v_2}} + {\color{red}{v_1}}) \rangle = {\color{red}{w_1^2}} \langle {\color{green}{v_2^2}} \rangle + 2{\color{red}{w_1}} \langle {\color{red}{v_1}} {\color{green}{v_2}} \rangle + \langle {\color{red}v_1^2} \rangle \newline &= {\color{red}w^2_1} {\color{green}\sigma_2^2} + {\color{red}\sigma_1^2} \end{align*} \tag{2.9} $$ 同理,有 $\Sigma_{22} = {\color{green}\sigma^2_2}$ ,$\Sigma_{33} = {\color{blue}w^2_3}{\color{green}\sigma^2_2} + {\color{blue}\sigma^2_3}$ 。对于协方差的非对角元素有: $$ \begin{align*} \Sigma_{12} &= \langle y_1 y_2 \rangle = \langle ({\color{red}{w_1}}{\color{green}{v_2}}) {\color{green}{v_2}} \rangle = {\color{red}{w_1}}{\color{green}{\sigma_2^2}} \newline \Sigma_{13} &= \langle y_1 y_3 \rangle = \langle ({\color{red}{w_1}}{\color{green}{v_2}} + {\color{red}v_1}) ({\color{blue}{w_3}}{\color{green}{v_2}} + {\color{blue}v_3}) \rangle = {\color{red}{w_1}}{\color{blue}{w_3}}{\color{green}{\sigma^2_2}} \end{align*} \tag{2.10} $$ 以此类推,可以得到整个协方差矩阵: $$ \Sigma = \begin{bmatrix} {\color{red}w^2_1} {\color{green}\sigma_2^2} + {\color{red}\sigma_1^2} & {\color{red}{w_1}}{\color{green}{\sigma_2^2}} & {\color{red}{w_1}}{\color{blue}{w_3}}{\color{green}{\sigma^2_2}} \newline {\color{red}{w_1}}{\color{green}{\sigma_2^2}} & {\color{green}\sigma^2_2} & {\color{blue}w_3}{\color{green}\sigma^2_2} \newline {\color{red}{w_1}}{\color{blue}{w_3}}{\color{green}{\sigma^2_2}} & {\color{blue}w_3}{\color{green}\sigma^2_2} & {\color{blue}w^2_3}{\color{green}\sigma^2_2} + {\color{blue}\sigma^2_3} \end{bmatrix} \tag{2.11} $$ 通过计算联合高斯分布从而得到协方差矩阵的逆: $$ \begin{align*} p(y_1, y_2, y_3) &= p(y_2) p(y_1|y_2) p(y_3|y_2) \newline &= {\color{green}\frac{1}{Z_2}\exp(-\frac{y_2^2}{2\sigma_2^2})} {\color{red}\frac{1}{Z_1}\exp(-\frac{(y_1 - w_1y_2)^2}{2\sigma_1^2})} {\color{blue}\frac{1}{Z_3}\exp(-\frac{(y_3 - w_3y_2)^2}{2\sigma_3^2})} \end{align*} \tag{2.12} $$ 利用指数性质求出联合概率分布: $$ \begin{align*} &p(y_1, y_2, y_3) \newline &= \frac{1}{Z} \exp( {\color{green}-\frac{y_2^2}{2\sigma_2^2}} {\color{red}-\frac{(y_1 - w_1y_2)^2}{2\sigma_1^2}} {\color{blue}-\frac{(y_3 - w_3y_2)^2}{2\sigma_3^2}} ) \newline &= \frac{1}{Z} \exp(-y_2^2 \left[ {\color{green}\frac{1}{2\sigma_2^2}} + {\color{red}\frac{w_1^2}{2\sigma_1^2}} + {\color{blue}\frac{w_3^2}{2\sigma_3^2}} \right] - y_1^2 {\color{red}\frac{1}{2\sigma_1^2}} + 2 y_1 y_2 {\color{red}\frac{w_1}{2\sigma_1^2}}-y_3^2 {\color{blue}\frac{1}{2\sigma_3^2}} + 2 y_3 y_2 {\color{blue}{\frac{w_3}{2\sigma_3^2}}}) \newline &= \frac{1}{Z} \exp(-\frac{1}{2} \begin{bmatrix} y_1 & y_2 & y_3 \end{bmatrix} \begin{bmatrix} {\color{red}\frac{1}{\sigma_1^2}} & {\color{red}-\frac{w_1}{\sigma_1^2}} & 0 \newline {\color{red}-\frac{w_1}{\sigma_1^2}} & {\color{red}\frac{w_1^2}{\sigma_1^2}} + {\color{green}\frac{1}{\sigma_2^2}} + {\color{blue}\frac{w_3^2}{\sigma_3^2}} & {\color{blue}{-\frac{w_3}{\sigma_3^2}}} \newline 0 & {\color{blue}{-\frac{w_3}{\sigma_3^2}}} & {\color{blue}\frac{1}{\sigma_3^2}} \end{bmatrix} \begin{bmatrix} y_1 \newline y_2 \newline y_3 \end{bmatrix}) \end{align*} \tag{2.13} $$ 由此可得协方差矩阵的逆,即信息矩阵(Information matrix): $$ \Lambda = \Sigma^{-1} = \begin{bmatrix} {\color{red}\frac{1}{\sigma_1^2}} & {\color{red}-\frac{w_1}{\sigma_1^2}} & 0 \newline {\color{red}-\frac{w_1}{\sigma_1^2}} & {\color{red}\frac{w_1^2}{\sigma_1^2}} + {\color{green}\frac{1}{\sigma_2^2}} + {\color{blue}\frac{w_3^2}{\sigma_3^2}} & {\color{blue}{-\frac{w_3}{\sigma_3^2}}} \newline 0 & {\color{blue}{-\frac{w_3}{\sigma_3^2}}} & {\color{blue}\frac{1}{\sigma_3^2}} \end{bmatrix} \tag{2.14} $$ 注意:信息矩阵中有两个元素为 0,它具体有什么含义呢。协方差逆矩阵中如果有坐标为 $(i,j)$ 的元素为 0,表示元素 $i$ 和 $j$ 关于其他变量条件独立,上面的例子中意味这变量 $y_1$ 和 $y_3$ 关于 $y_2$ 条件独立。
若室内外温度为正相关($w_i > 0$),
- 协方差矩阵中对角元素 $\Sigma_{ij}$ 表示两变量正相关;
- 信息矩阵中非对角元素为负数,设置为 0。$\Lambda_{12} < 0$ 表示在变量 $y_3$ 发生的前提下,元素 $y_1$ 和 $y_2$ 正相关。
2.2.2 样例 2
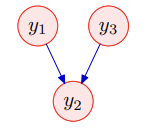
上图例如一个供暖费用计算过程,$y_2$ 表示多少钱每一个供暖时长,$y_1$ 表示煤炭价格,$y_3$ 表示天然气价格: $$ y_2 = w_1 y_1 + w_3 y_3 + v_2 \tag{2.15} $$ 同理,根据协方差矩阵的定义,我们可以得到协方差矩阵:(样例 2 中与样例 1 计算相似过程就略过了) $$ \Sigma = \begin{bmatrix} {\color{red} \sigma_1^2} & {\color{red} w_1\sigma_1^2} & 0 \newline {\color{red} w_1\sigma_1^2} & {\color{green}\sigma_2^2}+{\color{red}w_1^2\sigma_1^2} + {\color{blue}w_3^2\sigma_3^2} & {\color{blue}w_3\sigma_3^2} \newline 0 & {\color{blue}w_3\sigma_3^2} & {\color{blue}\sigma_3^2} \end{bmatrix} \tag{2.16} $$ 按照样例 1 中的方式,求协方差矩阵的逆: $$ \begin{align*} & p(y_1, y_2, y_3) = p(y_1) p(y_3) p(y_2|y_1, y_3) \newline &= {\color{red}\frac{1}{Z_1}\exp(-\frac{y_1^2}{2\sigma_1^2})} {\color{blue}\frac{1}{Z_3}\exp(-\frac{y_3^2}{2\sigma_3^2})} {\color{green}\frac{1}{Z_2}\exp(-\frac{(y_2-w_1 y_2-w_3 y_3)^2}{2\sigma_2^2})} \newline &= \frac{1}{Z}\exp({\color{red}-\frac{y_1^2}{2\sigma_1^2}} {\color{blue}-\frac{y_3^2}{2\sigma_3^2}} {\color{green}-\frac{(y_2-w_1 y_2-w_3 y_3)^2}{2\sigma_2^2}}) \newline &= \frac{1}{Z}\exp(\frac{1}{2} \begin{bmatrix} y_1 & y_2 & y_3 \end{bmatrix} \begin{bmatrix} {\color{red}\frac{1}{\sigma_1^2}} + {\color{green}\frac{w_1^2}{\sigma_2^2}} & {\color{green}-\frac{w_1}{\sigma_2^2}} & {\color{green}\frac{w_1 w_3}{\sigma_2^2}} \newline {\color{green}-\frac{w_1}{\sigma_2^2}} & {\color{green}\frac{1}{\sigma_2^2}} & {\color{green}-\frac{w_3}{\sigma_2^2}} \newline {\color{green}\frac{w_1 w_3}{\sigma_2^2}} & {\color{green}-\frac{w_3}{\sigma_2^2}} & {\color{blue}\frac{1}{\sigma_3^2}} + {\color{green}\frac{w_3^2}{\sigma_2^2}} \end{bmatrix} \begin{bmatrix} y_1 \newline y_2 \newline y_3 \end{bmatrix}) \end{align*} \tag{2.17} $$ 则有, $$ \Lambda = \Sigma^{-1} = \begin{bmatrix} {\color{red}\frac{1}{\sigma_1^2}} + {\color{green}\frac{w_1^2}{\sigma_2^2}} & {\color{green}-\frac{w_1}{\sigma_2^2}} & {\color{green}\frac{w_1 w_3}{\sigma_2^2}} \newline {\color{green}-\frac{w_1}{\sigma_2^2}} & {\color{green}\frac{1}{\sigma_2^2}} & {\color{green}-\frac{w_3}{\sigma_2^2}} \newline {\color{green}\frac{w_1 w_3}{\sigma_2^2}} & {\color{green}-\frac{w_3}{\sigma_2^2}} & {\color{blue}\frac{1}{\sigma_3^2}} + {\color{green}\frac{w_3^2}{\sigma_2^2}} \end{bmatrix} \tag{2.18} $$ 从上面推导出来的信息矩阵来看($w_i > 0$),
- 虽然 $y_1$ 和 $y_3$ 不相关,但是不能说明它们的信息矩阵对应元素 $\Lambda_{13}$ 为 0
- 恰恰信息矩阵中 $\Lambda_{13}>0$ ,表示的是在变量 $y_2$ 发生的条件下,变量 $y_1$ 和 $y_3$ 成负相关
- 对应上面的例子即为 $y_2$ 为常数,如果 $y_1$ 大,则 $y_3$ 小。
通过上述两个样例,非常有助于我们了解 SLAM 的信息矩阵 $\mathrm{H}$ 的组成。那么如果我们移除变量的话,那么信息矩阵与协方差矩阵是如何变化的呢?
2.2.3 样例 3 去除变量引发的变化
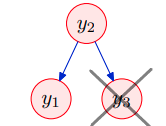
我们从样例 1 中去除变量 $y_3$ ,看看协方差矩阵与信息矩阵会发生什么变化。利用协方差的计算公式可知,$y_1, y_2$ 计算协方差时跟 $y_3$ 并无关系,所以 $$ \Sigma = \begin{bmatrix} {\color{red}w^2_1} {\color{green}\sigma_2^2} + {\color{red}\sigma_1^2} & {\color{red}{w_1}}{\color{green}{\sigma_2^2}} & \cancel{{\color{red}{w_1}}{\color{blue}{w_3}}{\color{green}{\sigma^2_2}}} \newline {\color{red}{w_1}}{\color{green}{\sigma_2^2}} & {\color{green}\sigma^2_2} & \cancel{{\color{blue}w_3}{\color{green}\sigma^2_2}} \newline \cancel{{\color{red}{w_1}}{\color{blue}{w_3}}{\color{green}{\sigma^2_2}}} & \cancel{{\color{blue}w_3}{\color{green}\sigma^2_2}} & \cancel{{\color{blue}w^2_3}{\color{green}\sigma^2_2} + {\color{blue}\sigma^2_3}} \end{bmatrix} \tag{2.19} $$ 就可以得到消去 $y_3$ 的协方差矩阵 $$ \Sigma’ = \begin{bmatrix} {\color{red}w^2_1} {\color{green}\sigma_2^2} + {\color{red}\sigma_1^2} & {\color{red}{w_1}}{\color{green}{\sigma_2^2}} \newline {\color{red}{w_1}}{\color{green}{\sigma_2^2}} & {\color{green}\sigma^2_2} \end{bmatrix} \tag{2.20} $$ 同样,我们只需要把信息矩阵中 $y_3$ 对应的部分($\color{blue}{蓝色}$)去掉就行: $$ \Lambda = \Sigma^{-1} = \begin{bmatrix} {\color{red}\frac{1}{\sigma_1^2}} & {\color{red}-\frac{w_1}{\sigma_1^2}} & \cancel{0} \newline {\color{red}-\frac{w_1}{\sigma_1^2}} & {\color{red}\frac{w_1^2}{\sigma_1^2}} + {\color{green}\frac{1}{\sigma_2^2}} + \cancel{{\color{blue}\frac{w_3^2}{\sigma_3^2}}} & \cancel{{\color{blue}{-\frac{w_3}{\sigma_3^2}}}} \newline \cancel{0} & \cancel{{\color{blue}{-\frac{w_3}{\sigma_3^2}}}} & \cancel{{\color{blue}\frac{1}{\sigma_3^2}}} \end{bmatrix} \tag{2.21} $$ 从而得到 $$ \Lambda’ = \Sigma’^{-1} = \begin{bmatrix} {\color{red}\frac{1}{\sigma_1^2}} & {\color{red}-\frac{w_1}{\sigma_1^2}} \ {\color{red}-\frac{w_1}{\sigma_1^2}} & {\color{red}\frac{w_1^2}{\sigma_1^2}} + {\color{green}\frac{1}{\sigma_2^2}} \end{bmatrix} \tag{2.22} $$ 可是实际情况下并不会把变量的项用颜色在矩阵中分类,所以引入边缘化(marginalization)和舒尔补(Schur’s complement)。
3. 舒尔补应用
首先,先给出舒尔补4的定义:给定任意的分块矩阵 $M$ ,如下所示, $$ M = \begin{bmatrix} A & B \newline C & D \end{bmatrix} \tag{3.1} $$
- 如果,矩阵块 $D$ 是可逆的,则 $A - BD^{-1}C$ 称之为 $D$ 关于 $M$ 的舒尔补
- 如果,矩阵块 $A$ 是可你的,则 $D - CA^{-1}B$ 称之为 $A$ 关于 $M$ 的舒尔补
更详尽的定义参见 wiki4
3.1 舒尔补的由来
将矩阵 $M$ 变成上三角或者下三角形过程中,都会遇到舒尔补: $$ \begin{align*} \begin{bmatrix} I & 0 \newline -CA^{-1} & I \end{bmatrix} \begin{bmatrix} A & B \newline C & D \end{bmatrix} &= \begin{bmatrix} A & B \ 0 & \Delta_A \end{bmatrix} \newline \begin{bmatrix} A & B \newline C & D \end{bmatrix} \begin{bmatrix} I & -A^{-1}B \newline 0 & I \end{bmatrix} &= \begin{bmatrix} A & 0 \ C & \Delta_A \end{bmatrix} \end{align*} \tag{3.2} $$ 其中,$\Delta_A = D-CA^{-1}B$ 。联合起来,将 $M$ 变成对角矩阵: $$ \begin{bmatrix} I & 0 \newline -CA^{-1} & I \end{bmatrix} \begin{bmatrix} A & B \newline C & D \end{bmatrix} \begin{bmatrix} I & -A^{-1}B \newline 0 & I \end{bmatrix} = \begin{bmatrix} A & 0 \newline 0 & \Delta_A \end{bmatrix} \tag{3.3} $$ 反过来,我们又能从对角形恢复成矩阵 $M$ : $$ \begin{bmatrix} I & 0 \newline CA^{-1} & I \end{bmatrix} \begin{bmatrix} A & 0 \newline 0 & \Delta_A \end{bmatrix} \begin{bmatrix} I & A^{-1}B \newline 0 & I \end{bmatrix} = \begin{bmatrix} A & B \newline C & D \end{bmatrix} \tag{3.4} $$ 舒尔补的好处在于可以可以快速的求解矩阵 $M$ 的逆: $$ \begin{bmatrix} A & B \newline C & D \end{bmatrix}^{-1} = \begin{bmatrix} I & -A^{-1}B \newline 0 & I \end{bmatrix} \begin{bmatrix} A^{-1} & 0 \newline 0 & \Delta_A^{-1} \end{bmatrix} \begin{bmatrix} I & 0 \newline -CA^{-1} & I \end{bmatrix} \tag{3.5} $$
3.2 舒尔补应用于多元高斯分布
假设一本多元变量 $\mathbf{x}$ 服从高斯分布,且由两部分组成:$\mathbf{x} = \begin{bmatrix} a \newline b \end{bmatrix}$ ,变量之间构成的协方差矩阵为 $K = \begin{bmatrix} A & C^T \newline C & D \end{bmatrix}$ ,其中 $A = \langle a, a \rangle, D = \langle b, b \rangle, C = \langle a, b \rangle$ 。由此变量 $\mathbf{x}$ 的概率分布为: $$ p(a,b) = p(a) p(b|a) \propto \exp(-\frac{1}{2} \begin{bmatrix} a \newline b \end{bmatrix}^T \begin{bmatrix} A & C^T \newline C & D \end{bmatrix}^{-1} \begin{bmatrix} a \newline b \end{bmatrix}) \tag{3.6} $$ 利用舒尔补公式 (3.5) ,对高斯分布进行分解,得5: $$ \begin{align*} & p(a, b) \newline & \propto \exp(-\frac{1}{2} \begin{bmatrix} a \newline b \end{bmatrix}^T \begin{bmatrix} A & C^T \newline C & D \end{bmatrix}^{-1} \begin{bmatrix} a \newline b \end{bmatrix}) \newline & \propto \exp(-\frac{1}{2} \begin{bmatrix} a \newline b \end{bmatrix}^T \begin{bmatrix} I & -A^{-1}C^T \newline 0 & I \end{bmatrix} \begin{bmatrix} A^{-1} & 0 \newline 0 & \Delta_A^{-1} \end{bmatrix} \begin{bmatrix} I & 0 \newline -CA^{-1} & I \end{bmatrix} \begin{bmatrix} a \newline b \end{bmatrix}) \newline & \propto \exp(-\frac{1}{2} \begin{bmatrix} a^T & (b-CA^{-1}a)^T \end{bmatrix} \begin{bmatrix} A^{-1} & 0 \newline 0 & \Delta_A^{-1} \end{bmatrix} \begin{bmatrix} a \newline b-CA^{-1}a \end{bmatrix}) \newline & \propto \exp \left(-\frac{1}{2}(a^T A^{-1}a) -\frac{1}{2}(b-CA^{-1}a)^T \Delta_A^{-1} (b-CA^{-1}a) \right) \newline & \propto \underbrace{\exp(-\frac{1}{2}a^T A^{-1}a)} _{p(a)} \underbrace{\exp\left( -\frac{1}{2}(b-CA^{-1}a)^T \Delta_A^{-1} (b-CA^{-1}a)\right)} _{p(b|a)} \end{align*} \tag{3.7} $$ 这意味着我们能从多元高斯分布 $p(a, b)$ 中分解得到边际概率 $p(a)$ 和条件概率 $p(b|a)$ 。从上式 (3.7) 可知,$p(a) \sim \mathcal{N}(0,A), p(b|a) \sim \mathcal{N}(CA^{-1}a, \Delta_A)$ 。即,边际概率的协方差直接取矩阵块就成,条件概率的协方差是 $a$ 对应的舒尔补,均值也变了。
因为基于优化的 SLAM 问题中,我们往往直接操作的是信息矩阵,而不是协方差矩阵。所以,有必要知道边际概率,条件概率的信息矩阵是何形式。
假设我们已知信息矩阵 $\Lambda$,利用公式 (3.5) 可得: $$ \begin{align*} \begin{bmatrix} A & B \newline C & D \end{bmatrix}^{-1} &= \begin{bmatrix} I & -A^{-1}B \newline 0 & I \end{bmatrix} \begin{bmatrix} A^{-1} & 0 \newline 0 & \Delta_A^{-1} \end{bmatrix} \begin{bmatrix} I & 0 \newline -CA^{-1} & I \end{bmatrix} \newline &= \begin{bmatrix} A^{-1}+A^{-1}C^T\Delta_A^{-1}CA^{-1} & -A^{-1}C^T\Delta_A^{-1} \newline -\Delta_A^{-1}CA^{-1} & \Delta_A^{-1} \end{bmatrix} \newline &\triangleq \begin{bmatrix} \Lambda_{aa} & \Lambda_{ab} \newline \Lambda_{ba} & \Lambda_{bb} \end{bmatrix} \end{align*} \tag{3.8} $$ 由此,可以总结得出 $p(a), p(b|a)$ 的信息矩阵:
- 边际概率 $p(a)$ 的协方差为 $A$ ,由式 (3.8) 易得信息矩阵为 $A^{-1} = \Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba}$ 。注意: $A^{-1}$ 是边际概率的信息矩阵,$\Lambda_{aa}$ 是联合分布信息矩阵的部分矩阵块
- 条件概率 $p(b|a)$ 协方差为 $\Delta_A$ ,由式 (3.8) 易得信息矩阵为 $\Delta_A^{-1} = \Lambda_{bb}$
3.3 舒尔补应用于多元高斯分布的结论验证
回顾 [2.2.3 样例 3 去除变量引发的变化](#2.2.3 样例3 去除变量引发的变化)中的操作,联合分布 $p(y_1, y_2, y_3)$ 的信息矩阵如下,
$$ \Lambda = \Sigma^{-1} = \left[ \begin{array}{c|c} \overbrace{\begin{matrix} {\color{red}\frac{1}{\sigma _1^2}} & {\color{red}-\frac{w _1}{\sigma _1^2}} \newline {\color{red}-\frac{w _1}{\sigma _1^2}} & {\color{red}\frac{w _1^2}{\sigma _1^2}} + {\color{green}\frac{1}{\sigma _2^2}} + {\color{blue}\frac{w _3^2}{\sigma _3^2}} \end{matrix}}^{\Lambda _{aa}} & \overbrace{\begin{matrix} 0 \newline {\color{blue}{-\frac{w _3}{\sigma _3^2}}} \end{matrix}}^{\Lambda _{ab}} \newline \hline \underbrace{\begin{matrix} 0 \ \ \ \ \ \ \ \ \ \ & {\color{blue}{-\frac{w _3}{\sigma _3^2}}} \ \ \ \ \end{matrix}} _{\Lambda _{ba}} & \underbrace{{\color{blue}\frac{1}{\sigma _3^2}}} _{\Lambda _{bb}} \end{array} \right] \tag{3.9} $$
从联合分布 $p(y_1, y_2, y_3)$ 中 marg 掉变量 $y_3$ ,即 $p(y_1, y_2)$ 对应的信息矩阵可以用 $A^{-1} = \Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba}$ 得到:
$$ \begin{align*} \Lambda’ = \Sigma’^{-1} &= \Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba} \newline &= \Lambda_{aa} - \begin{bmatrix} 0 \newline -\frac{w_3}{\sigma_3^2} \end{bmatrix} \sigma_3^2 \begin{bmatrix} 0 & -\frac{w_3}{\sigma_3^2} \end{bmatrix} \newline &= \Lambda_{aa} - \begin{bmatrix} 0 & 0 \newline 0 & \frac{w_3^2}{\sigma_3^2} \end{bmatrix} \newline &= \begin{bmatrix} {\color{red}\frac{1}{\sigma_1^2}} & {\color{red}-\frac{w_1}{\sigma_1^2}} \newline {\color{red}-\frac{w_1}{\sigma_1^2}} & {\color{red}\frac{w_1^2}{\sigma_1^2}} + {\color{green}\frac{1}{\sigma_2^2}} \end{bmatrix} \end{align*} \tag{3.10} $$ 得到的结果与去掉($\color{blue}{蓝色}$)得到的结果完全以致,即得证。
3.4 总结
边际概率对于协方差矩阵的操作是很容易的,但不好操作信息矩阵。条件概率恰好相反,对于信息矩阵容易操作,不好操作协方差矩阵。表格总结如下6 $$ p(a,b) = \mathcal{N}\left(\begin{bmatrix} \mu_a \newline \mu_b \end{bmatrix}, \begin{bmatrix} \Sigma_{aa} & \Sigma_{ab} \newline \Sigma_{ba} & \Sigma_{bb} \end{bmatrix}\right) = \mathcal{N}^{-1}\left(\begin{bmatrix} \eta_a \newline \eta_b \end{bmatrix}, \begin{bmatrix} \Lambda_{aa} & \Lambda_{ab} \newline \Lambda_{ba} & \Lambda_{bb} \end{bmatrix}\right) $$
| 边际概率 $p(a) = \int p(a, b)\mathrm{d}b$ | 条件概率 $p(a \lvert b) = p(a,b)/p(b)$ | |
|---|---|---|
| 协方差矩阵 | $\begin{align*} \mu &= \mu_a \newline \Sigma &= \Sigma_{aa} \end{align*}$ | $\begin{align*} \mu’ &= \mu_a + \Sigma_{ab}\Sigma_{bb}^{-1}(b-\mu_b) \newline \Sigma’ &= \Sigma_{aa} - \Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba} \end{align*}$ |
| 信息矩阵 | $\begin{align*} \eta &= \eta_a - \Lambda_{ab}\Lambda_{bb}^{-1}\eta_b \newline \Lambda &= \Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba} \end{align*}$ | $\begin{align*} \eta’ &= \eta_a - \Lambda_{ab}b \newline \Lambda’ &= \Lambda_{aa} \end{align*}$ |
Reference
白巧克力亦唯心: DSO 中的Windowed Optimization、 SLAM中的marginalization 和 Schur complement ↩︎
高翔、贺一家:手写 VIO ↩︎
David Mackay. The humble Gaussian distribution. In:(2006) ↩︎
Huang. Conditional and marginal distributions of a multivariate Gaussian ↩︎
Matthew R Walter, Ryan M Eustice, and John J Leonard. “Exactly sparse extended information filters for feature-based SLAM ↩︎