平面透射 - Planar Homology

Planar Homology

如果平面射影变换 $H$ 具有一条由固定点（称为轴）组成的线，以及不在该线上的固定点（称为顶点），则该平面射影变换 H 是平面透射 (planar homology) ^{1 2}，见 Fig. 1 。从代数角度来看，该矩阵具有两个相等和另一个不同的特征值，并且与相等特征值对应的特征空间是二维的。其轴是穿过横跨该特征空间的两个特征向量（即点）的直线。顶点对应于另一个特征向量。 不同特征值与重复特征值的比率是透射的特征不变量 $\mu$（即不计比例因子的区别，其特征值是 $\lbrace \mu, 1, 1\rbrace$ ）。

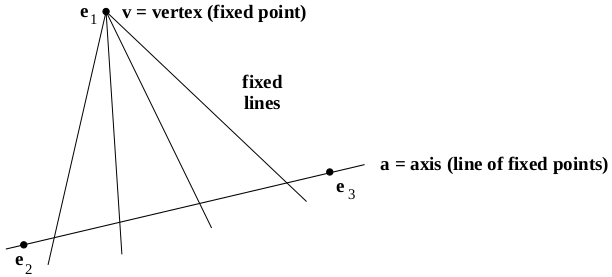
Fig. 1: 平面透射是一种平面射影变换，它具有一条由固定点组成的线（称为轴）$\bf a$ 和一个不在直线上的独立固定点 $\bf v$（称为透射的中心或顶点）。存在过顶点的一束不动线。在代数上，变换矩阵的两个特征值相等（图中重复的特征值是 $\lambda_2$ 和 $\lambda_3$ ），而不动直线与矩阵的二维不变空间对应。

平面透射的性质包括：

• 连接对应点的直线相交于顶点，对应直线（即通过两对对应点的直线）相交于轴。这是笛沙格定理 (Desargues’ Theorem) 的一个例子。见 Fig. 2-a 。
• 由顶点、一组对应点以及连接这些点的直线与不动点的直线的交点定义的交比对所有与该透射相关的点都是相同的。 见图 Fig. 2-b 。
• 对于由一个平面透射关联的曲线，对应切线（定义相应线的邻点的极限）在轴上相交。
• 顶点 (2 dof)、轴 (2 dof) 和不变量交比 (1 dof) 足以完全定义透射。 因此，平面透射有 5 个自由度。
• 3 个匹配点足以计算一个平面透射。 这些点匹配的 6 个自由度过度约束了 5 个自由度的透射。

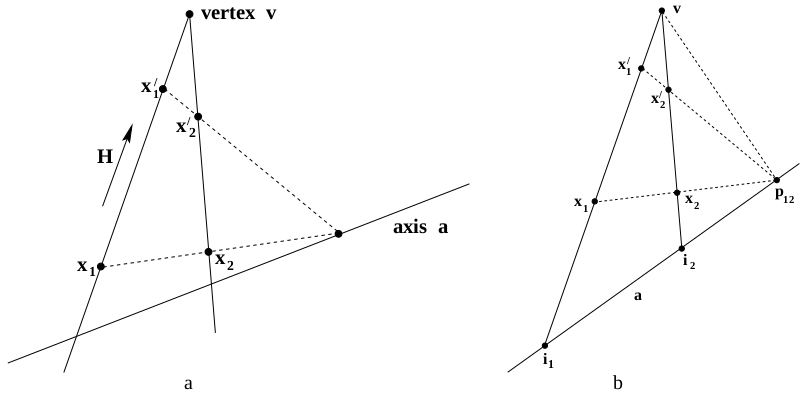
Fig. 2: 透射变换。(a) 在此变换下，轴上的点被映射到自身；轴外的每个点都位于过 $\bf v$ 并与 $\bf a$ 相交于一条不动线上，且被映射到此直线上的另一个点。因此，对应点对 $\mathbf x \leftrightarrow \mathbf x’$ 与透射顶点共线。对应线（即过对应点对的线）在轴上相交：例如，线 $\langle \mathbf x_1, \mathbf x_2 \rangle$ 和 $\langle \mathbf x_1’, \mathbf x_2’ \rangle$ 。(b) 由顶点 $\bf v$ 、对应点 $\bf x$、$\bf x’$ 以及它们与轴的交点 $\bf i$ 定义的交比是透射的特征不变量，并且对于所有对应点取值都是相同的。例如，四个点 $\lbrace \mathbf v,\mathbf x_1’,\mathbf x_1, \mathbf i_1 \rbrace$ 和 $\lbrace \mathbf v,\mathbf x_2’,\mathbf x_2, \mathbf i_2 \rbrace$ 的交比相等，因为它们通过共点于 $\mathbf p_{12}$ 的直线透射相关。 由此可见，透射相关的所有点的交比是相同的。

平面透射自然发生于用 3 空间透视变换相关联的两个平面的图像中（即，连接两个平面上对应点的直线交于一点）。 一个例子是平面物体的图像与其平面上的阴影图像之间的变换。在这种情况下，轴是两个平面交线的成像，顶点是光源的成像，见 Fig. 3 。

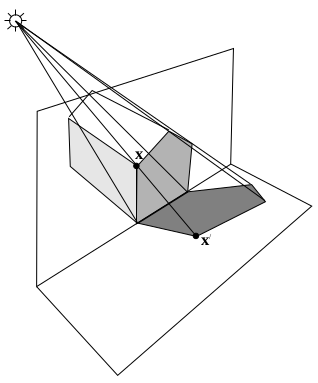
Fig. 3: 一个平面（建筑物的端面）的图像与其在另一个平面（地面）上的阴影图像之间的射影变换。

参数化：表示透射的射影变换可以直接用表示轴 $\bf a$ 和顶点 $\bf v$ 的 3 维向量以及特征比率 $\mu$ 来参数化，即， $$ H = I + (\mu - 1) \cfrac{\bf va^\top}{\bf v^\top a} \tag{1} \label{1} $$ 其中，$I$ 是单位矩阵，可以验证它的逆变换由下式给出 $$ H^{-1} = I + \bigg(\frac1\mu - 1 \bigg) \cfrac{\bf va^\top}{\bf v^\top a} \tag{2} \label{2} $$ 其特征向量是 $\lbrace \mathbf e_1 = \mathbf v, \mathbf e_2 = \mathbf a_1^\bot, \mathbf e_3 = \mathbf a_2^\bot\rbrace$ ，对应的特征值为 $\lbrace \lambda_1 = \mu, \lambda_2 = 1, \lambda_3 = 1 \rbrace$ 。其中，$\mathbf a_i^\bot$ 是生成与 3 为向量 $\bf a$ 正交的空间的两个向量，即 $\mathbf a^\top \mathbf a_i^\bot = 0$ 和 $\mathbf a = \mathbf a_1^\bot \times \mathbf a_2^\bot$ 。如果轴或顶点在无穷远，从代数上说，如果 $\mathbf a = (0, 0, 1)^\top$ ，那么轴在无穷远；或如果 $\mathbf v = (v_1, v_2, 0)^\top$ ，那么顶点在无穷远；并且在这两种情况下变换矩阵 $H$ 的最后一行都是 $(0, 0, 1)$ 。

一个构成平面透射的实用示例（被用在散斑投射器与相机的标定上³），

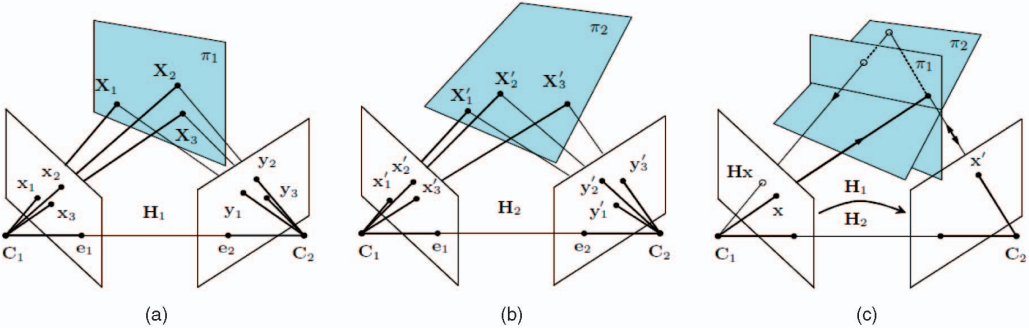
Fig. 4: ⁴由移动的三元组点引起的单应性。 假设三个 3D 点 $\lbrace X_i \rbrace \to \lbrace X_i’ \rbrace$ 的运动被两台静止摄像机 $C_1$ 和 $C_2$ 观察到，即 $\lbrace \mathrm x_i\rbrace \to \lbrace \mathrm x_i’\rbrace$ 和 $\lbrace \mathrm y_i\rbrace \to \lbrace \mathrm y_i’\rbrace$ 。与极点 $\mathrm e_1 \leftrightarrow \mathrm e_2$ 一起，点对应关系 $\mathrm x_i \leftrightarrow \mathrm y_i$ 和 $\mathrm x_i’ \leftrightarrow \mathrm y_i’$ 产生了从左视图到右视图的两个单应性 $H_1$ 和 $H_2$ 。将左视图映射到自身的单应性被定义为 $H = H_2^{-1} H_1$ 。对于三联体的相似运动，该单应性被证明是透射，因此具有两个相同的特征值，从而为识别相似的姿势转换提供了约束。

Reference