Online Photometric Calibration

在「光度标定」文章中，介绍了一种用于离线非参数化标定相机光度的方式。然而，目前现有的大多数据集或使用未知相机获取的图像视频系列，往往都是自动曝光且曝光时间未知的，并且曝光不受用户控制。因此，当我们希望在没有提供光度校准和没有提供相机访问控制的数据集上运行基于直接法的视觉里程计系统时，希望有一种有效的在线实时校准光度参数的方式。因此，Paul Bergmann, Rui Wang, and Daniel Cremers 提出了针对于自动曝光图像视频序列用于实时视觉里程计和 SLAM 的在线光度校准¹。

1. 光度成像过程

在「光度标定-1. 相机成像原理」和「光度标定-2. 相机光度模型」中，我们已经详细介绍了光度成像过程与如何进行模型化。但为了篇幅的完整性，这里还是将论文¹中的内容进行描述介绍。

场景点被光源照亮，并将光线反射回空间。反射的光量称为场景点的辐射度 (radiance) $L$。如果一个移动的观察者接收到的辐亮度与观察者的观看角度无关，则称场景点表现出朗伯反射行为。场景点的辐射亮度被相机的传感器元件捕获。在传感器位置 $x$ 处接收到的总能量称为辐照度 (Irradiance) $I(x)$。

我们通常期望且假设在不同空间位置具有相同辐射度的场景点会产生相同的传感器辐照度。然而，对于大多数相机，可以在图像边界观察到像素强度的辐照度衰减。这种所谓的渐晕效应 (vignetting effect) 可能是由于镜筒对光线的部分阻挡，也可能是由镜头几何形状引起的。因此，辐照度 $I(x)$ 可以通过将场景点的辐射度与渐晕因子 $V: \Omega \to [0, 1]$ 相乘得到，这取决于图像传感器的空间位置 $x \in \Omega$ ， $$ I(x) = V(x) L \tag{1.1}\label{1.1} $$ 当拍摄图像时，传感器辐照度在由相机曝光时间 $e$ 指定的时间窗口内进行积分。假设传感器单元的辐照度在此窗口内是恒定的。由此，累积的辐照度值以 $I_{acc}(x) = e I(x)$ 的形式给出。

$I_{acc}(x)$ 然后被相机相应函数 (CRF, camera response function) $f : {\mathbb R} \to [0, 255]$ 映射到一个图像输出强度。对于真实的相机，CRF 的输入受到相机动态范围限制。如果累积辐照度落在相机动态范围之外，即场景曝光不足或过度，将分别被赋予像素值 0 或 255 。在实际工程应用代码中，由于无法恢复辐射度的物理尺度，所以将相机的动态范围归一化为单位区间 $[0,1]$ 。

将场景点辐射度 $L$ 映射到图像输出强度 $O$ 的整个图像形成过程可以简洁地模型化为： $$ O = f( e V(x) L ) \tag{1.2}\label{1.2} $$

2. 跟踪前端

给定一组用于校准的图像帧 $F$ ，等式 $\eqref{1.2}$ 中除了输出强度 $O$ 之外的所有变量都是先验未知的。为了获取光度校准，必须旋转一组场景点 $P$ ，并且必须估计它们在可见图像上的投影。作者使用在金字塔处理的图像上进行 KLT 特征跟踪来实现获得点对应关系。工程上采用了非标准的 KLT 跟踪器² ，可以使用 Schur 补有效地联合优化跟踪和帧之间的增益比，从而提高针对图像之间有强烈曝光变化的鲁棒性。下图显示了应用在曝光变化较大的帧上时两种标准 KLT 跟踪器与自适应 KLT 跟踪器的差异，图中，上一行：两幅图像之间采用标准 KLT；下一行两幅图之间采用自适应 KLT，角点提取采用 Shi-Thomasi 角点。

为了可靠地恢复渐晕，重要的是在图像上均匀采集特征，以覆盖整个径向范围。因此，工程上将图片划分为若干个网格单元，并从所有单元中采集总和为 N 个特征。这对于覆盖整个图像强度范围也是有益的，可以较好的约束响应函数。如果由于遮挡或场景点移出图像而丢失了特征，则从当前包含较少特征的单元中提取新特征。其中，使用长特征轨迹来增加径向运动，这对于渐晕估计是必要的，因为如果跟踪特征的径向运动很小，则不会捕获由于空间光度衰减引起的辐照度变化。

由于无法在较长时间内可靠跟踪的场景点（如地梯度区域）会严重干扰估计结果，因此采用前后向跟踪³，并对齐误差进行评估，以尽早滤除跟踪不良的对应关系。为了在不需要从图像中提取进一步特征的情况下增加测量次数，被 跟踪特征位置周围的小图像块中的所有像素都被包含在优化中。这样做有益的另一个原因是，为了可靠地跟踪，被跟踪的特征通常会位于较大的图像梯度上。因此，已经很小的几何跟踪误差将导致对应的图像亮度有很大的差异。提取图像块的目的是获得低梯度对应，相对于小的跟踪误差，其图像强度轮廓将不那么敏感 。

3. 优化后端

给定一组在一系列图像上跟踪的场景点 $P$ ，其中点 $p \in P$ 在帧 $F_p$ 中可见，根据式 $\eqref{1.2}$ 定义一个能量函数如下： $$ E = \sum_{p \in P} \sum_{i \in F_p} w_i^p \bigg\lVert \underbrace{O_i^p - f \big( e_i V(x_i^p) L^p \big)}_{r(f, V, e_i, L^p)} \bigg\rVert_h \tag{3.1}\label{3.1} $$ 其中，$O_i^p$ 是图像 $i$ 中点 $p$ 的输出强度，$e_i$ 是图像 $i$ 的曝光时间，$L^p$ 是点 $p$ 的辐照度，$x_i^p$ 是点 $p$ 在图像 $i$ 上的投影位置。$w_i^p$ 是为每一个残差 $r$ 定义的权重因子。代价函数使用 Hube 范数 $\lVert\cdot\rVert_h$ 作为鲁棒估计。需要注意的是，该能量公式是假定每个场景点都位于朗伯曲面的基础上。

对于 CRF 的建模，作者参照了 Grossberg 和 Nayar 引入的响应经验模型 (EMoR, empiric model of response)⁴ 。应用主成分分析 (PCA, principle component analysis) 来寻找通过选择参数 $c_k \in {\mathbb R}$ 线性组合平均响应 $f_0(x)$ 和基函数 $h_k(x)$ 形成的整体响应函数 $f_G (x)$ ， $$ f_G(x) = f_0 (x) + \sum_{k=1}^n c_k h_k(x) \tag{3.2} \label{3.2} $$ 其中，$c_k$ 为需要标定的参数，且有证明指出当 $n = 4$ 的时候就已经能够很好得表示响应经验模型。之所以采用该模型是由于对所有可能的参数化都表现出 CRF 的理想属性，例如 $f_G(0) = 0, f_G(1) = 255$ 。此外，它的导数可以很容易地通过简单地推导均值项和基函数来获得，这对于在非线性优化中需要推导雅可比矩阵提供了便捷。至于平均响应 $f_0(x)$ 和应用于 Database of Response (DoRF) 的 PCA 的前 25 个主要成分基函数 $h_k(x)$ 可以在 Camera Response Functions: Database (DoRF) and Model (EMoR) 中获取。

由于在没有大量对应关系的情况下，估计图像的每个像素位置的渐晕因子是不可实现的，因此采用了灵活的径向渐晕模型，假设衰减因子围绕图像中心对称，且渐晕中心位于图像中心。将之建模为一个六阶多项式， $$ V(x) = 1 + v_1 R(x)^2 + v_2 R(x)^4 + v_3 R(x)^6 \tag{3.3}\label{3.3} $$ 其中 $R(x)$ 是图像点 $x$ 相对于图像中心的归一化半径。

根据代价函数式 $\eqref{3.1}$ 的定义和各个优化对象的建模，采用 LM 法进行非线性优化。依据 2. 跟踪前端 方式会产生大量要估计的股照度的跟踪点，如果一次性对所有参数进行联合优化，那么密集型求解需要耗费大量的计算量。因此，利用优化问题的依赖结构将辐照度估计与其他参数解耦。

在第一步中，响应和渐晕函数的参数以及曝光时间通过假设相应场景点 $L^p$ 的辐射度为常数并为每个残差 $r$ 的相应行计算雅可比来更新 $$ {\boldsymbol J} = \left( \frac{\partial r}{\partial {\boldsymbol c}}, \frac{\partial r}{\partial {\boldsymbol v}}, \frac{\partial r}{\partial e_i} \right) \tag{3.4}\label{3.4} $$ 其中，${\boldsymbol c} = (c_1, c_2, c_3, c_4), {\boldsymbol v} = (v_1, v_2, v_3)$ 。设 $\boldsymbol e$ 为所有曝光时间的向量。然后可以通过求解下式方程来找到参数 $\Delta {\boldsymbol x} = (\Delta {\boldsymbol c}, \Delta {\boldsymbol v}, \Delta {\boldsymbol e})$ 的状态更新 $$ (\boldsymbol{J^T W J} + \lambda \ diag(\boldsymbol{J^T W J})) \Delta \boldsymbol x = - \boldsymbol{J^T W r} \tag{3.5} \label{3.5} $$ 其中 $\boldsymbol J$ 为完整的雅克比矩阵，$diag(\boldsymbol A)$ 表示提取输入矩阵 $\boldsymbol A$ 的对角线部分的操作，$\boldsymbol r$ 是残差向量，$\lambda \in {\Bbb R}$ 是 LM 优化的阻尼因子。

对角权重矩阵 $\boldsymbol W$ 是通过组合两个加权因子构建的，一个用于鲁棒 Huber 估计 $w^{(1)}_r$ ，第二个 $w^{(2)}_r$ 被选择用于降低高梯度图像位置处的残差，因为对于这些点，即使较小匹配对应估计的不准确会导致图像强度的较大误差。我们将残差 $r$ 的梯度相关权重 $w^{(2)}_r$ 定义为 $$ w^{(2)}_r = \frac{\mu}{\mu + \lVert \nabla F_i(x_i^p) \rVert_2^2} \tag{3.6}\label{3.6} $$ 其中 $\mu \in {\Bbb R}^+$ 是一个正常数，$\lVert \nabla F_i(x_i^p) \rVert_2^2$ 是图像 $F_i$ 中位置 $x^p_i$ 处的图像梯度的平方 L2 范数。这通常会降低跟踪图像块中心的残差的权重，同时对跟踪特征点附近的残差给予更高的重要性。然后通过将两个权重 $w^{(1)}_r$ 和 $w^{(2)}_r$ 相乘来给出残差的最终权重值。

第二步骤是更新场景点的辐照度。这个步骤可以高效地完成，因为场景点的辐射度独立于其他场景点的辐射度，并且所有其他参数在此优化轮次中都是固定的。首先，为每个 $p \in P$ 构造一个雅可比矩阵 $\boldsymbol J^p$ ，表示为其残差相对于场景点辐射度的偏导数 $$ \boldsymbol J^p = \left( \frac{\partial r}{\partial L^p} \right) \tag{3.7}\label{3.7} $$ 其次可以独立地为每个场景点计算辐射度更新 $$ \Delta L = \frac{-\boldsymbol J^T_p \boldsymbol W_p \boldsymbol r_p}{(1+\lambda) \boldsymbol J^T_p \boldsymbol W_p \boldsymbol J_p} \tag{3.8}\label{3.8} $$ 其中 $\boldsymbol W_p$ 为优化权重，$\boldsymbol r_p$ 是残差向量，$\lambda \in {\Bbb R}$ 是 LM 优化的阻尼因子。

然后，该算法执行多轮优化，在第一步中的响应、晕影和曝光时间优化和第二步中的辐射度优化之间交替进行迭代。由于保证每一轮都保证相对于能量执行一个下坡步骤，该方案最终将收敛到局部最小值。

3.1 离线标定

在离线模式下，可以联合优化所有光度参数，首先跟踪整个输入序列以获得场景点对应关系，然后安装上述优化式 $\eqref{3.1}$ 。对于大的序列，为了加快估计过程，可以将输入分割为恒定大小的优化块，并对每个块独立优化。但由于曝光时间的尺度未知，因此需要让这些块重叠一定数量的帧，并在这些重叠区域内使用最小二乘来对齐曝光。在算法第一次收敛后，通过删除产生最大误差的固定百分比残差来执行删除异常值。然后再次运行算法，以更好地拟合剩余的点。

3.2 在线标定校准

对于在线校准过程，必须尽快提供图像的光度校正。因此，首先收集大量图像以联合优化所有参数是不可行的。然而，为了可靠地估计渐晕和响应函数，需要多帧进行校准。由于可以逐帧估计曝光时间，因此将它们的估计与其他参数分离，立即为传入帧提供曝光时间估计。工程系统中保持当前晕影和响应估计的状态，随着更多帧的到达而连续更新，优化等式 $\eqref{3.1}$ 。在新帧到达时，通过根据当前估计移除响应和晕影来纠正它。然后，我们使用加权线性最小二乘误差能量公式联合计算最后 $M$ 帧中每一帧的曝光时间，该公式重新排列方程式 $\eqref{3.1}$ 的残差项，从输出强度中去除响应和晕影 $$ E = \sum_{i = 1}^M \sum_{p \in P} w_i^p \bigg( \underbrace{ \frac{f^{-1}(O_i^p)}{V(x_i^p)} - e_i L^p}_{r(e_i, L^p)} \bigg) \tag{3.9} \label{3.9} $$ 其中 $P_i$ 表示在第 $i$ 个图像中可见的场景点集，$f^{-1}$ 是响应函数的逆函数。每个残差现在仅取决于其帧的曝光时间和其场景点的辐射度。当固定跟踪点的辐射度时，等式 $\eqref{3.9}$ 成为一个可以有效求解的线性优化问题。我们用跟踪点的平均输出强度初始化辐射。

由于传入的帧会立即根据当前响应和渐晕估计进行校正，因此对所有光度参数进行相当慢的联合优化不再构成性能瓶颈，因为它可以在后台独立执行。由于 KLT 跟踪和曝光优化可以非常快速地执行，所提出的算法可以进行实时处理。下图显示了在在线校准模式下运行的已实现系统的算法概览。

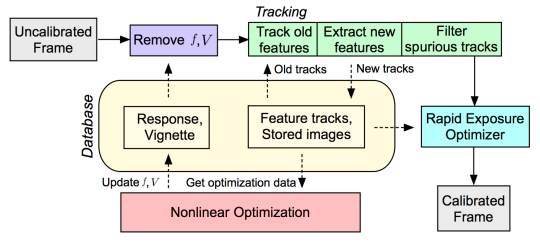
该系统保留一个数据库，存储晕影和响应函数估计以及跟踪的特征位置以及它们在输入图像中的输出强度。通过首先消除它们的响应和渐晕干扰来对新进入的帧进行光度校正。然后向前跟踪当前活动的特征，必要时提取新特征并过滤掉虚假轨迹。最后，估计帧的曝光时间并输出经过光度校准的帧。在后台，非线性优化基于收集的跟踪数据不断更新数据库的渐晕和响应估计。

4. 总结

作者在原文中对多组数据进行了实验证明，证明了该标定方式是可行有效且能得到一个令人满意的结果。并且实验证明该算法能够显著提高视觉里程计中直接法的质量。作者将算法开源在 tum-vision/online_photometric_calibration 上，并且给出了一个实验视频如下

Reference