Online Temporal Calibration in VINS

1. 数据同步

不同传感器之间的数据同步对融合算法至关重要，在 VIO 中，相机与 IMU 之间的数据同步对 VIO 精度影响非常大。那么如何评判一个系统数据同步的好坏呢？参照¹提供的图片来简单分析下。

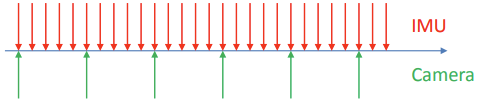
• 最优：传感器通过硬件触发的时间对齐

  

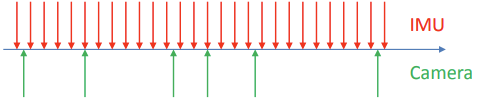
• 一般：传感器具有相同的时钟（例如，在相同的系统时钟上运行或具有全局时钟校正），但在不同的时间捕获数据

  

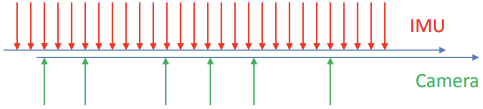
• 不好：传感器有不同的时钟（例如，每个传感器都有自己的振荡器）

  

由此引入一个名词：时间戳，即标记每一个传感器测量的时间。那么时间戳的好坏评价如下。

• 最优：时间戳在数据捕获时完成获取
• 一般：时间戳有固定延迟
  • 例如，时间经过一些固定时长的数据处理后标记在底层硬件上，不受任何动态 OS 调度任务的影响
• 不好：时间戳有可变延迟
  • 例如，根据 PC 时间将两个传感器插入 USB 端口和时间戳。时间戳受传感器到 PC 的数据传输延迟的影响

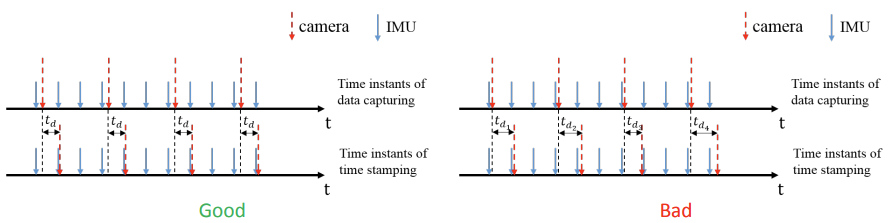
上述中，不好的数据时间同步将会对系统产生致命的影响，通常在硬件设计上要极力避免这种情况。而由于数据采集传输往往是需要一定时间的，因此要求硬件急速响应达到最优情况也比较难，亦或是成本过高。因此我们考虑在一般情况下，通过估计优化算法来标定不同数据之间的固定时间差。

2. 时间偏移

如下图所示，假设相机与 IMU 恰巧某一帧在同一时刻（设为 $t_0$）采样，由于曝光、 ADC 转码、数据传输等需要时间，相机数据在 $t_b$ 时间后才收到，而 IMU 数据在 $t_a$ 时间后才收到。一般在收到传感器数据后才打上时间戳，所以相机和 IMU 数据的时间戳分别为 $t_{cam} = t_0+t_b;,;t_{imu}=t_0+t_a$ ，由于 $t_a$ 与 $t_b$ 的不一致，使得本来在同一时刻采集的相机和 IMU 数据被打上不同的时间戳，从而造成了数据不同步。由此定义时间偏移 $t_d = t_a - t_b$ ，由于我们只关心两者之间的相对时间，所以只需要在图像时间上加上 $t_d$ 来补偿图像与 IMU 之间的时间误差，IMU 时间戳保持不变即可。

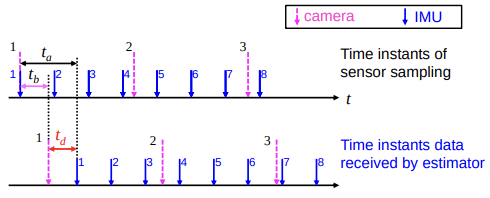
由此，我们定义时间偏移 $t_d$ 表示时间戳需要偏移的时间，以使得相机和IMU数据流对齐。 $$ t_{imu} = t_{cam} + t_d \tag{2.1} $$

注意： 式 (2.1) 中的 $t_d$ 为 IMU 的时延减去 Cam 的时延，为时钟对齐。

3. 时间偏移估计（方式一）

VINS-Mono/Fusion 中时间偏移估计的方式²¹³假设了特征点在短时间内以恒定速度在图像平面上移动，将 IMU 和相机的时间延迟，转换为在图像平面上的特征位置的延迟，以此简化整个误差函数。并且在每次优化后，补偿后续视觉流的时间戳，再次优化新的 $\delta t_d$ ，直至收敛到 $0$ 。

3.1 图像平面上的特征点速度

相对于移动整个相机或 IMU 序列，采用在时间线上移动特征的观察点。为此引入了特征速度，用于建模和补偿时间偏移。在很短的时间内（几毫秒），相机运动可以被视为匀速运动。因此，特征在短时间内在图像平面上以近似恒定速度移动。

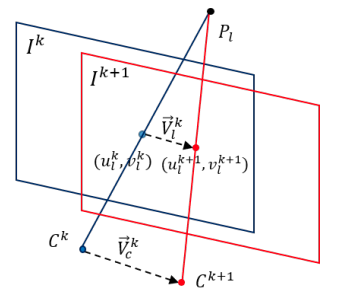
基于此假设，计算图像平面上的特征速度。对于上图，$I^k$ 和 $I^{k+1}$ 是两个连续图像帧，其中 $[u_l^k, v_l^k]$ 和 $[u_l^{k+1}, v_l^{k+1}]$ 分别是特征在图像平面 $I^k$ 和 $I^{k+1}$ 的 2D 观察点。假设相机在很短的时间内 $[t_k, t_{k+1}]$ 以匀速从 $C_k$ 移动到 $C_{k+1}$ 。当近似认为特征 $l$ 也在短时间内以匀速 $V_l^k$ 在图像平面上移动。则速度 $V_l^k$ 为： $$ V_l^k = \left( \begin{bmatrix} u_l^{k+1}\newline v_l^{k+1} \end{bmatrix} - \begin{bmatrix} u_l^k \newline v_l^k \end{bmatrix} \right) / (t_{k+1} - t_k) \tag{3.1} $$

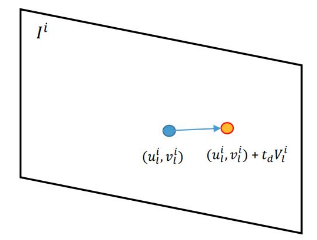
其中，带有时间偏移的 2D 特征位置表示为 $z_l^k(t_d) = [u_l^k \ \ \ v_l^k]^T + t_d V_l^k$ ，如下图所示。

3.2 带有时间偏移的视觉因子

在经典的稀疏视觉 SLAM 算法中，视觉测量的成本函数表示为（重）投影误差。我们通过添加一个新变量时间偏移来反映经典（重新）投影误差。一个特征有两种典型的参数化。一些算法将特征参数化为其在全局帧中的 3D 位置，而另一些算法将特征参数化为相对于某个图像帧的深度或逆深度⁴。下面，我们分别用这两种参数化将时间偏移建模为视觉因子。

3.2.1 全局 3D 位置参数

对于在全局坐标系下特征点的 3D 位置 $P_l = [x_l, y_l, z_l]^T$ 。传统方法中视觉测量被表示为重投影误差： $$ \begin{align*} e_l^k &= z_l^k - \pi({}^w_{c_k}R^T (P_l - {}^wp_{c_k})) \newline z_l^k &= [u_l^k \ \ \ v_l^k]^T \end{align*} \tag{3.2} $$ 其中 $z_l^k$ 为特征点 $l$ 在第 $k$ 帧的观测点，$({}^w_{c_k}R, {}^wp_{c_k})$ 为相机位姿，将特征点 $P_l$ 从全局坐标系转换到局部相机坐标系，$\pi(\cdot)$ 代表相机重投影模型，将 3D 特征点投影到畸变的相机平面中。

在上述公式中，摄像机姿态 $({}^w_{c_k}R, {}^wp_{c_k})$ 受视觉测量的约束。它也受到 IMU 测量的限制。在实际应用中，如果 IMU 与摄像机之间存在时间偏差，则 IMU 约束与视觉约束在时域上不一致。换句话说，我们应该向前或向后移动摄像机序列，使摄像机和 IMU 数据流在时间上保持一致。不过我们不是移动整个摄像机或 IMU 序列，而是在时间轴上移动特征观测。新的公式如下： $$ \begin{align*} e_l^k &= z_l^k(t_d) - \pi({}^w_{c_k}R^T (P_l - {}^wp_{c_k})) \newline z_l^k(t_d) &= [u_l^k \ \ \ v_l^k]^T + t_d V_l^k \end{align*} \tag{3.3} $$ 其中 $V_l^k$ 为特征点在图像平面上的速度，$t_d$ 为未知的时间偏移量。通过优化 $t_d$ ，可以找到时域中与 IMU 约束相匹配的最佳相机位姿和特征观察点。

3.2.2 局部深度参数

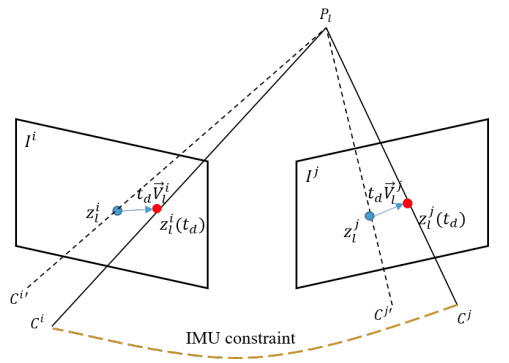
特征也可以被参数化为在图像坐标系下的深度或逆深度。以在图像 $i$ 中的深度 $\lambda_i$ 为例，传统方法从图像 $i$ 到图像 $j$ 的重投影误差为： $$ \begin{align*} e_l^j &= z_l^j - \pi({}^w_{c_j}R^T ({}^w_{c_i}R \lambda_i \begin{bmatrix} z_l^i \newline 1 \end{bmatrix} + {}^wp_{c_i} - {}^wp_{c_j})) \newline z_l^i &= [u_l^i \ \ \ v_l^i]^T, \quad z_l^j = [u_l^j \ \ \ v_l^j]^T \end{align*} \tag{3.4} $$ 其中 $l$ 首先被投影到全局坐标系下，然后再投影回局部坐标系 $j$ 下的图像平面中。而带有时间偏移 $t_d$ 的重投影误差为： $$ \begin{align*} e_l^j &= z_l^j(t_d) - \pi({}^w_{c_j}R^T ({}^w_{c_i}R \lambda_i \begin{bmatrix} z_l^i(t_d) \newline 1 \end{bmatrix} + {}^wp_{c_i} - {}^wp_{c_j})) \newline z_l^i(t_d) &= [u_l^i \ \ \ v_l^i]^T + t_d V_l^i, \quad z_l^j(t_d) = [u_l^j \ \ \ v_l^j]^T + t_d V_l^j \end{align*} \tag{3.5} $$ 下图描绘了重投影过程。 虚线表示没有时间偏移的传统重投影方法，实线表示考虑时间偏移的重投影，黄线表示 IMU 约束。 IMU 约束与传统的重投影约束不一致。 通过优化 $t_d$ ，我们可以在时域中找到与 IMU 约束匹配的最佳相机位姿和特征观察点。

3.3 带时间偏移的优化

通过使用上诉的视觉因子，可以轻松地将时间标定函数添加到基于视觉惯性紧耦合的非线性优化框架中，利用局部 BA 共同优化摄像机和 IMU 状态以及特征位置。

• VINS-Fusion 中 projectionTwoFrameOneCamFactor 实例，回顾⁴4 小节中介绍视觉因子，加上时间偏移有：

$$ \mathbf{r} _\mathcal{C}(\hat{z} _l^{c_j}, \mathcal{X}) = \pi_c({} _c^bR^T ({} _{b_j}^{w}R^T ({} _{b_i}^wR ({} _c^bR \frac{1}{\lambda_l} \pi_c^{-1}(\begin{bmatrix} {u} _l^{c_i} \newline {v} _l^{c_i} \end{bmatrix} - (t_d - t_d^i) V_l^{c_i}) + {}^bp_c) + {}^wp _{b_i} - {}^wp _{b_j}) -{}^bp_c) ) - (\begin{bmatrix} \hat{u} _l^{c_j} \newline \hat{v} _l^{c_j} \end{bmatrix} -(t_d - t_d^j) V_l^{c_j}) \tag{3.6} $$

对于式 (3.6) 中做下详细的描述，其中 $t_d^i$ 和 $t_d^i$ 是原先计算得到的补偿量，由此注意到 VINS-Mono/Fusion 中对时间偏移估计做了调整，通过移动后续视觉流的时间戳来补偿时间偏移， 然后系统估计后续补偿过的视觉测量和惯性测量之间的 $\delta t_d$ 。 $\delta t_d$ 将在后续数据流中迭代优化，最后将收敛到零。 随着时间间隔 $\delta t_d$ 的减小，基本假设（特征在短时间间隔内以恒定速度在图像平面上移动）越来越合理。 即使在开始时存在巨大的时间偏移（如数百毫秒），该过程也将逐渐地从粗略到精细地补偿它⁵。为了更好的说明为什么是负号，我们来捋顺下思路： IMU 积分到相机补偿时间 $t_{cam}’ = t_{cam}+t_d^* $ ，而图像特征点的在 IMU 时钟下真正采集时间点是 $\bar t _{cam}=t _{cam}+t_d$，因此我们需要移动特征点位置时间量为 $t _{cam}’ - \bar{t} _{cam} = t_d^* - t_d$ 。

• 对 $t_d$ 求雅克比

$$ \frac{\partial \mathbf{r}_\mathcal{C}}{\partial d_t} = - \begin{bmatrix} \frac{1}{C_z} & 0 & -\frac{C_x}{C_z^2} \newline 0 & \frac{1}{C_z} & -\frac{C_y}{C_z^2} \end{bmatrix} {} _c^bR^T {} _{b_j}^{w}R^T {} _{b_i}^wR {} _c^bR \frac{1}{\lambda_l} V_l^{c_i} + V_l^{c_j} \tag{3.7} $$

4. 时间偏移估计（方式二）

参照 MSCKF 中的方式⁶⁷，如果在 IMU 预积分中使用类似的方式（需要根据 IMU 预积分做些改动），那么对时间偏移的估计将不再是视觉因子为约束，而是在 IMU 因子中。思路与方法一相反，具体等实现并测试后添加(#TODO)。

Reference