动态环境下视觉里程计基于遮挡累积的移动物体检测

Moving object detection for visual odometry in a dynamic environment based on occlusion accumulation ¹

动态环境仍然是机器人技术的一个挑战。检测移动物体的能力可以将针对静态场景进行的各种研究结果扩展到动态环境。尽管已经进行了很多研究，如背景减除法来识别移动物体，但在运动物体占据图像大部分的场景（我们称之为“运动物体主导场景”）中效果不佳。 当移动物体在附近时，这种情况经常发生，应该作为重中之重来对待。

为了解决上述由动态环境引起的问题，我们提出了一种遮挡累积方法（Occlusion Accumulation Method）。所提出的方法利用从 VO 中获得的深度和相机姿态信息来检测没有特定背景模型的移动物体。一些使用稳健回归权重的直接 VO 方法在移动物体主导场景时，由于落入局部最小值而无法跟踪准确的摄像机姿势。论文作者使用截至前一个图像的估计摄像机姿势来区分移动物体，并将它们从图像中排除，以找到下一个摄像机姿势。如果只使用优化器中的鲁棒回归，当移动物体主导场景时，摄像机的姿势很可能是相对于移动物体估计的。在所提出的用稳健回归估计摄像机姿态的方法中，该方法在移动物体主导场景之前就排除了移动物体的影响。与每次处理图像时内存使用量都会增加的其他映射方法不同，无论图像序列的持续时间有多长，所提出的方法的内存需求并不大，因为它持续更新单一遮挡信息。

论文作者使用估计的相机姿势对之前的深度图像进行 warp 对齐（注意理解文章中的 warp 操作，代码中是一个 Inverse Warping），并与当前的深度图像相减。累积这些减去的值显示出与背景减去相似的结果，而不依赖背景建模。该方法对主导场景的移动物体的影响是稳健的，并避免了背景建模不正确时出现的其他问题。但偶尔有可能检测到一个原本静止的、被视为背景的移动物体。

移动物体分割

光照变化、移动物体、相机自运动等各种因素都会引起图像变化。 假设不违反照片一致性假设，在涉及到固定相机下的移动物体的静态场景中，图像变化表示移动物体。在一个有摄像机任意运动的动态场景中，我们可以通过用估计的摄像机姿态对以前的图像进行 warp 转换来获得一个无运动的图像。在获得无运动图像后，动态场景可以被视为静态场景。

1. 遮挡累积

当一个移动物体在场景中漫游时，深度会发生变化。深度变化可以分为两种。第一种是遮挡：物体会在运动方向的头部遮挡住背景。第二种是重现：背景将出现在运动方向的尾部。我们假设背景的深度比运动物体的深度大。经过静态背景后面的物体，如柱子、树等，不影响深度值。因此，我们认为深度值变小的像素是移动物体的像素。

遮挡映射图和 warp 转换函数分别定义为: $$ \begin{align*} \Delta Z_i (u, \xi_i^{i+1}) &= Z_i({\rm w}(u, \xi_i^{i+1})) - Z_{i+1}(u) \tag{1} \label{1} \newline {\rm w}(u, \xi_i^{i+1}) &= \pi \big(\exp(\xi_i^{i+1}) \pi^{-1}(u, Z_i(u)) \big) \tag{2} \label{2} \end{align*} $$ 其中，$Z_i(u)$ 表示第 $i$ 帧深度图，$u$ 是图像 $\Omega(w \times h)$ 中的像素，$\xi \in \mathbb{R}^6$ 表示表示第 $i$ 帧和第 $i+1$ 帧之间的 6-DOF 相机姿势参数。投影函数 $\pi: \mathbb{R}^3 \to \mathbb{R}^2$ 将一个三维点映射成一个二维图像像素。$\exp(\xi_i^{i+1}) \in \rm{SE}(3)$ 表示关联摄像机姿势参数 $\xi_i^{i+1}$ 的变换矩阵。

如果 $\Delta Z_i > 0$ 意味着深度变小，即发生了遮挡。否则， $\Delta Z_i < 0$​ 意味着深度增加，即重新出现。由此通过以下方式定义遮挡累积映射图： $$ \begin{align*} A_{i+1} (u) &= \Delta Z_i(u, \xi_i^{i+1}) + \tilde A_i ({\bf w}(u, \xi_i^{i+1})) \newline &\approx \Delta Z_i(u, \xi_i^{i+1}) + \sum_{k=1}^{i-1} \Delta Z_k({\bf w}(u, \xi_{k+1}^{i}), \xi_k^{k+1}) \newline &\approx Z_{k_u}({\rm w} (u, \xi_{k_u}^{i+1})) - Z_{i+1}(u) \end{align*} \tag{3} \label{3} $$ 对于 $\forall u \in \Omega$ ，初始遮挡累积映射图被设置为 $A_1(u) = 0$ ，$k_u$ 是首次观察到当前帧的像素 $u$ 的帧的索引。$\tilde A(u)$ 是 $A(u)$ 的截断， 在后面式 $\eqref{5}$ 和 $\eqref{6}$ 中描述。$k_u$ 处之前索引的 warp 变换后像素将不在观测窗口 $\Omega$ 内，因此无需计算。这些索引的 $\Delta Z$ 将设为零值。当 $A(u)$ 的截断步骤没有被触发时，由于 $A(u) = \tilde A(u)$，式 $\eqref{3}$ 中第二和第三行近似等式成立。可以将遮挡累积映射图解释为第 $k_u$ 帧与当前帧之间相减的结果。与背景减法不同的是，与背景减除相反，我们使用遮挡映射图 $\Delta Z_i(u, \xi_i^{i+1})$ 。 因此，该方法不需要依赖于背景识别或 3D 建图。

现有的深度传感器存在深度误差，其沿着深度值呈二次方增长。 为了处理这种测量不确定性，我们将阈值设置为： $$ \tau_\alpha (u) = \alpha \cdot Z(u)^2 \tag{4}\label{4} $$ 尽管我们将阈值设置为大于零，但不需要的误差值可以通过累积超过阈值。此外，负值也会被累积，这样遮挡就根本不可能超过阈值。为了减少它们的影响，我们将闭遮挡累积映射图 $A_i(u)$ 截断为 $\tilde A_i(u)$ ，具体步骤如下: $$ \begin{align*} \tilde A_i (u) &= 0 & {\rm for}\ \ & A_i (u) \leq \tau_\alpha (u) \tag{5} \label{5} \newline \tilde A_i (u) &= 0 & {\rm for}\ \ & \Delta Z_i (u, \xi_i^{i+1}) \leq -\tau_\beta (u) \tag{6} \label{6} \end{align*} $$ 式 $\eqref{5}$ 中的截断步骤可能会干扰对缓慢接近摄像机的运动物体的检测。然而，一旦检测到移动物体，$\Delta Z_i (u, \xi_i^{i+1})$ 的小值将被反映出来。当背景重新出现时，由于深度误差的积累， $A_i(u)$ 将不会低于阈值 $\tau_\alpha (u)$ 。式 $\eqref{6}$ 中的截断步骤有助于检测背景的重新出现。远离摄像机的移动物体几乎不会超过阈值。即便如此，如果超过了阈值，该物体很快就会在场景中消逝。遮挡累积的结果如下图所示。为了帮助理解，$A(u)$ 还没有通过每次迭代用式 $\eqref{5}$ 进行截断。由于没有物体附近测量的深度值，所以 图-d 中出现了类似条纹的结果。

遮挡累积法的说明：$A(u)$ 表示 $\Delta Z(u)$ 随时间的累积。亮区是指 $A(u)$ 显示为正值的区域，被认为是移动的物体，暗区是指 $A(u)$​ 显示为负值的区域，背景再次显现。中间的灰色代表一个零的值。由式 $\eqref{7}$ 得出的移动物体检测结果显示在 (b) 中。被认为是移动物体的区域被涂成紫色。

在计算 $A_i(u)$ 之后，我们截断遮挡累积映射图，以区分运动物体和背景。如果一个移动物体显示出适当的遮挡，背景图 $B_i(u)$ 将显示为 0 。否则，如果移动物体已经过去，背景再次出现， $B_i(u)$ 将显示 1 ，即： $$ B_i(u) = \begin{cases} 0 & {\rm if} \ A_i(u) > \tau_\alpha (u) \newline 1 & {\rm otherwise} \end{cases} \tag{7} \label{7} $$ 移动物体的掩码可以通过计算 $B_i(u)$ 的逆得到。

2. 深度补偿

通常情况下，深度图像在物体的边缘或图像窗口的边界附近有无效的深度。其效果如上图 (d) 所示。上图 (b) 中的分割在移动物体上方有空隙。当前帧中的一些无效深度值可以通过式 $\eqref{8}$ 来补偿，其中像素 $\bar u$ 上的未测量深度满足 $Z(\bar u) = 0$ ，补偿后的深度被用于下一张深度图像。 $$ Z_i(\bar u) = Z_{i-1} ({\rm w}(\bar u, \xi_i^{i-1})) \tag{8} \label{8} $$ 深度补偿的结果如下图所示。原始深度图像在物体边界附近有未测量的区域，颜色为黑色。如下图 (b) 所示，物体边界上的未测量区域用先前的深度图像填充。通过补偿后的深度图像，现在 $A(u)$ 可以被合理地计算出来（下图-c ）。因此物体分割可以覆盖整个运动物体（下图-d）。

3. 新探索区域的遮挡预测

假设有一个新探索的区域，它必须被分类为动态场景中的背景或移动物体。这个时候新探索区域的像素 $\tilde u$ 处的遮挡映射图 $\Delta Z_i(\tilde u, \xi_{i-1}^i)$ 不能正确被计算，因为 warp 转换前一帧像素 ${\bf w}(\tilde u, \xi_i^{i-1})$ 不在图像窗口 $\Omega$ 中。我们将新发现的区域定义为： $$ \bar \Omega = \lbrace \tilde u | {\rm w}(\tilde u, \xi_i^{i-1}) \notin \Omega \rbrace \tag{9} \label{9} $$ 文章中建议用快速行进法 (Fast Marching Method) 预测 $A(\tilde u)$ 的方法如下： $$ A_i(\tilde u) = \frac{\sum_{\delta u \notin \tilde \Omega} \lbrace A_i (\delta u) + \nabla_{\delta u} Z_i(\tilde u) \rbrace}{ \sum_{\delta u \notin \tilde \Omega} 1} \tag{10} \label{10} $$ 其中 $\delta u$ 表示 $\tilde u$ 的最近邻像素，其累积值 $A(\delta u)$ 已经被计算，$\nabla_{\delta u} Z_i(\tilde u) = Z_i(\tilde u) - Z_i(\delta u)$ 是深度图相对于 $\delta u$ 的梯度。因为 $A(u)$ 与深度图有对应关系，所以使用深度图的梯度和与已知区域相邻的最近像素 $\delta u$ 的遮挡积累映射图来预测 $A(\tilde u)$ 。换句话说，我们用 $A_i (\delta u) + \nabla_{\delta u} Z_i(\tilde u)$ 的平均值对 $A(\tilde u)$ 进行插值。之后，我们通过 $\tilde \Omega \gets \tilde \Omega - {\delta u}$ 更新新探索的区域，并重复式 $\eqref{10}$ 直到 $\tilde \Omega = \phi$ 。这个过程在两个连续的帧上操作。过程示例如下图所示。

由于新探索的区域的效果在两个连续的帧中是不明显的，我们在 下图-d 中与具有较长时间间隔的帧比较了被遮蔽的图像。

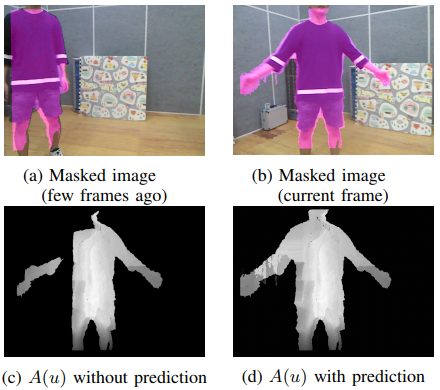
新探索区域的遮挡预测示例：当摄像机移动时检测到一个新的区域，在之前几帧没有深度信息。在这样的区域，遮挡映射图的值为零。(c) 显示了由于新探索的区域而产生的未测量的深度值的影响。在执行了遮挡预测方法后， $A(u)$ 在 (d) 所示的新探索的区域有适当的遮挡映射值，从 (d) 得到的移动物体检测结果显示在 (b) 。

在被认为是移动物体的预测 $A(u)$ 的正面区域，背景深度从未被检测到，因为在当前图像之前，背景一直被移动物体遮挡着。该算法可能无法识别以这种方式出现的背景。因为即使背景出现， $A(u)$ 也可能不低于式 $\eqref{7}$ 中的阈值。但之后会由于触发式 $\eqref{6}$ 的截断，使背景识别正常工作。预测的结果在上图中描述。当预测区域外没有最近的移动物体时，我们将预测区域的 $A(u)$ 删除以防止错误传播。另外，如果有小尺寸的移动物体标签，我们会将其抑制，因为它们通常可以忽略不计。

鲁棒的姿态估计

在论文中，作者使用 DVO² 结合移动物体检测进行相机位姿估计作为示例。系统框架图如下所示：

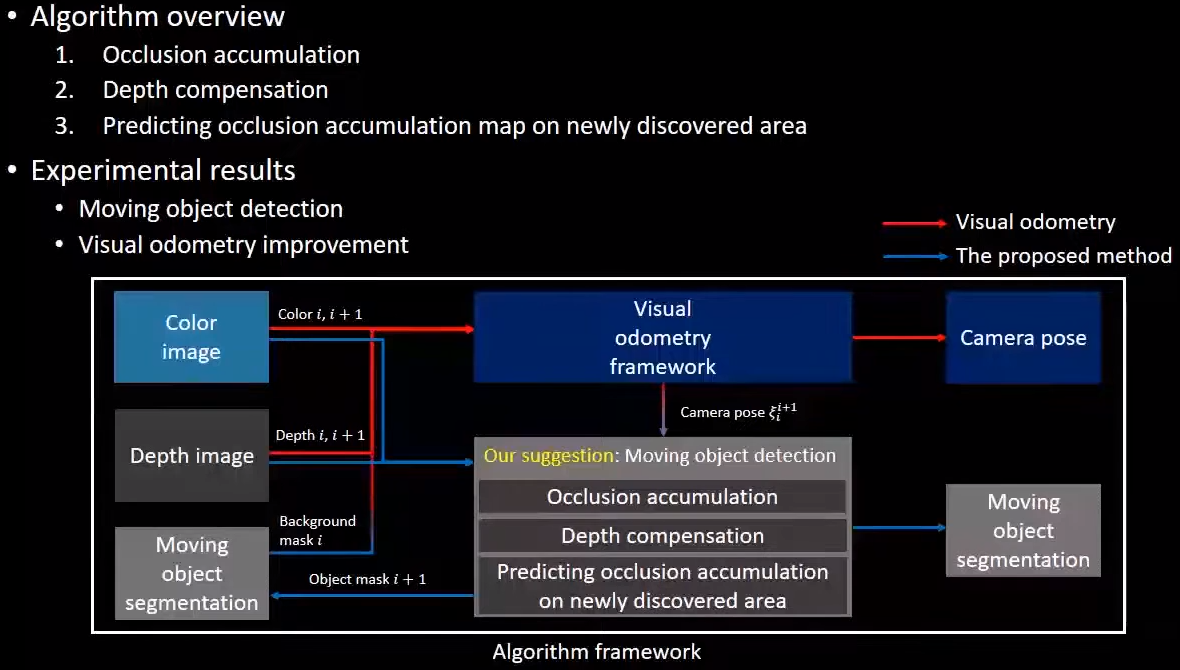
最初，只用 RGB-D 图像的序列来估计摄像机的运动。在检测到移动物体后，结合背景掩码 $B(u)$ 对摄像机的运动进行估计。仅使用鲁棒回归的方法可以有效地估计含义小范围内运动物体的自我运动，但当运动物体的区域很大时，它将达到局部最小解，因为背景与运动物体混淆了。反之，添加移动物体检测在排除了到当前帧为止检测到的运动物体后，剩余的运动物体区域足够小，可以估计获得更加准确的摄像机姿态。而且，由于相机姿态更加准确，上文提及的移动物体检测方法更加不会混淆背景和移动物体。相机的姿态估计是通过最小化成本函数实现的，如式 $\eqref{11}$ 所示。在成本函数中，使用了式 $\eqref{13}$ 中的双平方准则，使之完全忽略了离群值的影响。这一特性使我们可以通过最小化背景像素相应残差来获得摄像机的姿态 $\xi$ 。 $$ \begin{align*} \xi_i^{i+1} &= \underset \xi {\arg\min} \sum_{u \in \Omega} B_i( {\rm w}(u, \xi)) J_i(u, \xi) \tag{11} \label{11} \newline J_i(u, \xi) &= \rho_{k_I} (\Delta I_i(u, \xi)) + \gamma \cdot \rho_{k_Z} (\Delta Z_i(u, \xi)) \tag{12} \label{12} \newline \rho_k(e) &= \begin{cases} \frac{k^2}6 \Big( 1 - \big( 1 - (\frac{e}{k})^2 \big) \Big) & {\rm for} \ \ |e| \leq k \newline \frac{k^2}6 & {\rm for} \ \ |e| > k \newline \end{cases} \tag{13} \label{13} \end{align*} $$ 式 $\eqref{12}$ 中的符号 $I_i$ 是第 $i$ 帧彩色图像，$k$ 是用户定义的双平方阈值。大于 $k$ 的残差值 $\Delta I$ 和$\Delta Z$ 不影响优化过程。作者使用 LM 优化器，并使用参数值$k_I=48/255，k_Z=0.5，\gamma=0.001$。论文作者的项目介绍网站为：Occlusion-Accumulation 。个人 C++ 实现版本：LSXiang/OcclusionAccumulation 。

Reference