A Fast and Robust Novel Online Rectification Algorithm
双目立体算法通常假设一对校正的图像作为输入,而双目相机设备通常都有出厂标定。然而,双目原本的结构可能随着设备使用的过程中发生了微小的形变,使得深度立体算法的最初假设不成立,由此会严重影响性能。因此,双目在线自校正功能的需求越来越备受关注。文献 1 提出了一种快速稳健的新型在线校正算法,针对已知镜头内参与畸变系数的先前条件下获取双目相机的外参以便精准匹配恢复出深度信息。其基本思路是将这一校正问题建模为对两台相机中每一台相机的矫正旋转 $\omega_0, \omega_1$ 的估计,并保持基线固定。这是更为常见的以估计旋转 $R$ 和平移 $t$ 算法形式的变形方式。在这两种情况下,需要估计的参数都为 5 个,因此位移尺度是未知的。通常情况下往往假设 baseline $\lVert t \rVert$ 的长度是固定不变的。
根据上述的建模方式,可以得到一种更简单的对称方式,通过设定重新校正之前和之后保持世界坐标系 $x$ 轴与双目设备的基线对齐,并将基线长度定义为 $b = 1$ ,而仅仅计算两个相机的旋转校正。由此,将问题转变成通过恢复每台相机的偏航角 $(\omega_{y_0}, \omega_{y_1})$ 、滚转角 $(\omega_{z_0}, \omega_{z_1})$ ,和相对俯仰角 $\Delta \omega_x = \omega_{x_1} - \omega_{x_0}$ (因为绝对俯仰 (矫正平面围绕 $x$ 轴旋转的角度) 是一个自由参数)来进行双目立体校准。(注:对于提到的 yaw, roll, pitch 的描述是针对镜头朝向拟似飞机头所表述的)除了上式的 5 个相对姿态的外参之外,算法设计还估计了模型化相对尺度的第 6 个参数 $\Delta f$ ,即焦距的微小变化 $f_0 / f_1 = 1 + \Delta f$ 。在实践中,发现补偿相对尺度非常重要,因为焦距随温度而变化。
基于上述模型的假设,我们重新对双目投影模型进行推导。设一个 3D 点 $P = (X,Y,Z)$ 在双目相机中分别被投影到坐标 $(u_0, v_0)$ 和 $(u_1, v_1)$ 上,假设已经进行畸变校准且已知对应的相机内参(焦距 $f_i$ 和光心 $c_{x_i}, c_{y_i}$ ),将其转换为归一化图像坐标为 $x_i = (u_i - c_{x_i}) / f_i$ ,$y_i = (v_i - c_{y_i}) / f_i$ 。根据模型假设,两个相机分别位于坐标 ${\bf t}_0 = [0\ 0\ 0]^T$ 和 ${\bf t}_1 = [1\ 0\ 0]^T$ 处,其它们的旋转分别为 $R_0 = R(-\omega_0)$ 和 $R_1 = R(-\omega_1)$ (注:由于 $R_i$ 表示为将空间点从 rectification 坐标系旋转到 src 坐标系下,因此这里基于 rectification 坐标系的旋转 $\omega_i$ 转变成 $R_i$ 时候需要添加负号 “$-$” ) 。因为预计旋转修正很小所有对旋转采用线性近似:
$$ R(\omega) = I + \lfloor \omega \rfloor_\times = \begin{bmatrix} 1 & -\omega_z & \omega_y \newline \omega_z & 1 & -\omega_x \newline -\omega_y & \omega_x & 1 \end{bmatrix} \tag{1} \label{1} $$
由此,将点 $P$ 投影到左相机的归一化平面有: $$ \begin{bmatrix} x_0 \newline y_0 \newline 1 \end{bmatrix} \sim \begin{bmatrix} \newline I + \lfloor -\omega_0 \rfloor_\times \newline \ \end{bmatrix} \begin{bmatrix} X \newline Y \newline Z \end{bmatrix} \sim \begin{bmatrix} \newline I - \lfloor \omega_0 \rfloor_\times \newline \ \end{bmatrix} \begin{bmatrix} X \newline Y \newline Z \end{bmatrix} \tag{2} \label{2} $$ 将逆深度(视差)参数化为 $d = 1/Z$ ,那么反投影为, $$ \begin{bmatrix} X \newline Y \newline Z \newline 1 \end{bmatrix} \sim \begin{bmatrix} X/Z \newline Y/Z \newline 1 \newline 1/Z \end{bmatrix} \sim \left[ \begin{array}{c|c} \newline I + \lfloor \omega_0 \rfloor_\times & {\bf 0} \newline \newline \hline {\bf 0} & 1\end{array} \right] \begin{bmatrix} x_0 \newline y_0 \newline 1 \newline d \end{bmatrix} \tag{3} \label{3} $$ 由此将之投影到右相机得为, $$ \begin{align*} \begin{bmatrix} x_1 \newline y_1 \newline 1 \end{bmatrix} &\sim \left[ \begin{array}{c|c} \newline I - \lfloor \omega_1 \rfloor_\times & {\bf 0} \newline \ \end{array} \right] \left[ \begin{array}{c|c} & 1 \newline I & 0 \newline &0 \newline \hline {\bf 0} & 1 \end{array} \right] \left[ \begin{array}{c|c} \newline I + \lfloor \omega_0 \rfloor_\times & {\bf 0} \newline \newline \hline {\bf 0} & 1\end{array} \right] \begin{bmatrix} x_0 \newline y_0 \newline 1 \newline d \end{bmatrix} \tag{4.a} \label{4.a} \newline &\approx \begin{bmatrix} \newline I - \lfloor \omega_1 - \omega_0 \rfloor_\times \newline \ \end{bmatrix} \begin{bmatrix} x_0 \newline y_0 \newline 1 \end{bmatrix} + \begin{bmatrix} \newline I - \lfloor \omega_1 \rfloor_\times \newline \ \end{bmatrix} \begin{bmatrix} d \newline 0 \newline 0 \end{bmatrix} \tag{4.b} \label{4.b} \newline &= \begin{bmatrix} \newline I - \lfloor \Delta \omega \rfloor_\times \newline \ \end{bmatrix} \begin{bmatrix} x_0 \newline y_0 \newline 1 \end{bmatrix} + d \begin{bmatrix} 1 \newline - \omega_{z_1} \newline \omega_{y_1} \end{bmatrix} \tag{4.c} \label{4.c} \end{align*} $$ 其中,$\Delta \omega = \omega_1 - \omega_0$ 是两个相机的相对旋转。根据上式可知对应 $d=0$ (即无穷原点),只能恢复相对的旋转 $\Delta \omega$ 。对于较近的点 $(d < 0)$ ,可以得到一个绝对的滚转和偏航,但无法得到绝对的俯仰。应证前面模型讨论。
如果使用 $\Delta x = x_1 − x_0$ 作为我们对 $d$ 的估计并且还引入尺度校正 $(1 + \Delta f)$,则有 $$ \begin{align*} \begin{bmatrix} x_1 \newline y_1 \newline 1 + \Delta f \end{bmatrix} &\sim \begin{bmatrix} 1 & \Delta\omega_z & -\Delta\omega_y \newline -\Delta\omega_z & 1 & \Delta\omega_x \newline \Delta\omega_y & -\Delta\omega_x & 1 \end{bmatrix} \begin{bmatrix} x_0 \newline y_0 \newline 1 \end{bmatrix} + \Delta x \begin{bmatrix} 1 \newline -\omega_{z_1} \newline \omega_{y_1} \end{bmatrix} \tag{5.a} \label{5.a} \newline &= \begin{bmatrix} x_0 + \Delta\omega_z y_0 - \Delta\omega_y + \Delta x \newline y_0 - \Delta\omega_z x_0 +\Delta\omega_x - w_{z_1} \Delta x \newline 1 + \Delta\omega_y x_0 - \Delta\omega_x y_0 + w_{y_1} \Delta x \end{bmatrix} \tag{5.b} \label{5.b} \end{align*} $$
根据 $\eqref{5.a} \eqref{5.b}$ 中利用 $\enclose{circle}3 \times y_1 - \enclose{circle}2$ 得(其中 $\enclose{circle}n$ 表示向量中第 $n$ 行,$\Delta y = y_1 - y_0$): $$ \begin{bmatrix} 1+y_0 y_1 & -x_0 y_1 & -x_0 & -\Delta x y_1 & -\Delta x & y_1 \end{bmatrix} \begin{bmatrix} \Delta\omega_x \newline \Delta\omega_y \newline \Delta\omega_z \newline \omega_{y_1} \newline \omega_{z_1} \newline \Delta f \end{bmatrix} = \Delta y \tag{6} \label{6} $$ 文献 1 中使用 Harris 角点作为候选特征,并使用具有左右一致性检查的分层子像素 ZSSD2 特征匹配器在图像之间匹配它们。 对于每个匹配的特征点都有一个 $\eqref{6}$ 方程,收集成一个超约束系统,并使用鲁棒的最小二乘法求解过度约束的系统,迭代降低内点阈值以提高对异常值的鲁棒性。此外,由于通过假定测量视差 $\Delta x$ 对真实视差 $d$ 的近似仅在正确的相对方向附近成立,因此我们首先仅求解 $\Delta\omega$ 和 $\Delta f$,其方程不依赖于 $d$: $$ \begin{bmatrix} 1+y_0 y_1 & -x_0 y_1 & -x_0 & y_1 \end{bmatrix} \begin{bmatrix} \Delta\omega_x \newline \Delta\omega_y \newline \Delta\omega_z \newline \Delta f \end{bmatrix} = \Delta y \tag{7} \label{7} $$ 在文献 1 作者的实践中,估计这四个参数是非常稳定的。一旦这四个参数完成估计,就可以求解剩余参数 $\omega_{y_1}$ 和 $\omega_{z_1}$ 中的一个或两个,以恢复两个相机的绝对偏航和滚转(因为 $\Delta \omega_y = \omega_{y_1} - \omega_{y_0}$ 和 $\Delta \omega_z = \omega_{z_1} - \omega_{z_0}$ )。然而,只有当观察到的特征点分布在足够的深度范围内时,才能可靠地估计这些绝对角度。 在实践中,发现如果简单地在左右相机之间平均分配估计的相对角度,通常可以使用 4 参数模型为低分辨率图像获得令人满意的校正结果。
要宣布在线校正成功,要求至少有 100 个匹配的特征点,并且在 $|\Delta y|\leq1.0$ 的情况下,至少有 60% 的匹配率。此外,还检查计算出的矫正角度是否保持在保守的范围内(绝对俯仰和滚动 $<5^\circ$,相对偏航 $|\Delta\omega_y|<22^\circ$)。如果这些标准中的任何一个没有得到满足,就需要重新进行标定。在文献 1 作者将该校正算法用原型机拍摄的 185 个具有挑战性的测试图像对的实验, 下标列出了采用 3 参数和 4 参数模型的成功率和异常率,并证明估计 $\Delta f$ 在实践中很重要。
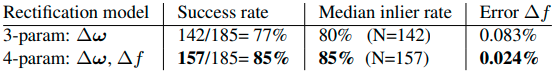
J. Wang, D. Scharstein, A. Bapat, K. Blackburn-Matzen, M. Yu, J. Lehman, S. Alsisan, Y. Wang, S. Tsai, J.-M. Frahm, Z. He, P. Vajda, M. Cohen, and M. Uyttendaele. A practical stereo depth system for smart glasses. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2023), Vancouver, Canada, June 2023. ↩︎ ↩︎ ↩︎ ↩︎
Suyog Patil, Joseph Simon Nadar, Jimit Gada, Siddhartha Motghare, Sujath S Nair. Comparison of Various Stereo Vision Cost Aggregation Methods . International Journal of Engineering and Innovative Technology (IJEIT) Volume 2, Issue 8, February 2013 ↩︎