High-Precision Online Markerless Stereo Extrinsic Calibration¹

立体相机和稠密立体视觉已经成为了机器人应用中最为广泛的传感方式之一。高精度的参数标定（包括各摄像机的内参 [intrinsic] 和立体外参 [extrinsic] ）是获得高质量、稠密深度测量的关键。一个好的立体标定使立体图像的转换成极线成为平行的。这是大多数密集立体匹配算法的基础，因为稠密立体匹配可以简化为在极线上的一维高效搜索问题。传统上，立体相机采用先进的材料和机械结构进行刚性安装，立体标定采用已知平面图案进行离线标定。然而，由于温度、振动或系统意外冲击的变化，标定参数往往会随着时间的推移而变化。因此，立体相机在线自校准的能力成为机器人使用基于立体的传感方式实现长期自主的关键因素。

1. 预备知识

首先从符号定义开始，观看下图–双目立体对极约束系统：

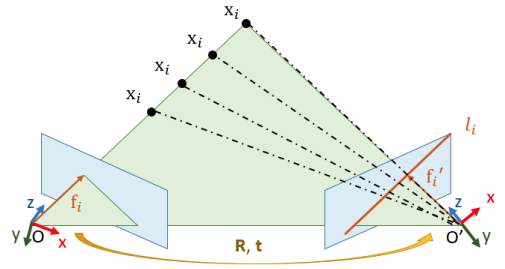
定义左右相机矩阵分别为 $K \in {\mathbb R}^{3\times3}$ 和 $K’ \in {\mathbb R}^{3\times3}$ ，假设 $K$ 和 $K’$ 是事先通过单目相机标定估计的已知量。假设在左右图像中都观测到一个特征 $i$ ，它位于左右相机光学中心坐标系的坐标分别 $x_i \in \mathbb{R}^3$ 和 $x_i’ \in \mathbb{R}^3$ ，且它投影到左右图像上坐标分别为 $(u_i, v_i)$ 和 $(u_i’, v_i’)$ 的像素上。而它对应与左右相机坐标系下的深度分别为 $\lambda_i$ 和 $\lambda_i’$ 。假设相机为针孔模型，那么 $x_i$ 和 $x_i’$ 对应的归一化像素坐标系为： $$ f_i = K^{-1} \begin{bmatrix} u_i \newline v_i \newline 1 \end{bmatrix}, \quad f_i’ = K’^{-1} \begin{bmatrix} u_i’ \newline v_i’ \newline 1 \end{bmatrix} \tag{1.1} \label{1.1} $$ 其中 $x_i = \lambda_i f_i$ ， $x_i’ = \lambda_i’ f_i’$ 。由于左右相机的坐标系可以通过一个旋转矩阵 $R \in {\mathbb R}^{3 \times 3}$ 和一个位移 $t \in \mathbb{R}^3$ 进行转换，因此有 $$ x_i’ = R \ x_i + t \tag{1.2} \label{1.2} $$ 一个本质矩阵 $E$（essential matrix）被定义为： $$ E = \lfloor t \rfloor_\times R \tag{1.3} \label{1.3} $$ 其中 $\lfloor \cdot \rfloor_\times$ 是反对称算子–将一个 $\mathbb{R}^3$ 向量转换成一个反对称矩阵。对于一个在左相机坐标系的三维空间中沿着 $f_i$ 方向的点，它投影到右相机平面的 $l_i$ 线上，其中线 $l_i$ 被称为极线。在数学上，极线 $l_i$ 可以携程本质矩阵 $E$ 和 $f_i$ 的乘积： $$ l_i = E \ f_i \tag{1.4} \label{1.4} $$ 而对极约束可以表示为： $$ (f_i’)^T \ l_i = (f_i’)^T \ E \ f_i = 0 \tag{1.5} \label{1.5} $$ 更为详细的对极几何知识可以参考²。

2. 算法模型化

由于检测到的特征点位置会受到来至于像素坐标量化与检测性能有限的噪声的影响，因此不能完全满足对极约束。每一对匹配特征 $f_i$ 和 $f_i’$ 的对极误差可以定义为： $$ \lVert (f_i’)^T \ E \ f_i \rVert^2 \tag{2.1} \label{2.1} $$ 它表示点 $f_i’$ 到极线 $l_i$ 在对极几何下的距离平方。我们的目标是求解一个 $R$ 和 $t$ 使得所有匹配的特征对应的整体极线误差最小： $$ \min_{R, t} \sum_{i=0}^N \lVert (f_i’)^T \lfloor t \rfloor_\times R \ f_i \rVert^2, \qquad s.t. \ \ \lVert t \rVert = 1 \tag{2.2} \label{2.2} $$ 单位范数约束 $\lVert t \rVert = 1$ 反应了一个事实，即，本质矩阵 $E$ 有 5 个自由度，3 个用于旋转 $R \in \rm{SO}(3)$ ，2 个用于任意尺度缩放的位移 $t \in \mathbb{S}^2$ （式 $\eqref{1.5}$ 满足任意比例因子与 $t$ 相乘）。 应用李群李代数原理，在当前旋转估计值 $\hat R$ 的正切平面空间参数化一个微小的扰动量 $\delta \theta \in \mathbb{R}^3$ ，有： $$ R \approx \hat R (I_3 + \lfloor \delta \theta \rfloor_\times) \tag{2.3} \label{2.3} $$ 其中， $I_3$ 表示为维度为 $3 \times 3$ 的单位矩阵。在当前位移估计值 $\hat t$ 的正切平面空间定义一个微小扰动量 $\delta t = [\alpha, \beta]^T$ ，可以参数化为： $$ t = \hat t + [b_1 \quad b_2] \delta t = \hat t + \alpha \ b_1 + \beta \ b_2 \tag{2.4} \label{2.4} $$ 其中，$b_1$ 和 $b_2$ 是切平面内的两个正交基向量，而 $\alpha$ 和 $\beta$ 是分别对应于以 $b_1$ 和 $b_2$ 为基向量的位移尺度因子。如下图所示，

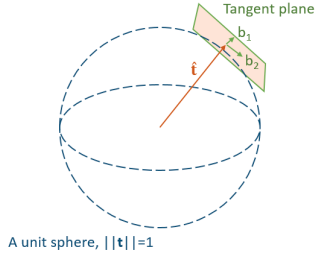
由于规定位移 $t$ 在 3D 空间可以任意尺度缩放，因此自由度只有 2 。如上图所示，将 $t$ 约束在一个单位球上，对于当前时刻估计值 $\hat t$ 的一个微小扰动可以定义在单位球的切平面上，则有 $t = \hat t + \alpha b_1 + \beta b_2$ 。其中，$b_1$ 和 $b_2$ 是切平面内的两个正交基向量，而 $\alpha$ 和 $\beta$ 是分别对应于以 $b_1$ 和 $b_2$ 为基向量的位移尺度因子

下面介绍基底 $b_1$ 和 $b_2$ 的求解方式。由于 $b_1$ 和 $b_2$ 约束在当前时刻估计值 $\hat t$ 的切平面上，因此它们都垂直于 $\hat t$ 。而且 $b_1$ 和 $b_2$ 并不是唯一的，可以是任意可以张成切平面的正交基底对。一种方式求解 $b_1$ 和 $b_2$ 的方式是使得 $b_1$ 、$b_2$ 和 $\hat t$ 互相正交。可以通过任意选取两个基地 $b_1$ 和 $b_2$ ，然后使用 Gram-Schmidt 过程逐个去除相关分量，直到满足正交约束。下面给出该算法过程的伪代码：

Algorithm 1 Projection( u, v )
$\quad$ return u $\cdot$ InnerProduct( u, v ) / InnerProduct( u, u )

Algorithm 2 FindingBases( $\hat t$ )
$\quad$ idx = 0;
$\quad$ if Absolute( $\hat t(1)$ ) < Absolute( $\hat t(idx)$ ) then
$\qquad$ idx = 1;
$\quad$ end if
$\quad$ if Absolute( $\hat t(2)$ ) < Absolute( $\hat t(idx)$ ) then
$\qquad$ idx = 2;
$\quad$ end if

$\quad$ if idx = 0 then
$\quad$ $b_1 = \lbrace 0, 1, 0 \rbrace, \ b_2 = \lbrace 0, 0, 1 \rbrace$ ;
$\quad$ else if idx = 1 then
$\quad$ $b_1 = \lbrace 1, 0, 0 \rbrace, \ b_2 = \lbrace 0, 0, 1 \rbrace$ ;
$\quad$ else
$\quad$ $b_1 = \lbrace 1, 0, 0 \rbrace, \ b_2 = \lbrace 0, 1, 0 \rbrace$ ;
$\quad$ end if

$\quad$ $b_1 = b_1 - {\rm Projection}( \hat t, b_1)$ ;
$\quad$ Normalize( $b_1$ );
$\quad$ $b_2 = b_2 - {\rm Projection}(\hat t, b_2) - {\rm Projection}(b_1, b_2)$ ;
$\quad$ Normalize( $b_2$ );
$\quad$ return $b_1, b_2$

• 1~7 行检测 $\hat t$ 的主要维度分量
• 9~15 行根据 $\hat t$ 的主要维度分量选择两个预备基底
• 17~20 行是利用 Gram-Schmidt 过程消除预备基底的关联分量
• 算法 2 中需要的投影函数在算法 1 里详细介绍

3. 非线性优化

通常情况下，立体相机的外参的先验值可以通过硬件结构亦或是 5 点法算法获取。由此，利用先验信息作为初始值通过在流形 $SO(3) \times \mathbb{S}^2$ 上迭代非线性优化参数求解 $E$，$R$ 和 $t$ 。使用 2. 算法模型化 中提出的参数化去优化方程 $\eqref{1.5}$ 。为了更好的表示，定义残差 $r_i(t, R) = (f_i’)^T \lfloor t \rfloor_\times R f_i$ 。那么残差 $r_i(t, R)$ 在当前估计值 $\hat t, \hat R$ 处的一阶泰勒展开为： $$ r_i(t, R) = r_i(\hat t, \hat R) + J_i(\hat t, \hat R) \cdot \Delta \tag{3.1}\label{3.1} $$ 其中 $\Delta = \lbrace \delta\theta, \delta t \rbrace \in \mathbb{R}^5$ 为误差状态向量，$J_i(\hat t, \hat R)$ 是残差 $r_i(t, R)$ 在当前估计值 $\hat t, \hat R$ 处关联 $\Delta$ 雅克比。则有： $$ \begin{align*} J_i(\hat t, \hat R) &= \bigg[ \frac{\partial r_i(\hat t, \hat R)}{\partial \delta \theta} \quad \frac{\partial r_i(\hat t, \hat R)}{\partial \delta t} \bigg] \newline \frac{\partial r_i(\hat t, \hat R)}{\partial \delta \theta} &= -(f_i’)^T \lfloor \hat t \rfloor_\times \hat R \lfloor f_i \rfloor_\times \newline \frac{\partial r_i(\hat t, \hat R)}{\partial \delta t} &= \Big[ (f_i’)^T \lfloor b_1 \rfloor_\times \hat R f_i \quad \ (f_i’)^T \lfloor b_2 \rfloor_\times \hat R f_i \Big] \end{align*} \tag{3.2}\label{3.2} $$

• $\frac{\partial r_i(\hat t, \hat R)}{\partial \delta \theta}$ 项推导

$$ \begin{align*} \frac{\partial r_i(\hat t, \hat R)}{\partial \delta \theta} &= \lim_{\delta \theta \to 0} \frac{(f_i’)^T \lfloor \hat t \rfloor_\times \hat R (I + \lfloor \delta \theta \rfloor_\times) f_i - (f_i’)^T \lfloor \hat t \rfloor_\times \hat R f_i}{\delta \theta} \newline &= \lim_{\delta \theta \to 0} \frac{(f_i’)^T \lfloor \hat t \rfloor_\times \hat R \lfloor \delta \theta \rfloor_\times f_i}{\delta \theta} \newline &= \lim_{\delta \theta \to 0} \frac{- (f_i’)^T \lfloor \hat t \rfloor_\times \hat R \lfloor f_i \rfloor_\times \delta \theta}{\delta \theta} \newline &= - (f_i’)^T \lfloor \hat t \rfloor_\times \hat R \lfloor f_i \rfloor_\times \end{align*} \tag{3.2a}\label{3.2a} $$

• $\frac{\partial r_i(\hat t, \hat R)}{\partial \delta t}$ 项推导

$$ \begin{align*} \frac{\partial r_i(\hat t, \hat R)}{\partial \alpha} &= \lim_{\alpha \to 0} \frac{(f_i’)^T \lfloor \hat t + \alpha b_1 + \beta b_2 \rfloor_\times \hat R f_i - (f_i’)^T \lfloor \hat t + \beta b_2 \rfloor_\times \hat R f_i}{\alpha} \newline &= \lim_{\alpha \to 0} \frac{(f_i’)^T \lfloor b_1 \rfloor_\times \hat R f_i \alpha}{\alpha} \newline &= (f_i’)^T \lfloor b_1 \rfloor_\times \hat R f_i \newline \newline \text{同理}, \quad \frac{\partial r_i(\hat t, \hat R)}{\partial \beta} &= (f_i’)^T \lfloor b_2 \rfloor_\times \hat R f_i \end{align*} \tag{3.2b}\label{3.2b} $$

将式 $\eqref{3.1}$ 代入式 $\eqref{2.2}$ 有： $$ \min_\Delta \sum_{i=0}^{N-1} \Big\lVert r_i(\hat t, \hat R) + J_i(\hat t, \hat R) \cdot \Delta \Big\rVert^2 \tag{3.3} \label{3.3} $$ 对 $\Delta$ 求导，使其为 0，得到下面线性方程的解： $$ J^T J \Delta = - J^T r \tag{3.4} \label{3.4} $$ 其中，$J$ 为雅克比矩阵 $J_i(\hat t, \hat R)$ 堆叠形成的雅克比矩阵，$r$ 为残差 $r_i(t, R)$ 堆叠形成的残差向量。为了缓解由于特征检测和匹配不完善而产生的异常值的影响，使用 Huber 加权范数对较大残差 $r_i(t, R)$ 进行加权： $$ w_i^h = \begin{cases} 1, & \rm{if} \ \ \lVert r_i(\hat t, \hat R) \rVert \leq c_t \newline \frac{c_t}{\lVert r_i(\hat t, \hat R) \rVert} & {\rm otherwise} \end{cases} \tag{3.5} \label{3.5} $$ 其中 $c_t$ 是一个预定义的 Huber 范数阈值。而数据归一权重 $w_i^n$ （在 3.1 归一化对极约束 说明）也将被使用，由此 $w_i = w_i^n \cdot w_i^h$ 。式 $\eqref{3.4}$ 可以被修改成加权式： $$ J^T W J \Delta = -J^T W r \tag{3.6} \label{3.6} $$ 其中 $W$ 是由权重 $w_i$ 构成的一个对角矩阵，那么 $\Delta$ 的解为： $$ \Delta = - (J^T W J)^{-1} J^T W r \tag{3.7} \label{3.7} $$ 通过迭代式 $\eqref{3.7}$ 并更新下式，直到收敛。 $$ \begin{align*} \hat R &\leftarrow \hat R \cdot \exp(\delta \theta) \newline \hat t &\leftarrow \hat t + \alpha b_1 + \beta b_2 \end{align*} \tag{3.8} \label{3.8} $$

3.1 归一化对极约束

在采用迭代优化求解的时候，为了缓解异常值与尺度坐标的不一致，通常采用马氏距离。上文中提到了在优化对极约束时候将采用归一权重 $w_i^n$ 使得估计器更为鲁棒。下面将结合论文中提及的参考文献³（相关内容位于该文献的 2.3 小节）进行这部分的介绍。

对极约束（式 $\eqref{1.5}$ ）给出了图像点对必须满足的唯一必要条件（与深度无关）。因此求解式 $\eqref{2.2}$ 从最小化目标函数中获得的运动估计对于常用的图像匹配噪声模型在统计上或几何上不一定是最优的。由此对每个图像点对赋予权重将是需要讨论的问题。在之前的一些文献⁴中观察到，为了得到更少的偏差估计，对极约束需要适当的归一化。

在透视投影的情况下（假设是针孔模型，其他模型于此类似）。图像点对归一化像素坐标 $f_i$ 和 $f_i’$ 的坐标形式 $f = [x,y,1]^T \in \mathbb{R}^3$ 。设图像匹配点对的检测模型如下： $$ f_i = \hat f_i + \epsilon_i \ , \quad f_i’ = \hat f_i’ + \eta_i \tag{3.9} \label{3.9} $$ 其中 $\hat f_i$ 和 $\hat f_i’$ 是理想的归一化坐标值（无噪声量），$\epsilon_i = [\epsilon_{i_1}, \epsilon_{i_2}, 0]^T \in \mathbb{R}^3$ 和 $\eta_i = [\eta_{i_1}, \eta_{i_2}, 0]^T \in \mathbb{R}^3$ 为检测噪声，而 $\epsilon_{i_1}, \epsilon_{i_2}, \eta_{i_1}, \eta_{i_2}$ 设为相同但相互独立符合高斯分布 $N(0, \sigma_f^2)$ 的随机变量。将式 $\eqref{3.9}$ 代入式 $\eqref{1.5}$ 有： $$ \begin{align*} (f_i’)^T \lfloor t \rfloor_\times R \ f_i &= \underbrace{(\hat f_i’)^T \lfloor t \rfloor_\times R \ \hat f_i}_ {0} + \eta_i^T \lfloor t \rfloor_\times R \ \hat f_i + (\hat f_i’)^T \lfloor t \rfloor_\times R \ \epsilon_i + \eta_i^T \lfloor t \rfloor_\times R \ \epsilon_i \newline &= \eta_i^T \lfloor t \rfloor_\times R \ \hat f_i + (\hat f_i’)^T \lfloor t \rfloor_\times R \ \epsilon_i + \eta_i^T \lfloor t \rfloor_\times R \ \epsilon_i \newline &\approx \eta_i^T \lfloor t \rfloor_\times R \ \hat f_i + (\hat f_i’)^T \lfloor t \rfloor_\times R \ \epsilon_i \end{align*} \tag{3.10} \label{3.10} $$

由于图像坐标 $f_i$ 和 $f_i’$ 往往远大于 $\epsilon_i$ 和 $\eta_i$ ，因此去除最后一项微小量。由此可得 $(f_i’)^T \lfloor t \rfloor_\times R \ f_i$ 是近似高斯分布 $N \big(0, \sigma^2 (\Vert \lfloor e_3 \rfloor_\times \lfloor t \rfloor_\times R f_i \Vert^2 + \Vert (f_i’)^T \lfloor t \rfloor_\times R \lfloor e_3 \rfloor_\times^T \Vert^2) \big)$ 独立随机变量。其中 $e_3 = [0, 0, 1]^T \in \mathbb{R}^3$ 。如果我们假设立体相机外参 $(R, t)$ 的先验分布是均匀的，那么 $(R, t)$ 的最大后验（MAP）估计是下面目标函数的全局最小值： $$ (R, t)_ {\rm MAP} \approx \arg\min g(R, t) = \arg\min \sum_{i=0}^{N-1} \frac{\lVert (f_i’)^T \lfloor t \rfloor_\times R \ f_i \rVert^2}{\Vert \lfloor e_3 \rfloor_\times \lfloor t \rfloor_\times R f_i \Vert^2 + \Vert (f_i’)^T \lfloor t \rfloor_\times R \lfloor e_3 \rfloor_\times^T \Vert^2} \tag{3.11} \label{3.11} $$ 这里采用 $g(R, t)$ 表示与对极约束相关的统计归一化目标函数。该目标函数在其它文献中也被称为梯度标准或对极改善。注意，在无噪声的情况下， $g(R, t)$ 就像其非归一化目标函数式 $\eqref{2.2}$ 一样达到 0。渐渐的，MAP 估计接近无偏最小均方差估计（MMSE）。因此，一般来说，MAP 估计器给出的偏置估计比非归一化目标函数式 $\eqref{2.2}$ 给出的偏置估计要少。而式 $\eqref{3.11}$ 中之所以使用 $\approx$ 是因为我们在式 $\eqref{3.10}$ 中丢掉了微小项。

由此我们可以得到上文中提到的数据归一权重 $w_i^n$ 为（其中 $e_1 = [1, 0, 0]^T \in \mathbb{R}^3$ ， $e_2 = [0, 1, 0]^T \in \mathbb{R}^3$ ）： $$ \begin{align*} w_i^n &= \frac 1{\Vert \lfloor e_3 \rfloor_\times \lfloor t \rfloor_\times R f_i \Vert^2 + \Vert (f_i’)^T \lfloor t \rfloor_\times R \lfloor e_3 \rfloor_\times^T \Vert^2} \newline &= \frac 1{(e_1^T \lfloor t \rfloor_\times R f_i)^2 + (e_2^T \lfloor t \rfloor_\times R f_i)^2 + ((f_i’)^T \lfloor t \rfloor_\times R e_1)^2 + ((f_i’)^T \lfloor t \rfloor_\times R e_2)^2} \end{align*} \tag{3.12} \label{3.12} $$

4. 立体相机标定外参的协方差估计

该小节将用数学方法推导出 3. 非线性优化 估计外参的协方差。依据式 $\eqref{3.9}$ 中假设的模型，且由于 $R$ 和 $t$ 的协方差等于误差状态 $\Delta$ 的协方差，因此，对于优化最终迭代的估计量 $\hat t$ 和 $\hat R$ ，计算式 $\eqref{3.7}$ 等式两边的协方差，得： $$ \begin{align*} \Sigma_\Delta &= (J^T W J)^{-1} J^T W \Sigma_r ((J^T W J)^{-1} J^T W)^T \newline &\approx J^{-1} (J^T W)^{-1} J^T W \Sigma_r (J^{-1} (J^T W) J^T W)^T \newline &= J^{-1} \Sigma_r J^{-T} \newline &= (J^T \Sigma_r^{-1} J)^{-1} \end{align*} \tag{4.1} \label{4.1} $$ 其中 $\Sigma_\Delta$ 是 $\Delta$ 的协方差，$\Sigma_r$ 是 $r$ 的协方差，$J^{-1}$ 是 $J$ 的伪逆，$(J^T W)^{-1}$ 是 $J^T W$ 的伪逆。由于检测到的特征是独立，因此 $\Sigma_r$ 是一个对角矩阵： $$ \Sigma_r = \begin{bmatrix} \rm{cov} \big( r_0(\hat t, \hat R) \big) & \cdots & 0 \newline \vdots & \rm{cov} \big( r_i(\hat t, \hat R) \big) & \vdots \newline 0 & \cdots & \rm{cov} \big( r_{N-1}(\hat t, \hat R) \big) \end{bmatrix} \tag{4.2} \label{4.2} $$ 有 $\rm{cov} \big( r_i(\hat t, \hat R) \big) = [(f_i’)^T \hat E \Sigma_f \hat E^T f_i’ + f_i^T \hat E^T \Sigma_f \hat E f_i]$ ，$\hat E = \lfloor \hat t \rfloor_\times R$ 。其中忽略微小量协方差。如果需要快速计算，还可以进一步简化 $\Sigma_\Delta$ 的计算，通过假设所有的协方差 $\rm{cov} \big( r_i(\hat t, \hat R) \big)$ 都相同（定义为 $c_r$），那么 $\Sigma_\Delta$ 可以近似为： $$ \Sigma_\Delta’ \approx c_r(J^T J)^{-1} \approx c_r \cdot (J^T W J)^{-1} \tag{4.3} \label{4.3} $$ 由于 $J^T W J$ 是求解式 $\eqref{3.6}$ 中的附属品，因此使用上式计算 $\Sigma_\Delta’^{-1}$ 不需要而外求解。从概率论的观点来看，$\Sigma_\Delta$ 的最大特征值反应了计算估计的准确性。

5. 工程实现

上文中提出的非线性算法需要一个精心设计的系统流程来支持以获得高精度的标定参数，如下图所示

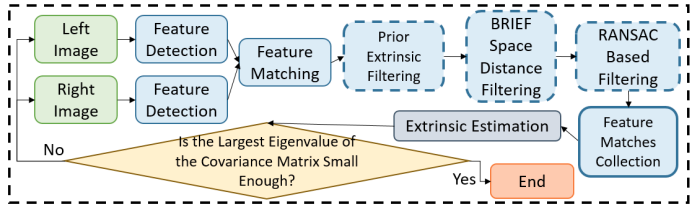
1. 对每一幅输入图像，采用 ST 角点检测器⁵检测图像上的特征点，并使用 BRIEF 关键点描述符⁶对其进行描述；
2. 根据 BRIEF 空间中的汉明距进行左右图特征点匹配；
3. 去除匹配异常值：
   • 利用来自立体相机外参的初始参数根据极线误差去除离群特征匹配点对；
   • 从左图到右图和从右图到左图的匹配需要检测一致性，且在 BRIEF 空间中，最佳匹配的汉明距需要小于第二佳匹配的三分之一。不满足这些唯一匹配检测的点对将去除；
   • 特征匹配需要具有相同的几何模型，如基础矩阵或本质矩阵，应用随机采用一致性进一步过滤异常值；
4. 特征点对收集时，为了满足实时性以及特征点尽量分布均匀。将图像分割成大小相等的 $W \times H$ 个单元，且每个单元中特征点数的上限设为 $c_m$ ，而特征点对将根据下面规则进行增加或删除：
   • 如果单元格未满，则保留并添加所有匹配的特征点；
   • 如果单元格已满，则仅保留特征视差差异最大的前 $c_m$ 个特征点对，其余的舍弃；
   • 如果单元格已满，且特征视差差异近似，那么随机保留 $c_m$ 个特征点对；
5. 根据上文提及的非线性优化算法进行对立体相机外参进行估计，且判断其协方差的最大特征值是否满足足够小，如果满足的话着标定结束，否则返回 1 。

代码实现：LSXiang/Stereo_Extrinsic_Self-Calibration

Reference