Marginalization-factor In VINS
1. VINS 的边缘化策略
VINS 的边缘化策略并不是一味地将新帧添加到滑窗内,移除老帧。为了处理一些静止(或小视差变化),VINS 做了些策略调整,具体如下:
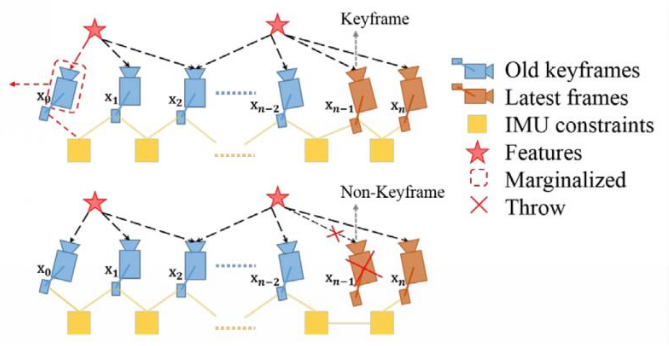
- MARGIN_OLD: 如果次新帧是关键帧,则丢弃滑动窗口内最老帧,同时对与该图像帧关联的约束项进行边缘化处理。丢弃 IMU 预积分;路标点保留,重新找个寄主。
- MARGIN_NEW: 如果次新帧不是关键帧,则丢弃当前帧的前一帧。因为判断当前帧不是关键帧的条件是当前帧与前一帧视差很小,这种情况下直接丢弃前一帧,去掉路标点与次新帧的共视关系,而两端 IMU 预积分拼接到一块,保证 IMU 预积分的连贯性。
利用这种策略可以针对于运动变化较小的情况,通过频繁的 MARGIN_NEW 保留那些比较老但是视差比较大的 Pose 。因为在运动变化较小的情况,如果一直 MARGIN_OLD 的话,那么视觉约束不够强,状态估计会受 IMU 积分误差影响,具有较大的累计误差。
2. 利用因子图1构建 Hessian 矩阵
当提及因子图,我们可能会立即想到 isam、isam2、gtsam1 这些庞然大物。不过下文并非使用因子图去求解最小二乘的优化问题以获取较高的效率,仅仅只是利用因子图的图形结构来说明如果快速的构建 Hessian 矩阵。
回顾 Bundle Adjustment 求解过程的三要素:误差项、优化变量、信息矩阵(或协方差),如下 $$ J^T \Sigma^{-1} J \delta x = - J^T \Sigma^{-1} e \tag{2.1} $$ 假设一个简单 VIO 的系统如下2:
视觉重投影约束:
- 误差项 = 估计值 - 观测值
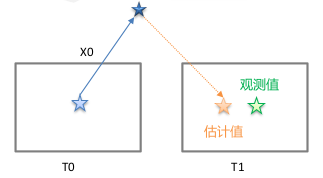
- 观测值:第 1 帧相机,观测到路标点 X0 的像素坐标,转化到归一化系中,为观测值;观测值是通过 LK 帧间跟踪得到
- 估计值:将路标点 X0 从第 0 帧,投影到第 1 帧的归一化相机系中,计算得到的坐标为估计值
- 优化变量:第 0 帧的位姿 T0、第 1 帧的位姿 T1、第 0 个路标点的逆深度 X0
- 协方差:像素误差 1.5 pixel
- 误差项 = 估计值 - 观测值
IMU 约束:
误差项 = 估计值 - 观测值
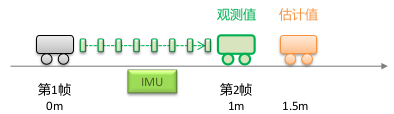
- 观测值: IMU 预积分得到的 PVQB 的变化量,为观测值
- 估计值:根据优化变量计算出来的两帧之间 PVQB 的变化量,为估计值
优化变量:第 1 帧和第 2 帧的位姿、速度、bias
协方差:IMU 预积分得到的协方差
| 约束 | 误差项 | 优化变量 | 协方差来源 |
|---|---|---|---|
| 视觉约束 | 重投影误差 [2x1] | 位姿、逆深度 | 像素观测误差(1.5 pixel) |
| IMU 约束 | PVQB 的运动误差 [15×1] | 位姿、速度、bias | IMU(acc、gyr)的噪声 |
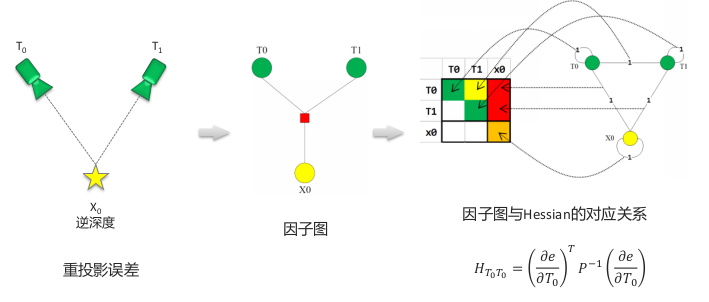
2.1 视觉约束因子图
方块为因子,圆圈为优化变量。一个因子为一个约束,即一个误差项,圆圈是与该误差项相关的优化变量。 构建 Hessian 矩阵块的方式是:将约束因子去掉,然后与该因子相连接的优化变量自身形成一条边,然后这些优化变量两两之间形成一个边,最后利用这些边求解。
2.2 IMU 约束因子图
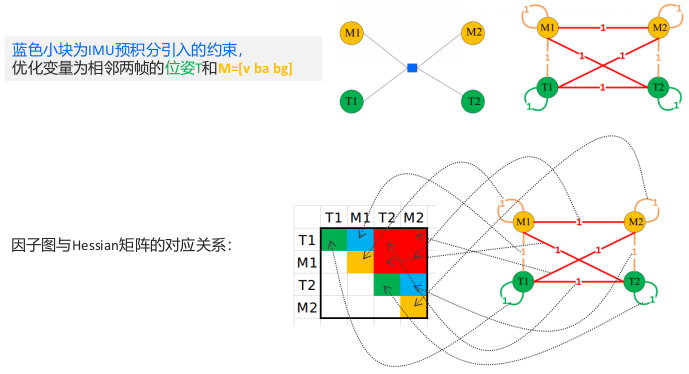
2.3 一个简单的 VIO 因子图
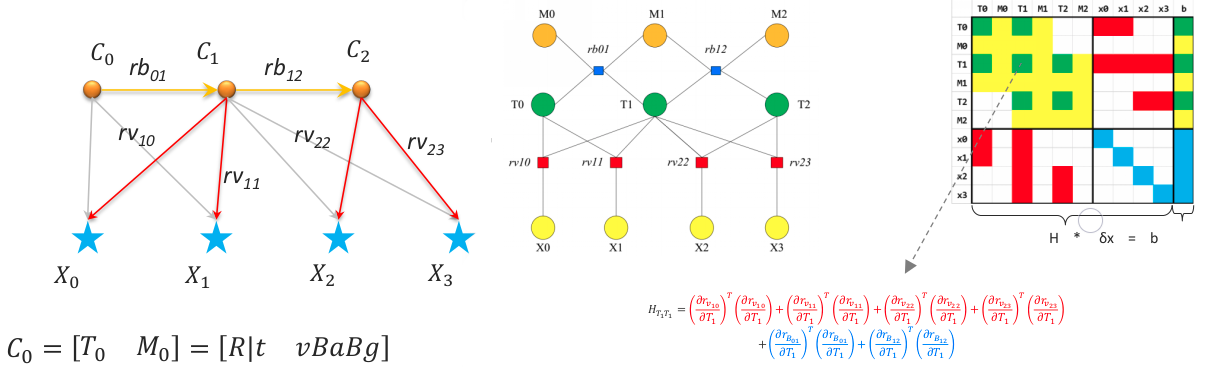
3. 利用因子图求解边缘化因子
我们先不管具体的代码流程,我们先从一个图化实例开始,一步步通过因子图来看如何构建一个边缘化因子。为了从易到难,首先假设系统第一次进行 Marginalizate,这个时候最初的边缘化因子为空,进行 Marginalizate 时仅由图像和 IMU 因子去构成边缘化因子。如下例子有:
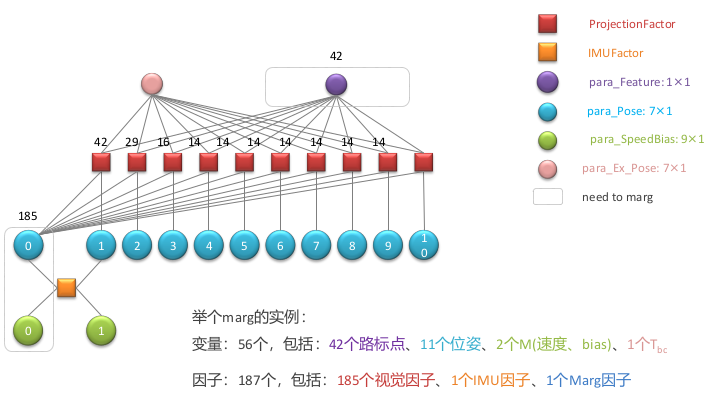
过程中需要用到 6 个关键变量(取至代码中的命名)
- parameter_block_size: 每个变量的维度
- parameter_block_data: 每个变量的数据
- parameter_block_idx: 每个变量在 H 矩阵中的索引,需要 marg 的变量放在前面
- pos: 所有变量的 local 维度总和,即 H 矩阵的维度
- m: 需要 marg 掉的变量的总维度
- n: 需要保留的变量的总维度
通过上图我们能知道所有变量的 local 维度总和,即 H 矩阵的维度: $$ \mathrm{pos} = {\color{YellowGreen}2(M_0,M_1)\times9} + {\color{Cyan}11(P)\times6} + {\color{Lavender}1(T_{bc})\times6} + {\color{RoyalPurple}42(\lambda)\times1} = 132 \tag{3.1} $$ 需要 marg 掉的变量的总维度: $$ m = {\color{YellowGreen}1(M_0)\times9} + {\color{Cyan}1(P_0)\times6} + {\color{RoyalPurple}42(\lambda)\times1} = 57 \tag{3.2} $$ 需要保留的变量的总维度: $$ n = \mathrm{pos} - m = 132 - 57 = 75, \quad 即: {\color{YellowGreen}1(M_1)\times9} + {\color{Cyan}10(P_0)\times6} + {\color{Lavender}1(T_{bc})\times6} = 75 \tag{3.2} $$ 由此我们可以构成如下列表:
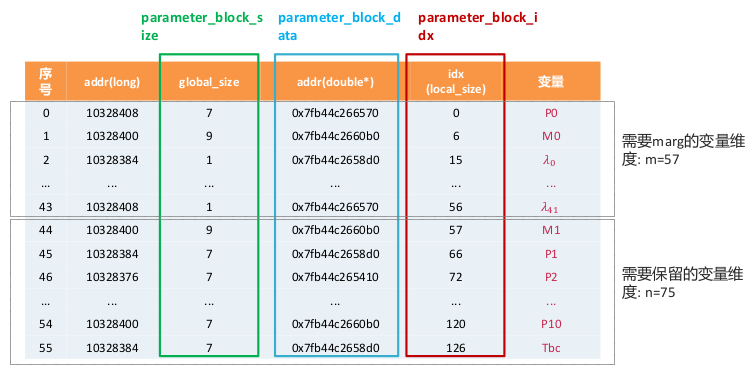
根据边缘化的知识,需要先构建一个边缘化的 Hessian 矩阵,然后利用舒尔补求解。对应上表的 Hessian 矩阵结构如下:
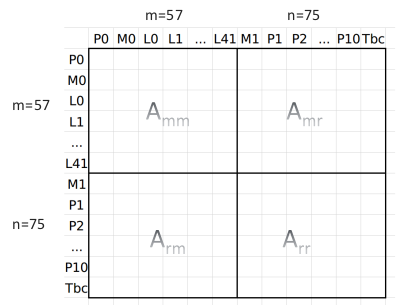
通过第 2 小节的因子图构建 Hessian 介绍,我们来对上图矩阵小块中填充对应的数值。首先一个视觉因子如下:
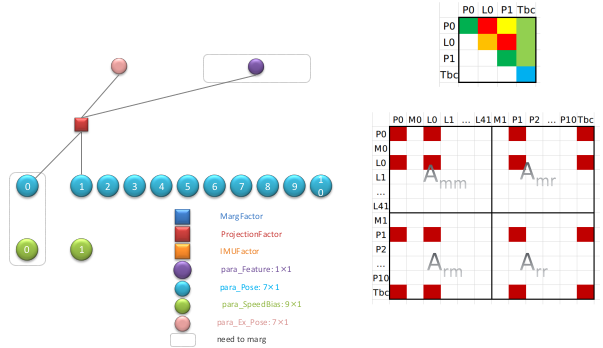
那么总共 185 个视觉因子填充到对于后得到结果如下:
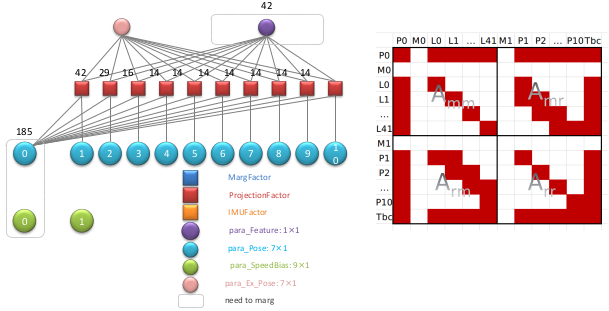
然后是一个 IMU 因子:
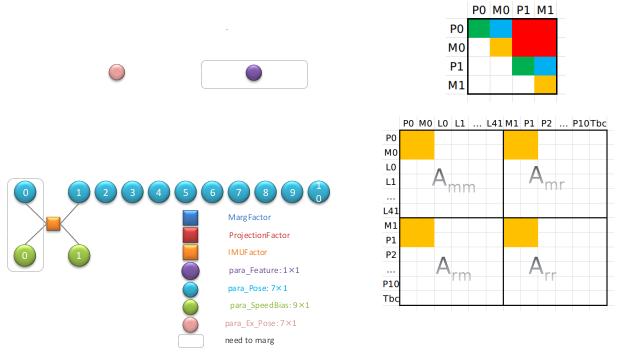
叠加 185 个视觉因子和一个 IMU 因子得到结果如下:
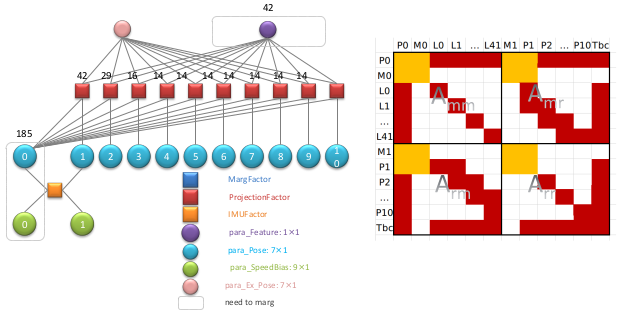
通过舒尔补进行 marginalization, 得到一个边缘化因子如下所示:
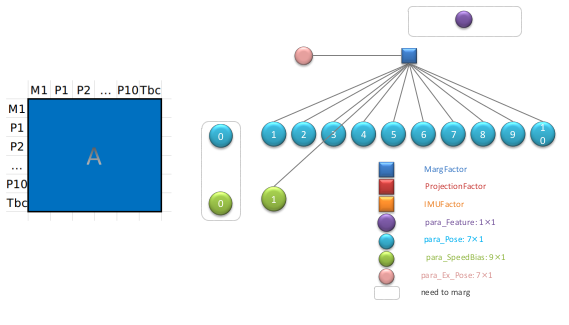
在最迟,我们假设了系统第一次进行边缘化处理,因此边缘化因子为空。那么如果在现在的基础上在进行一次滑动窗口的 marginalization 处理,在此之前的边缘化因子也需要参与到 marg 的过程中。那么这个时候的因子图结构如下所示:
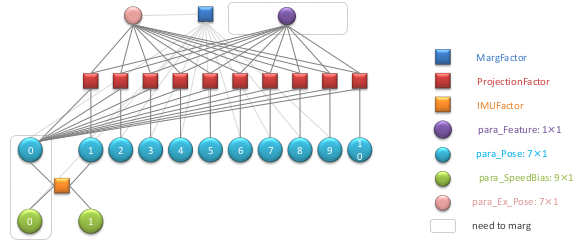
同样,利用因子图对 Hessian 矩阵中对应矩阵小块中填充对应的数值。一个边缘化因子对应如下:
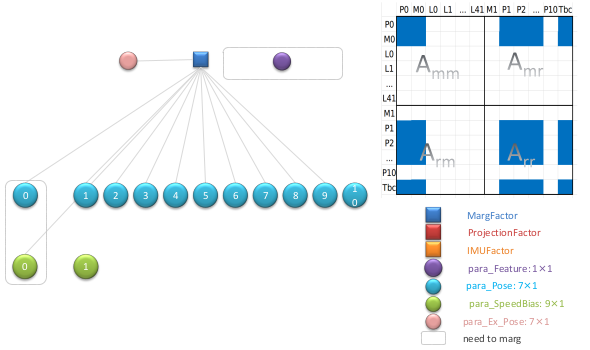
最终得到的 Hessian 矩阵如下:
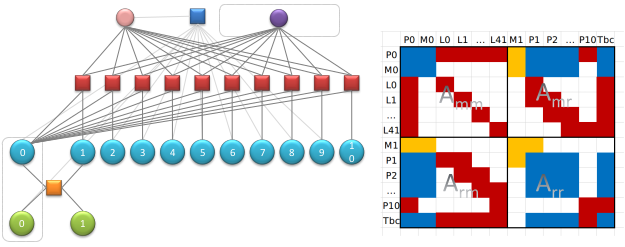
在此基础上再一次进行舒尔补计算,求解更新边缘化因子。之后就根据上面描述不断的计算求解迭代,一次次的更新得到新的边缘化因子。
4. 代码流程与解析
首先给出 VINS 中边缘化过程的代码流程图,如下
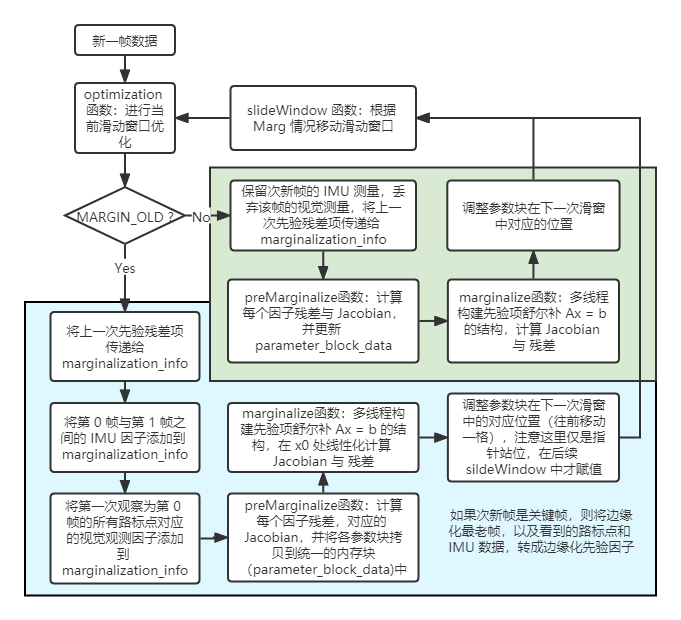
根据 Marginalization 知识3以及上文中相关的因子图流程,阅读代码应该已经不是什么太大的难题了。下面对代码中比较难理解(原先未提及的内容)作下解析。
4.1 由核函数引起的雅克比与残差缩放调整
我们知道在优化部分,视觉因子加了核函数,这样带来的问题就是其对应的残差与雅克比将发送变化。这个比较好理解,例如原先残差 $e(x)$ 的雅克比是 $J$ ,那么 $\rho(e(x))$ 的雅克比与值肯定发生了变化,其中 $\rho$ 是核函数。
这部分的原理参考4,其中用到了最小二乘的基本知识。让我们考虑一个如下问题: $$ \min_x \frac{1}{2} \rho(e^2(x)) \tag{4.1} $$ 那么有带鲁棒核函数的雅克比和 Hessian 矩阵如下: $$ \begin{align*} g(x) &= \rho’ J^T(x)e(x) \newline H(x) &= J^T(x) (\rho’ + 2 \rho’’ e(x) e^T(x)) J(x) \end{align*} \tag{4.2} $$ 其中省略 $e(x)$ 的二阶微分项。我们定义一个二阶近似如下: $$ \begin{align*} \rho(e^2(x+\delta x)) &\simeq \rho(e(x)) + g(x)\delta x + \frac{1}{2} \delta x^T H(x) \delta x \newline &\simeq \rho(e(x)) + \rho’ J^T(x)e(x)\delta x + \frac{1}{2} \delta x^T J^T(x) (\rho’ + 2 \rho’’ e(x) e^T(x)) J(x) \delta x \end{align*} \tag{4.3} $$ 利用最小二乘与高斯迭代的知识,求解式 (4.1) 可以转换成求解上式的最小值,因为二阶近似是个二次形,所以只要求解二次方程的顶点对应的 $\delta x$ 的即可。由此有:(令上式对 $\delta x$ 一阶导数等于 0) $$ J^T(x) (\rho’ + 2 \rho’’ e(x) e^T(x)) J(x) \delta x = -\rho’ J^T(x)e(x) \tag{4.5} $$ 由此我们可以以重新加权残差和雅可比矩阵,使得稳健的高斯-牛顿步骤对应于普通的线性最小二乘问题放入优化器中。其中有: $$ \begin{align*} \tilde{J}^T(x) \tilde{J}(x) &= J^T(x) (\rho’ + 2 \rho’’ e(x) e^T(x)) J(x) \newline -\tilde{J}^T(x) \tilde{e}(x) &= -\rho’ J^T(x)e(x) \end{align*} \tag{4.6} $$ 由此我们需要求得$\tilde{J}^T(x), \tilde{e}(x)$ (如果我们使用的不是 ceres-solver 而是 g2o 就不需要这么麻烦,而是直接添加到信息矩阵项中)。但在这个过程中我们需要注意的是式 (4.3) 中二阶近似的二阶项需要确保是正定的,即 $\rho’’ e(x) e^T(x) + \frac{1}{2} \rho’>0$ ,不然就没有解,由此我们需要调整如下。接下来这两个步骤我不太理解。
让 $\alpha$ 是下式的根, $$ \frac{1}{2} \alpha^2 - \alpha - \frac{\rho’’}{\rho’}\lVert e(x) \rVert^2 = 0 \tag{4.7} $$ 那么,重新加权残差和雅可比矩阵如下: $$ \begin{align*} \tilde{e}(x) &= \frac{\sqrt{\rho’}}{1-\alpha} e(x) \newline \tilde{J}(x) &= \sqrt{\rho’}\left( 1 - \alpha \frac{e(x)e^T(x)}{|e(x)|^2} \right) J(x) \end{align*} \tag{4.8} $$ 如果 $2\rho’’ |e(x)|^2 + \rho’ \lesssim0$ ,则我们限制 $\alpha < 1 - \varepsilon$ ,其中 $\varepsilon$ 为任意小量。
在 preMarginalize 函数计算每一因子残差与 Jacobian 矩阵的的时候,其中会有一段判断是否使用核函数的代码。相关代码段如下:(与 ceres-sover 中 corrector.cc 一致)
if (loss_function) {
double residual_scaling_, alpha_sq_norm_;
double sq_norm, rho[3];
sq_norm = residuals.squaredNorm();
loss_function->Evaluate(sq_norm, rho);
double sqrt_rho1_ = sqrt(rho[1]);
if ((sq_norm == 0.0) || (rho[2] <= 0.0)) {
residual_scaling_ = sqrt_rho1_;
alpha_sq_norm_ = 0.0;
} else {
const double D = 1.0 + 2.0 * sq_norm * rho[2] / rho[1];
const double alpha = 1.0 - sqrt(D);
residual_scaling_ = sqrt_rho1_ / (1 - alpha);
alpha_sq_norm_ = alpha / sq_norm;
}
for (int i = 0; i < static_cast<int>(parameter_blocks.size()); i++) {
jacobians[i] = sqrt_rho1_ * (jacobians[i] - alpha_sq_norm_ * residuals * (residuals.transpose() * jacobians[i]));
}
residuals *= residual_scaling_;
}
4.2 边缘化后求解先验因子的雅克比与残差
根据 Marginalization 知识3利用舒尔补求解先验因子。为了方便说明我们将计算过程公式展示如下:(需要注意的与 Sliding Window & Marginalization Part-23 4.1 的推导过程不同的是系统求解的状态增量) $$ \begin{align*} \begin{bmatrix} H _{mm} & H _{bm}^T \newline H _{bm} & H _{bb} \end{bmatrix} \begin{bmatrix} \delta\mathbf{x} _m \newline \delta\mathbf{x} _b \end{bmatrix} &= \begin{bmatrix} \mathbf{b} _m \newline \mathbf{b} _b \end{bmatrix} \newline \begin{bmatrix} I & 0 \newline -H _{bm} H _{mm}^{-1} & I \end{bmatrix} \begin{bmatrix} H _{mm} & H _{bm}^T \newline H _{bm} & H _{bb} \end{bmatrix} \begin{bmatrix} \delta\mathbf{x} _m \newline \delta\mathbf{x} _b \end{bmatrix} &= \begin{bmatrix} I & 0 \newline -H _{bm} H _{mm}^{-1} & I \end{bmatrix} \begin{bmatrix} \mathbf{b} _m \newline \mathbf{b} _b \end{bmatrix} \newline \begin{bmatrix} H _{mm} & H _{bm}^T \newline 0 & H _{bb} - H _{bm} H _{mm}^{-1} H _{bm}^T \end{bmatrix} \begin{bmatrix} \delta\mathbf{x} _m \newline \delta\mathbf{x} _b \end{bmatrix} &= \begin{bmatrix} \mathbf{b}_m \newline \mathbf{b} _b - H _{bm} H _{mm}^{-1} \mathbf{b} _m \end{bmatrix} \newline \text{得:} \quad \underbrace{(H _{bb} - H _{bm} H _{mm}^{-1} H _{bm}^T)} _{A} \delta \mathbf{x} _b &= \underbrace{\mathbf{b} _b - H _{bm} H _{mm}^{-1} \mathbf{b}_m} _{b} \end{align*} \tag{4.9} $$ 我们需要构建先验因子的雅克比矩阵与残差,用于后续优化的求解与迭代。由 $J^TJ \delta x = -J^Tr$ 可以得: $$ \begin{matrix} A = J^T J = VSV^T = VSV^{-1} = V \sqrt{S} \sqrt{S} V^T = (\sqrt{S}V^T)^T \sqrt{S}V^T \newline \to J = \sqrt{S}V^T \newline b = J^T r \to r = (J^T)^{-1}b = (V\sqrt{S})^{-1} b = \sqrt{S}^{-1}V^{-1}b = \sqrt{S}^{-1}V^T b \end{matrix}\tag{4.10} $$ 相对应的代码在 marginalize 函数中:
Eigen::VectorXd bmm = b.segment(0, m);
Eigen::MatrixXd Amr = A.block(0, m, m, n);
Eigen::MatrixXd Arm = A.block(m, 0, n, m);
Eigen::MatrixXd Arr = A.block(m, m, n, n);
Eigen::VectorXd brr = b.segment(m, n);
A = Arr - Arm * Amm_inv * Amr;
b = brr - Arm * Amm_inv * bmm;
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));
Eigen::VectorXd S_sqrt = S.cwiseSqrt();
Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;
4.3 边缘化先验因子残差更新
根据 Marginalization 求解先验因子,虽然边缘化后先验信息矩阵固定不变,但随着迭代的推进,变量不断优化,先验残差需要跟随变化。否则,求解系统可能崩溃。先验残差的变化可以用一阶泰勒近似: $$ \begin{align*} b_{prior} &= b + \frac{\partial b}{\partial x}\delta x = b + \frac{\partial(-J^T r)}{\partial x} \delta x = b - J^T \frac{\partial r}{\partial x} \delta x \newline &= b - J^TJ \delta x = b - A \delta x \newline \to \quad -J^T r’ &= -J^T r - J^T J \delta x \newline \to \quad r’ &= r + J \delta x \end{align*} \tag{4.11} $$ 由此在 MarginalizationFactor::Evaluate 函数中有
Eigen::Map<Eigen::VectorXd>(residuals, n) = marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx;