LSD: 线段检测器

LSD: a Line Segment Detector

LSD¹ 的目的是检测图像上的局部直线轮廓，就是我们所说的线段。轮廓是图像中的某些特殊区域，在这些区域，图像的灰度从黑到白或者从白到黑的剧烈变化。因此，图像的梯度和 level-lines (水平线) 是关键概念，如 Fig. 1 所示。

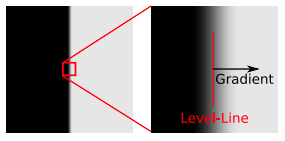
Fig. 1: Image gradient and level-lines.

该算法首先计算每个像素的 level-lines 角度，以产生一个 level-lines field (水平线场) ，即一个单位矢量场。该场依据 level-lines 角度被分割为连通的若干个部分，每个连通部分的 level-lines 角度方向近似相同并且在容忍度 $\tau$ 内，这样的连通部分被称之为 line support regions (线性支持域) ，如 Fig. 2 所示。

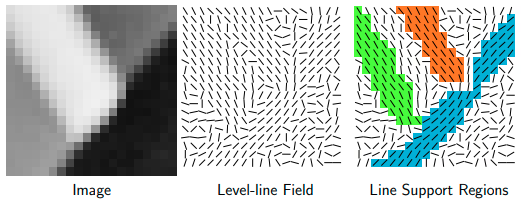
Fig. 2: Line Support Regions.

每个 line support regions （一组像素）都是线段检测的候选对象。同时，对于这个 line support region，可以关联一个最小外接矩形。并且 line support region 的主惯性轴被用作矩形的主要方向，矩形的大小被选择为覆盖整个区域，见 Fig. 3 。

Fig. 3: Rectangle approximation of line support region.

矩形中 level-line angle 与最小外接矩形的主方向的角度在容忍 (tolerance) $\tau$ 范围内对应的像素点，称为对 aligned point (齐点)，见 Fig. 4 。矩形中的像素点总数 $n$ 和对 aligned point 的数量 $k$ 被计算出来，将用于之后验证矩形是否能作为线段检测结果。

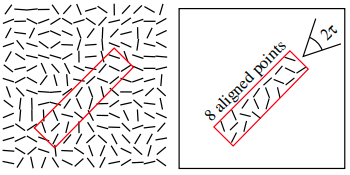
Fig. 4: Aligned points.

矩形是否能作为线段的验证方式是基于 Desolneux, Moisan 和 Morel 提出的 a contrario approach and the Helmholtz principle 。所谓 Helmholtz principle 指出，在一个有噪声的图像上不应该产生任何感知（或检测）。因此，相反的方法建议定义一个噪音或反向模型 $H_0$ ，其中不存在所需的结构。然后，如果在一个相反的模型上，与观察到的事件一样好的事件的预期数量很小，则事件被验证。换句话说，结构化事件被定义为在逆向模型中是罕见的。

矩形中在含有线段的情况下，我们对 aligned points 的数量感兴趣。我们考虑的事件是，在相反的模型中，线段有与观察到的线段一样多或更多的 aligned points 。给定一个图像 $i$ 和一个矩形 $r$ ，定义 $k(r, i)$ 表示矩形 $r$ 中 aligned points 的数量，$n(r)$ 表示矩形 $r$ 中所有像素点的数量。这样上述事件发生的次数即为 $$ N_{\rm test} \cdot P_{H_0} [k(r, I) \geq k(r, i)] \tag{1} \label{1} $$ 其中，测试次数 $N_{\rm text}$ 是正在考虑的可能的矩形的总数，$P_{H_0}$ 表示一个矩形对应的反向模型 $H_0$ 中 aligned points 数量不小于实际模型中 aligned points 数量的概率。$I$ 是遵循 $H_0$ 的随机图像。噪声模型 $H_0$ 固定了 aligned points 数量 $k(r, I)$ 的分布，它只取决于与 $I$ 相关的 level-line field 的分布。因此 $H_0$ 是图像梯度方向的噪声模型，而不是图像的噪声模型。

因此，用于线段检测的反向模型 $H_0$ 被定义为满足以下特性的水平线场的随机模型：

• $\lbrace LLA(j) \rbrace_{j\in{\rm Pixels}}$ 是由独立的随机变量组成的
• $\lbrace LLA(j) \rbrace$ 在 $[0, 2\pi]$ 上均匀分布

其中，$\lbrace LLA(j) \rbrace$ 是像素 $j$ 处的 level-line angle 。在假设 $H_0$ 下，反向模型上的像素是 aligned point 的概率为 $$ p = \frac \tau \pi \tag{2}\label{2} $$ 并且，由于随机变量 $LLA(j)$ 的独立性，$k(r, I)$ 遵循二项分布。因此，概率项 $P_{H_0}[k(r, I) \geq k(r, i)]$ 由以下公式给出 $$ P_{H_0} [k(r, I) \geq k(r, i)] = B \big( n(r), k(r,i), p \big) \tag{3} \label{3} $$ 其中 $B(n, k, p)$ 是由二项分布组合的： $$ B(n, k, p) = \sum_{j=k}^n \left( \begin{array}{c} n \newline j \end{array} \right) p^j(1-p)^{n-j} \tag{4} \label{4} $$ 测试的数量 $N_{\rm test}$ 为在固定精度下可以显示排列的矩形（直线）的总数。由于这些矩形是有方向性的，在 $N \times M$ 的图像中直线的起点和终点分别有 $N \times M$ 种选择。因此在一个 $N \times M$ 的图像中，这就得到了 $NM \times NM$ 不同的矩形。同时矩形有 $\sqrt{NM}$ 种不同的宽度值，见 Fig. 5

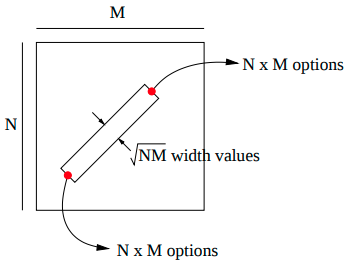
Fig. 5: Estimation of the number of tests.

因此，可以考虑的矩形数量为： $$ (NM)^{5/2} \tag{5} \label{5} $$ 起初 aligned point 的概率 $p$ 设置为 $\tau/\pi$ ，但是还有其他的测试值，以覆盖相关的值范围设 $\gamma$ 是可能尝试的不同 $p$ 值的数量，每个矩形的每个 $p$ 值都是一个不同的测试。因此，最终测试的数量 $N_{\rm test}$ 是 $$ (NM)^{5/2}\gamma \tag{6} \label{6} $$ 最后，我们定义与图像 $i$ 上的矩形 $r$ 相关的误报数 (Number of False Alarms, NFA) 为 $$ NFA(r, i) = (NM)^{5/2}\gamma \cdot B \big ( n(r), k(r, i), p \big) \tag{7} \label{7} $$ 这里用 NFA 来评判 observe img 中某个矩形 $r$ 小于 contrario model 中相同位置里 aligned points 的数量的概率，如果 NFA 的值很大，认为在观测图像中 aligned points 比 contrario model 中 aligned points 小的概率很大，将其认为是 common，平常的，背景中的一部分。如果 NFA 的值很小，认为目标是相对突出 (rare) 的，是一个合适的 “直线” 。选择一个阈值 $\varepsilon$，当一个矩形具有 $NFA(r, i) ≤ \varepsilon$ 时，它被称为 $\varepsilon \textit{-meaningful rectangle}$ 并产生检测。设定 $\varepsilon=1$ ，这相当于在逆向模型中每幅图像平均接受一次错误检测，这是合理的（具体证明见原论文）。

LSD 的整体算法如下所示：

LSD 算法将灰度图像作为输入，并返回一个检测到的线段列表。辅助图像 Status 的大小与缩放后的图像相同，用于跟踪已经使用的像素。LSD 被设计为一个自动图像分析工具。因此，它能够在不需要任何参数调整的情况下工作。下文将描述该算法的每一步。

图像缩放 - Image Scaling

为了解决数字离散图像的阶梯效应，如 Fig. 6 所示，两种情况的直线段检测结果是合情合理的，但是并非我们所希望看到的结果。Fig. 7 给出了缩小至原图的80%后再进行直线段检测的结果，两个边缘都被检测出来。

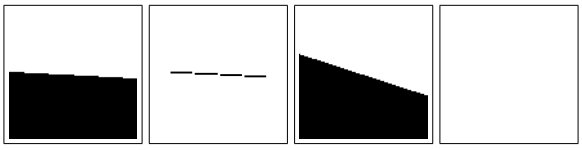
Fig. 6: Discrete edges at two angles and the detections without scaling.

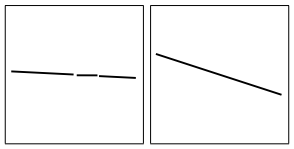
Fig. 7: Detections for the images in figure 6, but using scaling.

论文给出的缩放比例是原图像的 80%，即缩放后是尺寸是 $N \times M$ ，则缩放前是 $1.25N \times 1.25M$ ，缩放的方法用的是高斯降采样，而高斯核的标准差 $\sigma = \Sigma / S$，这里 $\Sigma$ 取值0.6，而 $S$ 取值0.8，可以在避免混叠和避免图像模糊之间获得良好的平衡。

梯度计算 - Gradient Computation

图像梯度是按照 $2\times2$ 的掩膜计算的，给出图像的局部灰度值如下图所示，

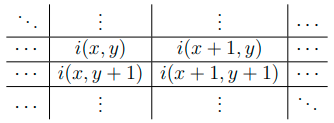
那么梯度计算如下， $$ \begin{align*} g_x(x,y) &= \frac{i(x+1, y) + i(x+1, y+1) - i(x,y) - i(x, y+1)}{2} \newline g_y(x,y) &= \frac{i(x, y+1) + i(x+1, y+1) - i(x,y) - i(x+1, y)}{2} \end{align*} \tag{8} \label{8} $$ 于是有 level-line angle 计算如下， $$ \arctan \bigg( \frac{g_x(x,y)}{-g_y(x,y)} \bigg) \tag{9} \label{9} $$ 那么梯度幅值为， $$ G(x,y) = \sqrt{g_x^2(x, y) + g_y^2(x, y)} \tag{10} \label{10} $$ 在计算中使用了尽可能小的掩码尺寸，从而尽可能地减少了计算出的梯度值的依赖性（因此，在噪声图像的情况下，接近理论上的独立性）。梯度和 level-line angle 编码了边缘的方向，也就是说，从暗到亮的过渡角度。请注意，从暗到亮的过渡和从亮到暗的过渡是不同的，两者在相应的梯度角或 level-line angle 之间有180度的角差。这意味着 LSD 检测到的结果线段是有方向性的，其起点和终点的顺序不是任意的。举例来说，当灰度图进行亮度翻转（将黑色改为白色，将白色改为黑色），LSD 的结果将是相同的，但每个线段的起点和终点将被交换。

梯度伪排序 - Gradient Pseudo-Ordering

LSD 是一种贪婪的算法，像素的处理顺序对结果有影响。梯度值越大，越是显著的边缘点，更适合作为种子点。但是对梯度值进行完全排序是一个时耗性很高的工作。排序算法通常需要 $O(\textit{n log n})$ 操作来对 $n$ 个值进行排序。然而，简单的像素伪排序在线性时间内是可能的。为了达到这个目的，简单的将梯度值划分为 1024 个等级 (bins) ，对应于图像上零到最大观测值之间的相等梯度区间。像素根据其梯度大小被分类到对应的等级内。LSD 首先使用梯度最大的仓中的种子像素，然后从第二个仓中提取种子像素，以此类推，直到所有的仓都用完。

梯度阈值 - Gradient Threshold

梯度值小的像素对应于图像中平滑或者变化较缓的区域，而它们在量化时将会引起更大的梯度计算误差。在 LSD 算法中，通过设置梯度阈值 $\rho$ ，梯度值小于 $\rho$ 的点不会在线支持区域和矩形中使用。假设量化噪声为 $n$ ，一个图像为 $i$ ，那么就有观测值： $$ \tilde i = i+n \quad \nabla \tilde i = \nabla i + \nabla n \tag{11} \label{11} $$ 于是角度误差 （见 Fig. 8） $$ |\text{angle error}| \leq \arcsin \Big( \frac q{|\nabla i|} \Big) \tag{12} \label{12} $$ 其中，$q$ 是 $|\nabla n|$ 的边界，所用的标准是拒绝那些角度误差大于区域增长算法中使用的角度容限 $\tau$ 的像素。也就是说，要使得 $|\text{angle error}| \leq \tau$ ，有 $$ \rho = \frac q {\sin \tau} \tag{13} \label{13} $$

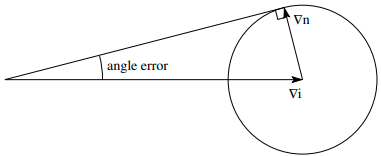
Fig. 8: Estimation of the angle error due to quantization noise.

在通常情况下，像素值被量化为 $\lbrace 0,1,\dots,255 \rbrace$ 中的整数值。 因此，梯度的最大可能误差是 1（当相邻像素的量化误差为 0.5 时，不能进行补偿）。由于经验上的原因，倾向于一个更保守的界限，设定 $q = 2$ 。

区域生长 - Region Growing

LSD 算法的区域生长跟我们以往所了解的区域生长算法原理大致相同，它利用伪排序得到的排序列表中梯度幅值大的点作为种子点，以该点的水平线角度作为区域的初始角度 $\theta_{region}$ ，然后在八邻域中寻找与 $\theta_{region}$ 的偏差小于容忍值 $\tau$ 的点，然后将该点加入到区域中并更新 $\theta_{region}$ ，更新方式为

$$ \arctan \bigg( \frac{\sum_j \sin(\text{level-line-angle} _j)}{\sum_j \cos(\text{level-line-angle} _j)} \bigg) \tag{14} \label{14} $$

上式中 $j$ 遍历区域中的所有点。当区域中所有点的八邻域中都不满足与 $\theta_{region}$ 的偏差小于容忍值 $\tau$ 时，此时停止生长，算法的处理过程如下图所示。

角度容忍度 $\tau$ 设置为 22.5 度,或者说 $\pi/8$ 弧度。在该误差容忍度范围内的像素点都将被选择到矩形中，这是因为他们在很大程度上跟矩形的方向保持一致。 如 Fig. 9 所示，实验发现，22.5 是一个较好的参数。

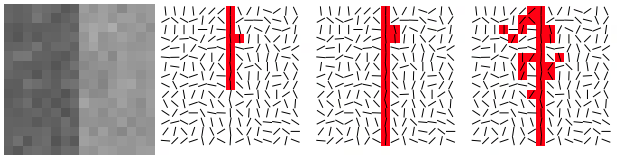
Fig. 9: Examples of region growing starting at the middle top pixel for three values of the angle tolerance. From left to right: $\tau = 11.25; \tau = 22.5; \tau = 45$

矩形估计 - Rectangular Approximation

上一步形成了 line-support region 一系列相邻的离散点，对每一个 line-support region 在验证之前，需要先进行一次矩形逼近，构造一个特定的包含区域中所有点的矩形。构造的原理为：首先把整个区域当做一个实体，而区域中每个像素点的梯度大小为点的质量，这样整个实体就有一个质心，将质心作为矩形的中心点。假设区域中每个点的坐标为 $(x(j), y(j))$ ，对应的质量为 $G(j)$ ，那么矩形的中心 $(c_x, c_y)$ 为：

$$ \begin{align*} c_x &= \frac{\sum_{j\in{\rm Region}} G(j) \cdot x(j)}{\sum_{j\in{\rm Region}} G(j)} \newline c_y &= \frac{\sum_{j\in{\rm Region}} G(j) \cdot y(j)}{\sum_{j\in{\rm Region}} G(j)} \end{align*} \tag{15} \label{15} $$

然后确定矩形的朝向角度，其角度设置为与矩阵 $M$ 的最小特征值相关联的特征向量的角度。 $$ M = \begin{bmatrix} m^{xx} & m^{xy} \newline m^{xy} & m^{yy} \end{bmatrix} \tag{16} \label{16} $$ 其中，$m^{xx}, m^{yy}， m^{xy}$ 的值分别为：

$$ \begin{align*} m^{xx} &= \frac{\sum_{j\in{\rm Region}} G(j) \cdot (x(j) - c_x)^2}{\sum_{j\in{\rm Region}} G(j)} \newline m^{yy} &= \frac{\sum_{j\in{\rm Region}} G(j) \cdot (y(j) - c_y)^2}{\sum_{j\in{\rm Region}} G(j)} \newline m^{xy} &= \frac{\sum_{j\in{\rm Region}} G(j) \cdot (x(j) - c_x)(y(j) - c_y)}{\sum_{j\in{\rm Region}} G(j)} \end{align*} \tag{17} \label{17} $$

确定了矩形的中心和矩形的朝向后，包含区域所有点的最小矩形即为逼近得到的矩形。

NFA 计算 - NFA Computation

根据上文中详细的介绍，结合式 $\eqref{2},\eqref{3},\eqref{4},\eqref{5},\eqref{6},\eqref{7}$ 有 $$ \begin{align*} NFA(r) &= (NM)^{5/2}\gamma \cdot \sum_{j=k}^n \left( \begin{array}{c} n \newline j \end{array} \right) p^j(1-p)^{n-j} \newline \text{with} \quad \left( \begin{array}{c} n \newline j \end{array} \right) &= \frac{\Gamma(n+1)}{\Gamma(k+1) \cdot \Gamma(n-k+1)} \end{align*} \tag{18} \label{18} $$ 其中，$\Gamma$ 为 Gamma 函数 。

齐点密度 - Aligned Points Density

在某些情况下，这 $\tau$ 角度容忍度的方法产生一个错误的结果。当图像中存在两条直边，它们之间形成的角度小于公差 $\tau$ 时，就会出现这个问题。Fig. 10 显示了一个待检测 line-support region 的例子（灰色）和与之对应的矩形。

Fig. 10: A problem that can arise at the regions growing process.

在 LSD 中，这个问题是通过检测有问题的 line-support region 并将其切割成两个较小的区域来处理的，希望在适当的位置将该区域分割出来以解决问题。这个 “角度问题” 的检测是基于矩形中 aligned points 的密度。当这个问题不存在时，矩形非常适合于 line-support region ，并且同性点的密度很高。另一方面，当 “角度问题” 出现时，正如前面的图所看到的， aligned points 的密度很低。同样，当一个稍微弯曲的边被一系列直边近似地逼近时，近似的程度（多少线段被用来覆盖曲线的一部分）与 aligned points 的密度有关；因此， aligned points 密度也与线段近似曲线的精度有关。

对于一个线支持区域和对应的逼近矩形 $r$ ，区域中 aligned points 的数量为 $k$ ，那么该矩形的 aligned points 密度为 $$ d = \frac{k}{{\rm length}(r) \cdot {\rm width}(r)} \tag{19} \label{19} $$ 规定一个阈值 $D$ ，在这里设置 $D=0.7$ ，文章认为这个数字既能保证同一个 $r$ 中的 aligned points 属性相近，也能保证 $r$ 不会被过分的分割为小的矩形。若 $d > D$（ aligned points 密度阈值）则保留。否则，需要将 $r$ 截断。 $r$ 截断的方法有两种：“缩小角度误差阈值” 与 “缩小区域半径” 的方法。在这两种方法中，区域中的一部分像素被保留，而另一些则重新标记为 NOT USED ，因此它们可以在将来的线支持区域中再次使用。

• 缩小角度容忍阈值：简单的将 $\tau$ 值缩小，再次从当前 $r$ 的 seed 开始搜寻，看是否满足要求。

• 缩小区域半径：逐渐去除远离种子的像素，直到满足标准或区域太小而被拒绝为止。当线支持区域对应于一条曲线时，该方法效果最好，并且在满足密度准则之前需要减少区域，通常意味着对曲线有一定程度的近似。

矩形改善 - Rectangle Improvement

为了获得更准确的矩形检测结果，需要改善所有的矩形，这也包括的矩形，改善分为以下五个步骤：

1. 尝试较小 precision 的值，设初始值为 $p$，分别取 $p,\frac{p}{2},\frac{p}{4},\frac{p}{8},\frac{p}{16},\frac{p}{32}$
2. 尝试同时减少矩形的宽，设初始值为 $W$, 分别取 $W,W-0.5,W-1,W-1.5,W-2,W-2.5$
3. 尝试只减少矩形的长边，设初始值为 $a$，分别取 $a,a-0.5,a-1,a-1.5,a-2,a-2.5$
4. 尝试只减少矩形的短边，设初始值为 $b$，分别取 $b,b-0.5,b-1,b-1.5,b-2,b-2.5$
5. 尝试更小的 $p$ 值，包括 $\hat p,\frac{\hat p}{2},\frac{\hat p}{4},\frac{\hat p}{8},\frac{\hat p}{16},\frac{\hat p}{32}$ ，其中 $\hat p$ 为第一步中最小的 NFA 值对应的 $p$ 值

以上五个步骤最后只保留最小的 NFA 所对应的变量值。从上述可知，对 precision 的取值共有 11 个，因此计算NFA时，$\gamma = 11$ 。

Reference ^{2 3}