基于 LBD 描述子和成对几何一致性的高效鲁棒线段匹配方法

An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency

特征匹配是计算机视觉领域具有挑战性的领域之一，是场景重建、模式识别和检索、 SLAM 等应用的基本工具。现有文献中的大多数匹配方法都是基于局部点或区域特征，这对于低纹理场景是有缺陷的。相反，在这些情况下，线特征特征通常很丰富。此外，线段特征和其他局部特征可以提供互补的场景信息。因此，线段匹配在许多应用中既是可取的也是不可或缺的。文章¹提出了一种解决稳健高效的线段特征匹配问题的算法。

线匹配成为一个难题的原因有：线端点位置不准确、线碎片、缺乏强烈消除歧义的几何约束（例如极线约束）、低纹理场景中缺乏独特的外观、大型图像变换的不稳定。为了应对这些挑战，文章提出的方法基于三种策略：1）提取尺度空间中的线，使匹配算法对尺度变化具有鲁棒性； 2）通过线带描述符 (LBD) 来表征线段的局部外观，该描述符的计算效率比 MSLD (Mean-Standard deviation Line Descriptor) 更高效； 3）结合线的局部外观和线对之间的几何约束来构建关系图。 通过检查外观相似性和几何一致性来降低图匹配问题的维数。所提出的线匹配方法可以更快地生成匹配结果。 即使对于非平面场景或低纹理场景，它也能抵抗各种图像变换，包括遮挡、旋转、模糊、照明变化、比例变化和适度的视点变化。

1. 线段检查与描述 - Line detection and description

在本节中，首先介绍在尺度空间中检测线段的方法。 然后介绍构建线条段描述符的方法。

1.1 在尺度空间内提取线段 - Detecting lines in the scale space

为了克服线段检测的碎片化问题，并提高大尺度变化时的性能，在线检测框架中采用了由 N 个倍频图像组成的尺度空间金字塔。这些图像是通过使用一组比例因子和高斯模糊对原始图像进行下采样而生成的。两个连续倍频程之间没有内层。先对每个倍频层应用 EDLine 算法，在尺度空间中生成一组线。 每条线都有一个方向，该方向是通过使大多数边缘像素的梯度从线的左侧指向其右侧而给出的。 然后通过在尺度空间中找到相应的线来重新组织它们。对于每一个从尺度空间里取出的线段，如果它们在图像中是相同的线段，但是在不同的尺度空间里，都将安排一个唯一 ID 并将其存入到同一个 LineVec 变量中。如 Fig. 1 所示，最终提取的结果是一组 LineVec 。因为重新组织的尺度空间中的线段特征为 LineVec，所以这减少了图匹配问题的维度。同一个 LineVec 中的不同的线段，指的是不同尺度空间下的同一个线段。所以在同一个 LineVec 下的线段都拥有相同的方向，并且对应于原图的同一个区域。

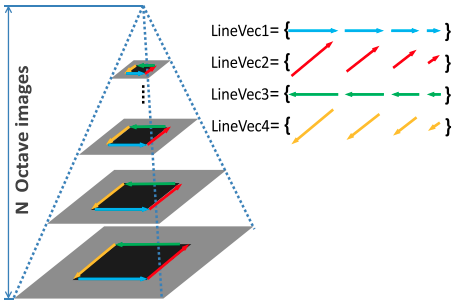
Fig. 1: 尺度空间中的线检测的图示。 对原始图像进行向下采样，生成一组倍频程图像。对于每个倍频程图像，使用 EDLine 检测器提取线段。对所有提取的线段进行重新组织，形成一组 LineVec。同一 LineVec 中的线条具有相同的方向，并与原始图像中的相同区域相对应。

1.2 线段支持域的条带表示方法 - The band representation of the line support region

在 octave image 给定的一个线段，描述符将从线段支持域（line support region, LSR）计算，该区域是一个以线为中心的局部矩形区域，如 Fig. 2 所示。该支持区域被划分为一组条带 $\lbrace B_1,B_2,\cdots, B_m \rbrace$ ，每个条带都是 LSR 的子区域并且它们与线段是平行的，条带的数量 $m$ 的和每个条带的宽度 $w$ ，条带的长度等于线段的长度， Fig. 2 举例说明了当 $m=5 , w=3$ 时的 LSR 区域图。

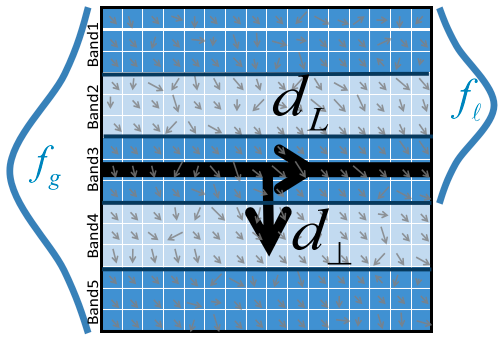
Fig. 2: 选择线周围的局部矩形区域作为线段支持域（LSR）。引入两个方向 ${\bf d} _L$ 和 ${\bf d} _\bot$ 。LSR 被划分为 $m$ 个带，宽为 $w$ 的区域（例如 $m = 5, w = 3$）。全局高斯函数 $f_g$ 适用于 LSR 中的所有行。对于每个条带（例如 Band2），一个局部高斯函数 $f_l$ 应用于该波段及其最近两个相邻波段的行。小箭头代表 LSR 中像素的梯度。

与 MSLD 类似，为了区分梯度方向相反的平行线并使描述符旋转不变，引入了构成局部二维坐标框架的两个方向。根据直线方向 ${\bf d} _L$ ，正交方向 ${\bf d} _\bot$ 被定义为 ${\bf d} _L$ 的顺时针正交方向。选取直线的中点作为局部坐标系的原点。LSR 中每个像素的梯度被投影到这个局部坐标系中 ${\bf g}’ = ({\bf g}^T \cdot {\bf g} _\bot , {\bf g}^T \cdot {\bf g} _L) \triangleq ({\bf g}’ _{d _\bot} , {\bf g}’ _{d _L})$ 中，其中 ${\bf g}$ 和 ${\bf g}’$ 分别是像素在图像坐标系和局部坐标系中的梯度。

受 SIFT 和 MSLD 的启发，沿 ${\bf d} _\bot$ 方向的 LSR 的每一行应用两个高斯函数。首先，在 LSR 内的第 $i$ 行上安排一个全局权重系数 $f_g(i) = (1 / \sqrt{2\pi} \sigma_g)e^{-d_i^2 / 2 \sigma_g^2}$ ，其中 $d_i$ 表示 LSR 中第 $i$ 行到中心行的距离，并且 $\sigma_g = 0.5(m \cdot w -1)$ 。其次，对于 $B_j$ 条带和它的相邻条带 $B _{j-1}$ 和 $B _{j+1}$ 中的每一行，给第 $k$ 行分配一个局部加权系数 $f_l(k) = (1/\sqrt{2\pi} \sigma_l)e ^{-d_k’ / 2 \sigma_l^2}$ ，其中 $d_k’$ 是第 $k$ 行到 $B_j$ 条带中心行的距离，并且 $\sigma_l = w$ 。全局高斯窗的目的是为降低远离线段的梯度的重要性，以此缓和在线段垂直方向 ${\bf d} _\bot$ 上微小变化的敏感度。局部高斯窗的目的是为降低边缘效应，避免了像素从一个条带到下一个条带时，描述符突然改变。

该描述子有两个优点：首先，它对 ${\bf d} _\bot$ 上的细小位置变化更具有鲁棒性，因为在这个方法中，条带边界的微小变化时，条带内的大部分图像内容依然保持不变。这一特性非常重要，因为通常情况下，由于线段端点的不稳定性，一条线在 ${\bf d} _L$ 方向的位置精度比 ${\bf d} _\bot$ 方向要低。其次，由于 ${\bf d} _L$ 方向条带间没有重叠部分，所以其计算效率更高，并且高斯权重直接应用于每一行像素，而非每一个像素。

1.3 构造条带描述符 - The construction of the Line Band Descriptor

定义出了线段的条带之后，就可以构造条带描述符了。对于 LSR 中的条带 $B_j$ ，其对应条带描述符 $BD_j$ 是通过 $B_j$ 和它的两个相邻条带 $B _{j-1}$ 和 $B _{j+1}$ 构成的。 特别地，在计算条带中顶端条带 $B_1$ 和和底端条带 $B_m$ 时，在 LSR 区域以外的部分不考虑到算法中。在计算完 $BD_j$ 之后，通过连接它们即可简单生成线带描述符 LBD：

$$ {\rm LBD} = (BD_1^T, BD_2^T, \dots , BD_m^T) \tag{1} \label{1} $$

对于第 $k$ 行中的条带描述符 $BD_j$ ，累计该行中四个方向上像素的梯度，分别是 ${\bf d} _\bot$ 方向，${\bf d} _\bot$ 反方向， ${\bf d} _L$ 方向， ${\bf d} _L$ 反方向：

$$ \begin{align*} \nu1_j^k &= \lambda \sum _{{\bf g} _{d _\bot}’ > 0} {\bf g} _{d _\bot}’ & \nu2_j^k &= \lambda \sum _{{\bf g} _{d _\bot}’ < 0} {\bf g} _{d _\bot}’ \newline \nu3_j^k &= \lambda \sum _{{\bf g} _{d _L}’ > 0} {\bf g} _{d _L}’ & \nu4_j^k &= \lambda \sum _{{\bf g} _{d _L}’ < 0} {\bf g} _{d _L}' \end{align*} \tag{2}\label{2} $$

其中，$\lambda = f_g(k)f_l(k)$ 是高斯系数，所以一行像素我们总结出4个方向的梯度数据。将与频带 $B_j$ 相关的所有行的这四个累积梯度堆叠起来，就构建出了条带描述矩阵 (the band description matrix, BDM)：

$$ BDM_j = \left(\begin{matrix} \nu1_j^1 & \nu1_j^2 & \cdots & \nu1_j^n \newline \nu2_j^1 & \nu2_j^2 & \cdots & \nu2_j^n \newline \nu3_j^1 & \nu3_j^2 & \cdots & \nu3_j^n \newline \nu4_j^1 & \nu4_j^2 & \cdots & \nu4_j^n \end{matrix}\right) \in \mathfrak R^{4\times n} \tag{3} \label{3} $$ 其中，数字 $n$ 是行数，由于存在边缘条带，所以 $n$ 的定义为 $n=\begin{cases} 2w, & j=1||m \newline 3w, & else \end{cases}$ 。

$BD_j$ 由 $BDM_j$ 矩阵的均值向量 $M_j$ 和标准方差 $S_j$ 得到 ${\rm LBD} = (M_1^T, S_1^T, M_2^T, S_2^T, \dots, M_m^T, S_m^T) \in \mathfrak R^{8m}$ 。然后对LDB的均值部分和标准方差部分分别进行归一化，因为他们大小不同。并且为了减小非线性光照的影响，对每个 LBD 维度进行约束，使它小于一个阈值（经验：0.4 的是一个很好的值）。最后我们重新归一化约束向量得到一个单元 LBD 。

2. 利用频谱法进行图匹配 - Graph matching using spectral technique

上一步我们进行了线特征的检测和描述之后，接下来进行线特征的匹配。下面将介绍构造两组 LineVecs 之间的关系图并且在图中建立匹配结果的方法。在此之前先通过预处理将一些明显无法匹配的特征给消除，以降低图匹配问题的维度。

2.1 生成候选匹配对 - Generating the candidate matching pairs

匹配的双方，分别称为参考图像和查询图像，检测出双方的 LineVecs 之后，要检测它们的一元几何属性和局部外观相似度，若未通过测试，那么认为它们是不匹配的。这样做可以大大减小图优化匹配的问题维度，使得后期匹配的速度更快。

2.1.1 一元几何属性 - Unary Geometric Attribute

线段的一元几何属性就是 LineVecs 的方向，在同一个 LineVec 中的线具有相同的方向，并且每一个 LineVec 拥有唯一的方向。图像对中对应 LineVec 的方向是模糊和不可靠的，因为图像对可以有任意的旋转变化。 尽管这确实是事实，但图像对之间往往存在一个近似的整体旋转角度。只要有这个属性，就可以利用它来减少候选匹配的数量。

和其他文章中通过点特征对应匹配来确定图像之间的近似旋转关系不同， LBD 的 Matching 中直接计算参考图像和查询图像的 LineVec 方向直方图。然后得到归一化直方图 $({\bf h} _r, {\bf h} _q)$ ，其中下标 $r$ 表示参考图像，$q$ 表示查询图像。然后，将 ${\bf h} _q$ 移动一个从 $0$ 到 $2\pi$ 不等的角度。通过 $\eqref{4}$ 寻找一个全局近似旋转角 $\theta_g$ $$ \theta_g = \underset{0 \leq \theta \leq 2\pi}{\arg\min} \lVert {\bf h} _r(x) - {\bf h} _q(x - \theta) \rVert \tag{4}\label{4} $$ 而全局旋转变换不一定总是好的，所以也需要去检查估计旋转角是不是真的。实际上如果透视变换可以通过旋转来近似，那么直方图之差 $\lVert {\bf h} _r(x) - {\bf h} _q(x - \theta) \rVert$ 比较小。这代表了在进行了旋转之后，两个图像之间的相似程度。Fig. 3 就显示出了两张图之间的直方图差距，通过旋转可以得出两张图之间相似度很高。上图中的预估角度 $\theta_g$ 是 0.349 rad，偏移的直方图距离是 0.243 。

Fig. 3: 前两幅图像分别是检测到线段的参考图像和查询图像，最右图显示的是它们的方向直方图。每个分区的分辨率为 20，因此每个直方图有 18 个分区

但是如果图像中提取的线重复度很低的话，这种直方图方法就有可能提取出错误的旋转角度。为了提高这种方法的鲁棒性，对于在方向直方图上落入相同区间 bins 的线段，将他们的长度累积起来。那么就可以得到一个长度向量，其第 $i$ 个元素就是方向直方图中第 $i$ 个 bin 中的线段累计长度。当最小偏移直方图距离小于阈值 $t_h$ ，并且最小偏移长度向量距离小于阈值 $t_l$ 时，接受所估计的全局旋转角。一旦全局旋转角 $\theta_g$ 被接受，就会有一对 LineVecs 被匹配。但是如果这对 LineVecs 的方向角度和估计的全局旋转角之差超过阈值 $|\alpha - \theta_g|>t_\theta$ ，$\alpha$ 是它们的方向之间的夹角，那么认为它们是不能够匹配的。如果两个图片之间没有可以接受的旋转角度，那么只测试它们的外观相似性。

2.1.2 局部外观相似性 - Local Appearance Similarity

用直线描述符之间的距离（lost）来度量局部外观相似度。对于 LineVec 中的每个线段，都从提取出线的尺度层中生成一个 LBD 描述子向量 $V$ 。当对一幅图像中提取出来的两组 LineVec 进行匹配，要去评估参考 LineVec 和测试 LineVec 中所有描述子之间的距离，并且用最小的描述子距离去测量 LineVec 外观相似度 $s$ 。如果 $s > t_s$ ，大于局部外观不相似容忍度 $t_s$ ，那么相应两个 LineVecs 将不会再进一步考虑。在检查了 LineVecs 的一元几何属性和局部外观相似性之后，通过了这些测试的直线对被当做候选匹配。在上面的测试中，应当选取一组松散阈值，其中经验值是 $t_θ=\pi/4, t_s=0.35$ 。候选匹配的数量比实际匹配的数量要大很多，因为不能仅仅按照刚才两个属性来确定最终的匹配结果，当然上面的工作也是大大减小了图形匹配的问题维度的。

2.2 构建关系图 - Building the relational graph

对于一组候选匹配项，建立一个关系图，其中关系图里的节点代表潜在的对应关系，节点之间的链接的权重代表它们之间的配对一致性。给定一组k候选匹配，关系图被一个大小为 $k\times k$ 的邻接矩阵 $A$ 表示，其中第 $i$ 行第 $j$ 列的元素值是候选 LineVec 匹配对 $(L_r^i, L_q^i)$ 和 $(L_r^j, L_q^j)$ 的一致性得分。其中 $L_r^i, L_r^j$ 和 $L_q^i, L_q^j$ 分别为引用图和查询图的 LineVecs 变量，上面的一致性得分是通过候选匹配对的成对几何属性和外观相似度计算的来的。

为了描述两 LineVecs $(L^i, L^j)$ 的成对集合特征，选择两条线 $(l^i, l^j)$ ，它们代表了这两个 LineVecs 之间的最小描述子距离，并在原图中定位它们的端点位置。随后，用它们的交点比率 $(I^i, I^j)$ ，投影比率 $(P^i, P^j)$ 和相对角度 $\Theta^{ij}$ 来描述 $(l^i, l^j)$ 的几何属性，如 Fig. 4 所示。

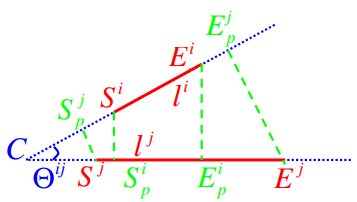
Fig. 4: 成对几何属性图解。$C$ 是两条直线的交点。$(S^i, E^i)$ 是线 $l^i$ 的端点，$(S^i_p, E^i_p)$ 是它们在直线 $l^j$ 上的投影。同样， $(S^j, E^j)$ 是线 $l^j$ 的端点，$(S^j_p, E^j_p)$ 是它们在直线 $l^i$ 上的投影

其中的两个值计算方法如下： $$ I^i = \cfrac{\overrightarrow{S^i C} \cdot \overrightarrow{S^iE^i}}{|\overrightarrow{S^iE^i}|^2} \qquad P^i = \cfrac{|\overrightarrow{S^i S_p^i}| + |\overrightarrow{E^i E_p^i}|}{|\overrightarrow{S^i E^i}|} \tag{5} \label{5} $$ 另 $I^j, P^j$ 的值可以利用相同的方法求解得到，$\Theta^{ij}$ 相对角度可以直接用线方向求得。这三个属性对于平移旋转缩放都是不变的。同上文，使用 LBD 描述向量来表示线的局部外观。假设描述子与 r 图（参考图）和 q 图（查询图）的 LineVecs $(L^i_r, L^i_q)$ 之间的最小距离是 $(V_r^i, V_q^i)$ ，同理对 $(L^j_r, L^j_q)$ 是 $(V_r^j, V_q^j)$ 。由此可以得到两组成对几何属性和局部外观，分别是 $\lbrace I_r^i, I_r^j, P_r^i, P_r^j, \Theta_r^{ij}, V_r^i, V_r^j \rbrace$ 和 $\lbrace I_q^i, I_q^j, P_q^i, P_q^j, \Theta_q^{ij}, V_q^i, V_q^j \rbrace$ 。计算一致性得分 $A^{ij}$ 为： $$ \begin{align*} &A^{ij} = \begin{cases} 5 - d_I - d_P - d_\Theta -s_V^i - s_V^j, & \text{if }\Gamma \text{ is true} \newline 0, & \text{else} \end{cases} \newline &\begin{cases} d_I = \min(\cfrac{|I_r^i - I_q^i|}{t_I}, \cfrac{|I_r^j - I_q^j|}{t_I}) \newline d_P = \min(\cfrac{|P_r^i - P_q^i|}{t_P}, \cfrac{|P_r^j - P_q^j|}{t_P}) \newline d_\Theta = \cfrac{|\Theta_r^{ij} - \Theta_q^{ij}|}{t_\Theta} \newline s_V^i = \cfrac{\lVert V_r^i - V_q^i \rVert}{t_s} \newline s_V^j = \cfrac{\lVert V_r^j - V_q^j \rVert}{t_s} \newline \Gamma \equiv \lbrace d_I, d_P, d_\Theta, s_V^i, s_V^j \rbrace \leq 1 \end{cases} \end{align*} \tag{6} \label{6} $$ 其中，$d_I, d_P, d_\Theta$ 是几何相似性，$s_V^i, s_V^j$ 是局部外观相似性，$\Gamma$ 是条件。最后一个代表所有在 $\Gamma$ 内的元素都不能大于 1 。设置 $t_I = 1, t_P = 1, t_\Theta = \pi/4, t_s = 0.35$ ，对于所有候选匹配，计算它们之间的一致性得分，并获邻接矩阵 $A$ 。为了获得更好的结果，建议 $A$ 对角线上的元素为 0 ，并且 $A^{ji} = A^{ij}$ 保持对称性。

2.3 生成最终匹配结果

匹配的问题现在简化为寻找匹配簇 $\mathcal{LM}$ 最大化总的一致性得分 $\sum _{(L_r^i, L_q^i),(L_r^j,L_q^j)\in \mathcal{LM}} A^{ij}$ ，以至于可以满足映射约束。使用一个指标向量来表示这个簇 $x(i) = 1 \text{ if } (L_r^i, L_q^i) \in \mathcal{LM}$ ，否则为 0 。因此这个问题被表示为： $$ x^* = \arg\max(x^TAx) \tag{7} \label{7} $$ 其中 $x$ 受限于映射约束。一般来说使用二次规划来解决这个这个问题太耗费资源，采用频谱法，对 $x$ 放宽的映射约束和积分约束，使得它的元素可以在采取实际值 $[0,1]$ 之间。通过 Raleigh 比率定理，可以最大化 $x^TAx$ 的 $x^*$ 是 $A$ 的主特征向量。它仍然是使用映射约束二值化特征向量和获得最优解的一个强大近似。

算法详细步骤如下：

1. 通过 EDLine 算法从参考图和查询图内提前 LineVecs ，以从两幅图中分别获取两组 LineVecs $\mathcal L_r$ 和 $\mathcal L_q$
2. 利用两组 LineVecs $\mathcal L_r$ 和 $\mathcal L_q$ 的方向直方图估计图像对的全局旋转角 $\theta_g$
3. 计算两组 LineVecs $\mathcal L_r$ 和 $\mathcal L_q$ 的 LBD 描述子
4. 通过检查描述子的一元几何属性和局部外观，生成一组候选匹配对 $\mathcal{CM} = \lbrace (L_r^1, L_q^1), (L_r^2, L_q^2), \dots, (L_r^k, L_q^k) \rbrace$
5. 根据候选匹配对 $\mathcal{CM}$ 中的一致性分数，构建 $k\times k$ 大小的邻接矩阵 $A$
6. 通过使用 ARPACK 库，得到邻接矩阵 $A$ 的主特征向量 $x^*$
7. 初始化匹配结果 $\mathcal{LM} \gets \emptyset$
8. 寻找 $a = \underset{1\leq i \leq M}{\arg\max} (x^* (i))$ ，如果 $x^* (a) = 0$ ，那么停止查找匹配结果 $\mathcal{LM}$ ，否则设 $\mathcal{LM} = \mathcal{LM} \cup \lbrace (L_r^a, L_q^a) \rbrace, \mathcal{CM} = \mathcal{CM} - \lbrace (L_r^a, L_q^a) \rbrace$ 且 $x^* (a) = 0$
9. 检查 $\mathcal{CM}$ 中所有的候选者，如果 $(L_r^j, L_q^j)$ 和 $(L_r^a, L_q^a)$ 冲突，那么设 $\mathcal{CM} = \mathcal{CM} - \lbrace (L_r^j, L_q^j) \rbrace$ 且 $x^*(j) = 0$
10. 如果 $\mathcal{CM}$ 是空的，那么返回 $\mathcal{LM}$ ，否则返回步骤 8

最后的线段匹配可以从 LineVecs $\mathcal{LM}$ 的匹配结果直接检索。注意，在 LineVec 的线位于图像的同一区域，并且具有同一方向，因此，对于每对 LineVec 的匹配，线段匹配有一对就足够检索了。

Reference ^{2 3}