IMU Preintegration factor In VINS

对于一个基于非线性图优化且利用滑动窗口固定计算量的紧耦合视觉惯导里程计，在求解 Bundle Adjustment 里有一项 IMU 预积分测量残差项（点击这里）。VINS-Mono¹ 中 IMU 预积分的算法可以参照该文章²。在 VINS 系统里 IMU 约束因子如下：

• 残差项 = 估计值 - 观测值
  • 观测值: IMU 预积分得到的位置、速度、姿态、bias（PVQB）的变化量，为观测值
  • 估计值：根据优化变量计算出来的两帧之间 PVQB 的变化量，为估计值
• 优化变量：第 1 帧和第 2 帧的 PVQB
• 协方差：IMU 预积分得到的协方差

在 VINS 的代码中 IMU 约束因子拆分到两个文件中，分别是 integration_base.h 与 imu_factor.h，分别对应于 IMU 测量预积分与后端残差雅克比估计。由此，下文也将分为两个章节来介绍。由于 VINS 系统中的姿态采用四元素进行表示，这部分可以参考³⁴，下文中用到的一些公式将不再进行推导。本文中的一些推导过程参考了⁵⁶。

1. IMU 预积分

1.1 IMU 测量方程

在 VINS 中 IMU 的测量方程建模如下： $$ \begin{align*} \hat a_t &= a_t + b_{a_t} + R_w^t g^w + n_a \newline \hat w_t &= w_t + b_{w_t} + n_w \end{align*}\tag{1.1}\label{1.1} $$ 加速度测量值与陀螺仪测量值分别为 $\hat a_t$ 和 $\hat w_t$ ，它们被关联在 IMU 坐标系。其中加速度测量值将叠加姿态影响下的重力且受加速度 bias 和测量噪声影响；陀螺仪测量值受陀螺仪 bias 和测量噪声影响。其中我们将噪声模型化为零均高斯噪声 $n_a \sim \mathcal N(0, \sigma_a^2), \ n_w \sim \mathcal N(0, \sigma_w^2)$ 。加速度与陀螺仪的 bias 利用随机游走进行模型化，它们的倒数是一个高斯分布，$n_{b_a} \sim \mathcal N(0, \sigma_{b_a}^2), \ n_{b_w} \sim \mathcal N(0, \sigma_{b_w}^2)$ : $$ \dot b_{a_t} = n_{b_a}, \quad \dot b_{w_t} = n_{b_w} \tag{1.2}\label{1.2} $$

1.2 IMU 预积分

IMU 预积分过程如下图所示，

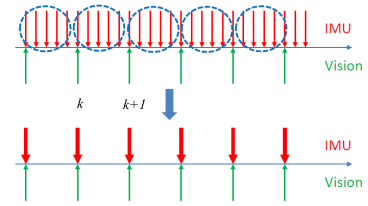
1.2.1 当前时刻在世界坐标系下连续形式 IMU 积分

给定对应图像帧 $b_k$ 和 $b_{k+1}$ 的两个时刻，K+1 时刻的位置、速度和姿态（PVQ）可以通过将 $[k, k+1)$ 帧之间的所有 IMU 测量数据进行积分得到，作为估计的初始值。这里的姿态/旋转采用四元数， $$ \begin{align*} p_{b_{k+1}}^w &= p_{b_k}^w + v_{b_k}^w \Delta t_k + \iint_{t\in[t_k, t_{k+1}]} (R_t^w (\hat a_t - b_{a_t} - n_a) - g^w) dt^2 \newline v_{b_{k+1}}^w &= v_{b_k}^w + \int_{t\in[t_k, t_{k+1}]} (R_t^w (\hat a_t - b_{a_t} - n_a) - g^w) dt \newline q_{b_{k+1}}^w &= q_{b_k}^w \otimes \int_{t\in[t_k, t_{k+1}]} \frac12 \Omega (\hat w_t - b_{w_t} - n_w) q_t^{b_k} dt \end{align*} \tag{1.3}\label{1.3} $$ 其中， $$ \Omega (w) = \begin{bmatrix} -\lfloor w \rfloor_\times & w \newline -w^T & 0 \end{bmatrix}, \ \ \lfloor w \rfloor_\times = \begin{bmatrix} 0 & -w_z & w_y \newline w_z & 0 & -w_x \newline -w_y & w_x & 0 \end{bmatrix} \tag{1.4} \label{1.4} $$

1.2.2 当前时刻在世界坐标系下离散形式 IMU 积分

公式 $\eqref{1.3}$ 是连续时刻的相机当前 PVQ 的迭代公式，为了结合器件采样与代码化，我们需要离散形式。为了与 VINS 保持一致，下面给出基于中值法的公式： $$ \begin{align*} p_{b_{i+1}}^w &= p_{b_i}^w + v_{b_i}^w \delta t + \frac12 \bar{\hat a}_i \delta t^2 \newline v _{b _{i+1}}^w &= v _{b_i}^w + \bar{\hat a}_i \delta t \newline q _{b _{i+1}}^w &= q _{b_i}^w \otimes \begin{bmatrix} 1 \newline \frac12 \bar{\hat w}_i \delta t \end{bmatrix} \end{align*} \tag{1.5} \label{1.5} $$ 其中， $$ \begin{align*} \bar{\hat a}_i &= \frac12 [ q_i (\hat a_i - b _{a_i}) - g^w + q _{i+1} (\hat a _{i_1} - b _{a_i}) - g^w ] \newline \bar{\hat w}_i &= \frac12 (\hat w_i + \hat w _{i+1}) - b _{w_i} \end{align*} \tag{1.6} \label{1.6} $$

1.2.3 两个兴趣帧之间基于前一帧坐标系下连续式 IMU 积分

可以看出，IMU状态传播需要帧 $b_k$ 的旋转、位置和速度。当这些起始状态发生变化时，我们需要重新积分 IMU 测量值。特别是在基于优化的算法中，每次调整姿势时，我们都需要在它们之间重新积分 IMU 测量值。这种积分策略在计算上要求很高。为了避免重复积分，VINS 参照采用了预积分算法。

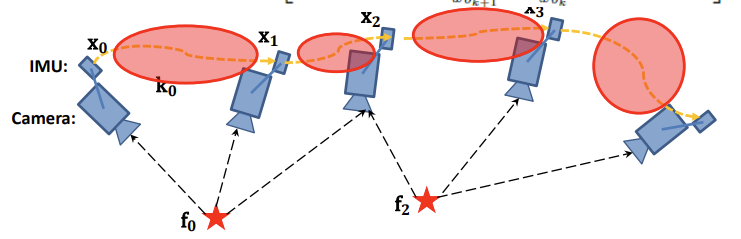
将参考坐标系从世界坐标系更改为局部坐标系 $b_k$ 后，可以仅预先积分与线性加速度 $\hat a$ 和角速度 $\hat w$ 有关，通过对公式 $\eqref{1.3}$ 等式左右两侧各乘以 $R_w^{b_k}$ ， $$ \begin{align*} R_w^{b_k} p_{b_{k+1}}^w &= R_w^{b_k} (p_{b_k}^w + v_{b_k}^w \Delta t_k - \frac12 g^w \Delta t_k^2) + \alpha_{b_{k+1}}^{b_k} \newline R_w^{b_k} v_{b_{k+1}}^w &= R_w^{b_k} (v_{b_k}^w - g^w \Delta t_k) + \beta_{b_{k+1}}^{b_k} \newline q_w^{b_k} \otimes q_{b_{k+1}}^w &= \gamma_{b_{k+1}}^{b_k} \end{align*} \tag{1.7} \label{1.7} $$

其中， $$ \begin{align*} \alpha_{b_{k+1}}^{b_k} &= \iint_{t \in [t_k, t_{k+1}]} R_t^{b_k} (\hat a_t - b_{a_t} - n_a) dt^2 \newline \beta_{b_{k+1}}^{b_k} &= \int_{t \in [t_k, t_{k+1}]} R_t^{b_k} (\hat a_t - b_{a_t} - n_a) dt \newline \gamma_{b_{k+1}}^{b_k} &= \int_{t \in [t_k, t_{k+1}]} \frac12 \Omega (\hat w - b_{w_t} - n_w) \gamma_t^{b_k} dt \end{align*} \tag{1.8} \label{1.8} $$ 式 $\eqref{1.8}$ 被称为预积分，可以仅通过 IMU 测量获取基于 $b_k$ 坐标系的积分传导。由此，$\alpha_{b_{k+1}}^{b_k},\ \beta_{b_{k+1}}^{b_k},\ \gamma_{b_{k+1}}^{b_k}$ 在 $b_k$ 与 $b_{k+1}$ 帧之间独立于其他状态量仅与 IMU 的 biases 有关。然而 bias 也是需要优化的变量，这将导致的问题是，每一次迭代更新得到一个新 bias 又需根据公式 $\eqref{1.8}$ 进行 $b_k$ 与 $b_{k+1}$ 帧之间的 IMU 预积分。当估计 bias 变化时候，如果 bias 变化很小，我可以通过泰勒展开一阶近似来模型化，这种策略为基于优化的算法节省了大量的计算资源，因为我们不需要重复积分传导 IMU 测量。假设预积分的变化量与 bias 是线性关系： $$ \begin{align*} \alpha_{b_{k+1}}^{b_k} &\approx \hat\alpha_{b_{k+1}}^{b_k} + J_{b_a}^\alpha \delta b_a + J_{b_w}^\alpha \delta b_w \newline \beta_{b_{k+1}}^{b_k} &\approx \hat\beta_{b_{k+1}}^{b_k} + J_{b_a}^\beta \delta b_a + J_{b_w}^\beta \delta b_w \newline \gamma_{b_{k+1}}^{b_k} &\approx \hat\gamma_{b_{k+1}}^{b_k} \otimes \begin{bmatrix} 1 \newline \frac12 J_{b_w}^\gamma b_w \end{bmatrix} \end{align*} \tag{1.9} \label{1.9} $$

1.2.4 两个兴趣帧之间基于前一帧坐标系下离散式 IMU 积分

对于离散时间的实现，可以应用不同的数值积分方法，例如欧拉、中值、RK4 积分。起始时刻 $\alpha_{b_k}^{b_k},\ \beta_{b_k}^{b_k}$ 为 0，而 $\gamma_{b_k}^{b_k}$ 为单位四元数。$\alpha, \ \beta, \ \gamma$ 的均值通过式 $\eqref{1.8}$ 进行迭代积分。请注意，加性噪声项 $n_a, \ n_w$ 是未知的，在执行实现中被视为零。这导致预积分项的估计值，用 $\hat{(\cdot)}$ 标记。论文中¹采用了欧拉积分进行推导，而代码中使用了中值积分。为了与代码中的公式一致，下面采用中值积分进行推导。 $$ \begin{align*} \hat\alpha _{i+1}^{b_k} &= \hat\alpha _i^{b_k} + \hat\beta _i^{b_k} \delta t + \frac12 \bar{\hat a}_i \delta t^2 \newline \hat\beta _{i+1}^{b_k} &= \hat\beta _{i}^{b_k} + \bar{\hat a}_i \delta t \newline \hat\gamma _{i+1}^{b_k} &= \hat\gamma _i^{b_k} \otimes \hat\gamma _{i+1}^i = \hat\gamma _i^{b_k} \otimes \begin{bmatrix} 1 \newline \frac12 \bar{\hat w}_i \delta t \end{bmatrix} \end{align*} \tag{1.10} \label{1.10} $$

其中， $$ \begin{align*} \bar{\hat a}_i &= \frac12 [q_i (\hat a_i - b _{a_i}) + q _{i+1} (\hat a _{i+1} - b _{a_i})] \newline \bar{\hat w}_i &= \frac12 (\hat w_i + \hat w _{i+1}) - b _{w_i} \end{align*} \tag{1.11} \label{1.11} $$

而 $i$ 是 IMU 在 $[t_k, t_{k+1}]$ 内测量采样对应的离散时刻，$\delta t$ 是两次 IMU 测量采样 $i$ 与 $i+1$ 之间的时间间隔。

1.3 IMU 预积分的误差状态

接下来需要处理协方差传播。由于四维旋转四元数 $\gamma_t^{b_k}$ 被过度参数化，将其误差项定义为围绕其均值的扰动： $$ \gamma_t^{b_k} \approx \hat \gamma_t^{b_k} \otimes \begin{bmatrix} 1 \newline \frac12 \delta \theta_t^{b_k} \end{bmatrix} \tag{1.12} \label{1.12} $$

1.3.1 两帧之间增量误差的连续式模型

我们可以推导出式 $\eqref{1.8}$ 的误差项的连续时间线性化动力学： $$ \begin{align*} \begin{bmatrix} \delta\dot\alpha_t^{b_k} \newline \delta\dot\beta_t^{b_k} \newline \delta\dot\theta_t^{b_k} \newline \delta\dot b_{a_t} \newline \delta\dot b_{w_t} \end{bmatrix} &= \begin{bmatrix} 0 & I & 0 & 0 & 0 \newline 0 & 0 & -R_t^{b_k} \lfloor \hat a_t - b_{a_t} \rfloor_\times & -R_t^{b_k} & 0 \newline 0 & 0 & - \lfloor \hat w - b_{w_t} \rfloor_\times & 0 & -I \newline 0 & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} \delta\alpha_t^{b_k} \newline \delta\beta_t^{b_k} \newline \delta\theta_t^{b_k} \newline \delta b_{a_t} \newline \delta b_{w_t} \end{bmatrix} \newline &+ \begin{bmatrix} 0 & 0 & 0 & 0 \newline -R_t^{b_k} & 0 & 0 & 0 \newline 0 & -I & 0 & 0 \newline 0 & 0 & I & 0 \newline 0 & 0 & 0 & I \end{bmatrix} \begin{bmatrix} n_a \newline n_w \newline n_{b_a} \newline n_{b_w} \end{bmatrix} = F_t \delta z_t^{b_k} + G_t n_t \end{align*} \tag{1.13} \label{1.13} $$

其中维度为 $F_t^{15 \times 15}, \ G_t^{15 \times 12}, \ \delta z_t^{b_k \ 15\times1}, \ n_t^{12 \times 1}$ 。依据式 $\eqref{1.2}$ 与式 $\eqref{1.8}$ 易得到 $\delta\dot b_{a_t},\ \delta\dot b_{w_t}$ 和 $\delta\dot\alpha_t^{b_k}$ 的如上等式，下面参照 《Quaternion kinematics for the error-state Kalman filter》³ 中 5.3 节针对 $\delta\dot\beta_t^{b_k}$ 和 $\delta\dot\theta_t^{b_k}$ 进行推导。

1.3.1a $\delta\dot\beta_t^{b_k}$ 项推导

$$ \begin{align*} \dot{\hat \beta}_t^{b_k} + \delta\dot\beta_t^{b_k} &= \dot\beta_t^{b_k} = \hat R_t^{b_k} exp(\lfloor \delta \theta_t^{b_k} \rfloor _\times)(\hat a_t - \hat b _{a_t} - \delta b _{a_t} - n_a) \newline \hat R_t^{b_k}(\hat a_t - \hat b _{a_t}) + \delta\dot\beta_t^{b_k} &= \quad \ \approx \hat R_t^{b_k} (I + \lfloor \delta \theta_t^{b_k} \rfloor _\times)(\hat a_t - \hat b _{a_t} - \delta b _{a_t} - n_a)\newline \delta\dot\beta_t^{b_k} &\approx \hat R_t^{b_k} (I + \lfloor \delta \theta_t^{b_k} \rfloor _\times)(\hat a_t - \hat b _{a_t} - \delta b _{a_t} - n_a) - \hat R_t^{b_k}(\hat a_t - \hat b _{a_t}) \newline \delta\dot\beta_t^{b_k} &\approx \hat R_t^{b_k} (\hat a_t - \hat b _{a_t}) - \hat R_t^{b_k} \delta b _{a_t} - \hat R_t^{b_k} n_a + \hat R_t^{b_k} \lfloor \delta \theta_t^{b_k} \rfloor _\times (\hat a_t - \hat b _{a_t}) \newline & \quad \ - \hat R_t^{b_k}(\hat a_t - \hat b _{a_t}) \newline &= - \hat R_t^{b_k} \lfloor \hat a_t - \hat b _{a_t} \rfloor _\times \delta \theta_t^{b_k} - \hat R_t^{b_k} \delta b _{a_t} - \hat R_t^{b_k} n_a \end{align*} \tag{1.14} \label{1.14} $$

1.3.1b $\delta\dot\theta_t^{b_k}$ 项推导

$$ \begin{align*} \underbrace{ \dot{(\hat\gamma_t^{b_k} \otimes \delta\gamma_t^{b_k})} } _{\enclose{roundedbox}{1}} &= \dot \gamma_t^{b_k} = \underbrace{ \frac12 \Omega(\hat w - \hat b _{w_t} - \delta b _{w_t} - n_w) (\hat\gamma_t^{b_k} \otimes \delta \gamma_t^{b_k}) } _{\enclose{roundedbox}{2}} \newline \enclose{roundedbox}{1} &= \dot{\hat \gamma}_t^{b_k} \otimes \delta\gamma_t^{b_k} + \hat \gamma_t^{b_k} \otimes \delta\dot\gamma_t^{b_k} \newline &= \frac12 \hat\gamma_t^{b_k} \otimes \begin{bmatrix} 0 \newline \hat w - \hat b _{w_t} \end{bmatrix} \otimes \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} + \hat \gamma_t^{b_k} \otimes \delta\dot\gamma_t^{b_k} \newline \enclose{roundedbox}{2} &= \frac12 \hat\gamma_t^{b_k} \otimes \delta\gamma_t^{b_k} \otimes \begin{bmatrix} 0 \newline \hat w - \hat b _{w_t} - \delta b _{w_t} - n_w \end{bmatrix} \newline &= \frac12 \hat\gamma_t^{b_k} \otimes \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \otimes \begin{bmatrix} 0 \newline \hat w - \hat b _{w_t} - \delta b _{w_t} - n_w \end{bmatrix} \newline \hat \gamma_t^{b_k} \otimes \delta\dot\gamma_t^{b_k} &= \frac12 \hat\gamma_t^{b_k} \otimes \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \otimes \begin{bmatrix} 0 \newline \hat w - \hat b _{w_t} - \delta b _{w_t} - n_w \end{bmatrix} \newline & \quad \ - \frac12 \hat\gamma_t^{b_k} \otimes \begin{bmatrix} 0 \newline \hat w - \hat b _{w_t} \end{bmatrix} \otimes \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \newline \text{令} \ \phi &= \hat w - \hat b _{w_t} - \delta b _{w_t} - n_w ,\ \psi = \hat w - \hat b _{w_t} \newline 2 \delta\dot\gamma_t^{b_k} &= \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \otimes \begin{bmatrix} 0 \newline \phi \end{bmatrix} - \begin{bmatrix} 0 \newline \psi \end{bmatrix} \otimes \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \newline \begin{bmatrix} 0 \newline \delta\dot\theta_t^{b_k} \end{bmatrix} &= \begin{bmatrix} 0 & -\phi^T \newline \phi & -\lfloor \phi \rfloor _\times \end{bmatrix} \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} - \begin{bmatrix} 0 & -\psi^T \newline \psi & \lfloor \psi \rfloor _\times \end{bmatrix} \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \newline \begin{bmatrix} 0 \newline \delta\dot\theta_t^{b_k} \end{bmatrix} &= \begin{bmatrix} 0 & -\phi^T + \psi^T \newline \phi - \psi & -\lfloor \phi \rfloor _\times - \lfloor \psi \rfloor _\times \end{bmatrix} \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \newline \begin{bmatrix} 0 \newline \delta\dot\theta_t^{b_k} \end{bmatrix} &= \begin{bmatrix} 0 & (\delta b _{w_t} + n_w)^T \newline -\delta b _{w_t} - n_w & -2\lfloor \hat w - \hat b _{w_t} \rfloor _\times + \lfloor \delta b _{w_t} + n_w \rfloor _\times \end{bmatrix} \begin{bmatrix} 1 \newline \frac12 \delta\theta_t^{b_k} \end{bmatrix} \newline \delta\dot\theta_t^{b_k} &\approx -\lfloor \hat w - \hat b _{w_t} \rfloor _\times \delta\theta_t^{b_k} -\delta b _{w_t} - n_w \end{align*} \tag{1.15} \label{1.15} $$

1.3.2 IMU 预积分误差连续形式下的协方差及雅克比

式 $\eqref{1.13}$ 可以被简写为 $\delta\dot z_t^{b_k} = F_t \delta z_t^{b_k} + G_t n_t$ ，根据导数定义可知： $$ \begin{align*} \delta\dot z_t^{b_k} &= \lim_{\delta t \to 0} \frac{\delta z_{t + \delta t}^{b_k} - \delta z_t^{b_k}}{\delta t} \newline \delta z_{t + \delta t}^{b_k} &\approx \delta z_t^{b_k} + \delta\dot z_t^{b_k} \delta t = (I + F_t \delta t) \delta z_t^{b_k} + (G_t \delta t) n_t \newline & \doteq F \delta z_t^{b_k} + V n_t \end{align*} \tag{1.16} \label{1.16} $$ 其中令 $F \doteq I+F_t \delta t, \ V \doteq G_t \delta t$ ，以简明下一小节中离散形式的分析，且与代码中的符号对应。对公式 $\eqref{1.16}$ 的 IMU 误差状态运动方程再进一步说明。该式和 EKF 对比可知，上式恰好给出了如 EKF 一般对非线性系统线性化的过程，这里的意义是表示下一个时刻的 IMU 测量误差与上一时刻的呈线性关系。因此，我们可以根据当前时刻的值预测处下一个时刻的均值与协方差，式 $\eqref{1.16}$ 给出的是对均值的预测，协方差预测公式如下（根据协方差的定义易得）： $$ P_{t + \delta t}^{b_k} = (I + F_t \delta t) P_t^{b_k} (I + F_t \delta t)^T + (G_t \delta t) Q (G_t \delta t)^T \tag{1.17} \label{1.17} $$ 上式给出的是协方差离散时间的一阶迭代公式，初始值 $P_{b_k}^{b_k} = 0$ 。其中 $Q$ 是以 $(\sigma_a^2, \sigma_w^2, \sigma_{b_a}^2, \sigma_{b_w}^2)$ 为值的噪声项对角协方差矩阵。

同理，关联 $\delta z_{b_{k+1}}^{b_k}$ 的雅克比 $J_{b_{k+1}}$ 可以通过 $\delta z_{b_{k}}^{b_k}$ 初始值为 $J_{b_k} = I$ 的雅克比进行一阶迭代得到： $$ J_{t + \delta t} = (I + F_t \delta t) J_t \tag{1.18} \label{1.18} $$

1.3.3 两帧之间增量误差的离散式模型

根据式 $\eqref{1.13}$ 和式 $\eqref{1.16}$ 我们可以推导出增量误差的离散式模型，为了与代码一致，采用中值积分方式，且矩阵形式修改了变量顺序。对比 integration_base.h 中 midPointIntegration 函数发现 $V$ 中与前四个噪声项相关系数相差一个负号，应该是推导过程与代码添加噪声的方式不同，即是减去一个噪声还是加上一个噪声，问题不是特别大。 $$ \begin{align*} \begin{bmatrix} \delta \alpha_{k+1} \newline \delta \theta_{k+1} \newline \delta \beta_{k+1} \newline \delta b_{a_{k+1}} \newline \delta b_{w_{k+1}} \end{bmatrix} &= \begin{bmatrix} I & f_{01} & I \delta t & f_{03} & f_{04} \newline 0 & f_{11} & 0 & 0 & -I \delta t \newline 0 & f_{21} & I & f_{23} & f_{24} \newline 0 & 0 & 0 & I & 0 \newline 0 & 0 & 0 & 0 & I \end{bmatrix} \begin{bmatrix} \delta \alpha_k \newline \delta \theta_k \newline \delta \beta_k \newline \delta b_{a_k} \newline \delta b_{w_k} \end{bmatrix} \newline & + \begin{bmatrix} v_{00} & v_{01} & v_{02} & v_{03} & 0 & 0 \newline 0 & -\frac12 I \delta t & 0 & -\frac12 I \delta t & 0 & 0 \newline -\frac12 R_k \delta t & v_{21} & -\frac12 R_{k+1} \delta t & v_{23} & 0 & 0 \newline 0 & 0 & 0 & 0 & I \delta t & 0 \newline 0 & 0 & 0 & 0 & 0 & I \delta t \end{bmatrix} \begin{bmatrix} n_{a_k} \newline n_{w_k} \newline n_{a_{k+1}} \newline n_{w_{k+1}} \newline n_{b_a} \newline n_{b_w} \end{bmatrix} \end{align*} \tag{1.19} \label{1.19} $$ 其中， $$ \begin{cases} f_{01} = \frac12 \delta t \cdot f_{21} \newline \quad \ = -\frac14 R_k \lfloor \hat a_k - b_{a_k} \rfloor_\times \delta t^2 - \frac14 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times ( I - \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \rfloor_\times \delta t ) \delta t^2 \newline \newline f_{03} = \frac12 \delta t \cdot f_{23} = -\frac14 (R_k + R_{k+1}) \delta t^2 \newline \newline f_{04} = \frac12 \delta t \cdot f_{24} = \frac14 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \delta t^3 \newline \newline f_{11} = I - \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \rfloor_\times \delta t \newline \newline f_{21} = -\frac12 R_k \lfloor \hat a_k - b_{a_k} \rfloor_\times \delta t - \frac12 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times ( I - \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \rfloor_\times \delta t ) \delta t \newline \newline f_{23} = -\frac12 (R_k + R_{k+1}) \delta t \newline \newline f_{24} = \frac12 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \delta t^2 \newline \newline v_{00} = -\frac14 R_k \delta t^2 \newline \newline v_{01} = v_{03} = \frac12 \delta t \cdot v_{21} = \frac14 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \delta t^2 \frac{\delta t}2 \newline \newline v_{02} = -\frac14 R_{k+1} \delta t^2 \newline \newline v_{21} = v_{23} = \frac14 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \delta t^2 \end{cases} \tag{1.19a} \label{1.19a} $$

1.3.3a $\delta \theta_{k+1}$ 项

根据式 $\eqref{1.16}$ 和式 $\eqref{1.15}$ ，利用中值积分有： $$ \begin{align*} \delta\theta_{k+1} &= \delta\theta_k + \delta\dot\theta_k \delta t \newline &= \delta\theta_k + \left( - \Big \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \Big \rfloor_\times \delta\theta_k - \frac12 (n_{w_k} + n_{w_{k+1}}) - \delta b_{w_k} \right) \delta t \newline &= \Big( I - \Big \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \Big \rfloor_\times \delta t \Big) \delta\theta_k - \frac12 \delta t (n_{w_k} + n_{w_{k+1}}) - \delta t \delta b_{w_k} \newline &= \Big( I - \Big \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \Big \rfloor_\times \delta t \Big) \delta\theta_k - \delta t \delta b_{w_k} - \frac12 \delta t n_{w_k} - \frac12 \delta t n_{w_{k+1}} \end{align*} \tag{1.20} \label{1.20} $$

1.3.3b $\delta\beta_{k+1}$ 项

根据式 $\eqref{1.16}$ 和式 $\eqref{1.14}$ ，利用中值积分有： $$ \begin{align*} \delta\beta_{k+1} &= \delta\beta_k + \delta\dot\beta_k \delta t \newline &= \delta\beta_k + \left( - \frac12 R_k \lfloor \hat a_k - b_{a_k} \rfloor_\times \delta\theta_k - \frac12 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \theta_{k+1} \right. \newline &\qquad \qquad \ \ \left. - \frac12 (R_k + R_{k+1}) \delta b_{a_k} - \frac12 R_k n_{a_k} - \frac12 R_{k+1} n_{a_{k+1}} \right) \delta t \newline &= \delta\beta_k + \left( - \frac12 R_k \lfloor \hat a_k - b_{a_k} \rfloor_\times \delta\theta_k - \frac12 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \right. \newline &\qquad \qquad \ \ \ \Big[ \Big( I - \Big \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \Big \rfloor_\times \delta t \Big) \delta\theta_k - \frac12 \delta t (n_{w_k} + n_{w_{k+1}}) - \delta t \delta b_{w_k} \Big] \newline &\qquad \qquad \ \ \left. - \frac12 (R_k + R_{k+1}) \delta b_{a_k} - \frac12 R_k n_{a_k} - \frac12 R_{k+1} n_{a_{k+1}} \right) \delta t \newline &= \left[ - \frac12 R_k \lfloor \hat a_k - b_{a_k} \rfloor_\times \delta t - \frac12 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \Big( I - \Big \lfloor \frac12 (\hat w_k + \hat w_{k+1}) - b_{w_k} \Big \rfloor_\times \delta t \Big) \delta t \right] \delta\theta_k \newline &\quad \ + \delta\beta_k - \frac12 (R_k + R_{k+1}) \delta t \delta b_{a_k} + \frac12 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \delta t^2 \delta b_{w_k} \newline &\quad \ -\frac12 R_k \delta t n_{a_k} + \frac14 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \delta t^2 n_{w_k} -\frac12 R_{k+1} \delta t n_{a_{k+1}} + \frac14 R_{k+1} \lfloor \hat a_{k+1} - b_{a_k} \rfloor_\times \delta t^2 n_{w_{k+1}} \end{align*} \tag{1.21} \label{1.21} $$

1.3.3c $\delta\alpha_{k+1}$ 项

根据式 $\eqref{1.16}$ 和式 $\eqref{1.19}$ ，利用中值积分有： $$ \begin{align*} \delta\alpha_{k+1} &= \delta\alpha_k + \delta\dot\alpha_k \delta t \newline &= \delta\alpha_k + \frac12 (\delta\beta_k + \delta\beta_{k+1}) \delta t \newline &= \delta\alpha_k + \frac12 \Big[\delta\beta_k + f_{21} \delta\theta_k + \delta\beta_k + f_{23} \delta b_{a_k} + f_{24} \delta b_{w_k} \newline &\qquad \qquad \quad \ -\frac12 R_k \delta t n_{a_k} + v_{21} n_{w_k} -\frac12 R_{k+1} \delta t n_{a_{k+1}} + v_{23} n_{w_{k+1}} \Big] \delta t \newline &= \delta\alpha_k + \frac12 \delta t \cdot f_{21} \delta\theta_k + \delta t \delta\beta_k -\frac14 (R_k + R_{k+1}) \delta t^2 \delta b_{a_k} + \frac12 \delta t \cdot f_{24} \delta b_{w_k} \newline & \ \ \ \ -\frac14 R_k \delta t^2 n_{a_k} + \frac12 \delta t \cdot v_{21} n_{w_k} - \frac14 R_{k+1} \delta t^2 n_{a_{k+1}} + \frac12 \delta t \cdot v_{23} n_{w_{k+1}} \end{align*} \tag{1.22} \label{1.22} $$

1.3.3d $\delta b_{a_k}$ 和 $\delta b_{w_k}$ 项

根据式 $\eqref{1.16}$ 和式 $\eqref{1.2}$ ，利用中值积分有： $$ \begin{align*} \delta b_{a_{k+1}} &= \delta b_{a_k} + \delta\dot b_{a_k} \delta t \newline &= \delta b_{a_k} + \delta t \cdot n_{b_a} \newline \newline \delta b_{w_{k+1}} &= \delta b_{w_k} + \delta\dot b_{w_k} \delta t \newline &= \delta b_{w_k} + \delta t \cdot n_{b_w} \end{align*} \tag{1.23} \label{1.23} $$

1.3.4 IMU 预积分误差离散形式下的雅克比、协方差与迭代更新

将式 $\eqref{1.19}$ 简写为： $$ \delta z_{k+1}^{15 \times 1} = F^{15 \times 15} \delta z_k^{15 \times 1} + V^{15 \times 18} Q^{18 \times 18} \tag{1.24} \label{1.24} $$ 则有雅克比的迭代公式为： $$ J_{k+1}^{15 \times 15} = F^{15 \times 15} J_k^{15 \times 15} \tag{1.25} \label{1.25} $$ 其中，雅克比的初始值为 $J_k = I$ 。这里计算出来的雅克比 $J_{k+1}$ 主要是为了后续迭代更新 IMU 预积分误差和求解残差时候提供对 bias 的雅克比。

协方差的迭代公式为： $$ P_{k+1}^{15 \times 15} = F^{15 \times 15} P_k^{15 \times 15}F^{T \ 15 \times 15} + V^{15 \times 18} Q^{18 \times 18} V^{T \ 18 \times 15} \tag{1.26} \label{1.26} $$ 其中，协方差的初始值 $P_k = 0$ 。其中 $Q$ 是以 $(\sigma_a^2, \sigma_w^2, \sigma_a^2, \sigma_w^2, \sigma_{b_a}^2, \sigma_{b_w}^2)$ 为值的噪声项对角协方差矩阵。

如前文介绍，当 bias 估计迭代更新有轻微变化时，将使用式 $\eqref{1.9}$ 的一阶近似对中值积分得到的预积分测量值进行矫正，而不重传播，从而得到更精确的预积分测量值。式 $\eqref{1.9}$ 中对应的几个雅克比是 $J_{k+1}$ 的一部分： $$ \begin{align*} J_{b_a}^\alpha &= \frac{\partial \delta\alpha_{b_{k+1}}^{b_k}}{\partial \delta b_{a_k}} = J_{k+1}(0:3, 9:12) \newline J_{b_w}^\alpha &= \frac{\partial \delta\alpha_{b_{k+1}}^{b_k}}{\partial \delta b_{w_k}} = J_{k+1}(0:3, 12:15) \newline J_{b_a}^\beta &= \frac{\partial \delta\beta_{b_{k+1}}^{b_k}}{\partial \delta b_{a_k}} = J_{k+1}(6:9, 9:12) \newline J_{b_w}^\beta &= \frac{\partial \delta\beta_{b_{k+1}}^{b_k}}{\partial \delta b_{w_k}} = J_{k+1}(6:9, 12:15) \newline J_{b_w}^\gamma &= \frac{\partial \delta\gamma_{b_{k+1}}^{b_k}}{\partial \delta b_{w_k}} = J_{k+1}(3:6, 12:15) \end{align*} \tag{1.27} \label{1.27} $$

2. IMU 残差及其雅克比

在 VINS 系统中的视觉重投影因子文章开头，介绍了 VINS 系统非线性求解 Bundle Adjustment 的结构，这里将不再重复。首先需要明确以下优化变量，一个 IMU 预积分因子关联的优化变量如下： $$ [p_{b_k}^w, q_{b_k}^w], \ [v_{b_k}^w, b_{a_k}, b_{w_k}], \ [p_{b_{k+1}}^w, q_{b_{k+1}}^w], \ [v_{b_{k+1}}^w, b_{a_{k+1}}, b_{w_{k+1}}] \tag{2.1} \label{2.1} $$

2.1 IMU 预积分残差

根据式 $\eqref{1.7}$下面将直接给出 IMU 预积分约束项，IMU 预积分残差（估计值 - 测量值）： $$ r_{\mathcal B} (\hat z_{b_{k+1}}^{b_k}, \mathcal{X})^{15 \times 1} = \begin{bmatrix} \delta\alpha_{b_{k+1}}^{b_k} \newline \delta\theta_{b_{k+1}}^{b_k} \newline \delta\beta_{b_{k+1}}^{b_k} \newline \delta b_a \newline \delta b_g \end{bmatrix} = \begin{bmatrix} R_w^{b_k} ( p_{b_{k+1}}^w - p_{b_k}^w - v_{b_k}^w \Delta t_k + \frac12 g^w \Delta t_k^2) - \alpha_{b_{k+1}}^{b_k} \newline 2 [{\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w]_{xyz} \newline R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k) - \beta _{b _{k+1}}^{b_k} \newline b _{a _{k _{k+1}}} - b _{a _{b_k}} \newline b _{w _{k _{k+1}}} - b _{w _{b_k}} \end{bmatrix} \tag{2.2} \label{2.2} $$

其中 $[\cdot]_{xyz}$ 表示提取四元数 $q$ 的向量部分以表示残差状态。$[\alpha _{b _{k+1}}^{b_k}, \beta _{b _{k+1}}^{b_k}, \gamma _{b _{k+1}}^{b_k}]^T$ 是 IMU 预积分测量项（式 $\eqref{1.9}$），仅在两个连续图像帧之间的时间间隔内使用噪声加速度计和陀螺仪测量，且利用线性化更新取消对 bias 更新后重复进行传播。加速度计和陀螺仪 biases 也包含在残差项中以进行在线校正。上式对应代码中 IntegrationBase::evaluate 函数。

2.2 IMU 预积分残差因子雅克比

计算 Jacobian 时，残差对应的求偏导对象为上面的优化变量，但是计算时采用扰动方式计算，即扰动为 $[\delta P_{b_k}^w, \delta \theta_{b_k}^w], \ [\delta v_{b_k}^w, \delta b_{a_k}, \delta b_{w_k}], \ [\delta p_{b_{k+1}}^w, \delta \theta_{b_{k+1}}^w], \ [\delta v_{b_{k+1}}^w, \delta b_{a_{k+1}}, \delta b_{w_{k+1}}]$ 。对于简单的线性项偏导将不再给出详细的推导过程，其中 PVQ 项关于 bias 的雅克比可以从式 $\eqref{1.27}$ 中获取。

2.2.1 对 $i$ 时刻 $[p_{b_k}^w, q_{b_k}^w]$ 求偏导

$$ J[0]^{15 \times 7} = \begin{bmatrix} \frac{\partial r_{\cal B}}{\partial p_{b_k}^w} & \frac{\partial r_{\cal B}}{\partial q_{b_k}^w} \end{bmatrix} = \begin{bmatrix} -R_w^{b_k} & \lfloor R_w^{b_k} (p_{b_{k+1}}^w - p_{b_k}^w - v_{b_k}^w \Delta t_k + \frac12 g^w \Delta t_k^2) \rfloor_\times \newline 0 & -\mathcal{L} [q_{b_{k+1}}^w {}^{-1} \otimes q_{b_k}^w] \mathcal{R}[\gamma_{b_{k+1}}^{b_k}] \newline 0 & \lfloor R_w^{b_k} (v_{b_{k+1}}^w - v_{b_k}^w + g^w \Delta t_k) \rfloor_\times \newline 0 & 0 \newline 0 & 0 \end{bmatrix} \tag{2.3} \label{2.3} $$

2.2.1a $\frac{\partial \delta\alpha_{b_{k+1}}^{b_k}}{\partial q_{b_k}^w}$ 项

$$ \begin{align*} \text{令}\ a &\doteq p_{b_{k+1}}^w - p_{b_k}^w - v_{b_k}^w \Delta t_k + \frac12 g^w \Delta t_k^2 \newline \frac{\partial \delta\alpha_{b_{k+1}}^{b_k}}{\partial q_{b_k}^w} &= \lim_{\delta\theta_{b_k}^w \to 0} \frac{ \exp(\lfloor \delta\theta_{b_k}^w \rfloor_\times)^T \hat R_w^{b_k} a - \hat R_w^{b_k} a}{\delta\theta_{b_k}^w} \newline &\approx \frac{ (I - \lfloor \delta\theta_{b_k}^w \rfloor_\times) \hat R_w^{b_k} a - \hat R_w^{b_k} a}{\delta\theta_{b_k}^w} \newline &= \frac{ \lfloor \hat R_w^{b_k} a \rfloor_\times \delta\theta_{b_k}^w}{\delta\theta_{b_k}^w} \newline &= \lfloor \hat R_w^{b_k} (p_{b_{k+1}}^w - p_{b_k}^w - v_{b_k}^w \Delta t_k + \frac12 g^w \Delta t_k^2) \rfloor_\times \end{align*} \tag{2.4} \label{2.4} $$

2.2.1b $\frac{\partial \delta\theta_{b_{k+1}}^{b_k}}{\partial q_{b_k}^w}$ 项

$$ \begin{align*} \frac{\partial \delta\theta_{b_{k+1}}^{b_k}}{\partial q_{b_k}^w} &= 2 \lim_{\delta\theta_{b_k}^w \to 0} \frac{{\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes \Bigg(\hat q_{b_k}^w \otimes \begin{bmatrix} 1 \newline \frac{\delta \theta_{b_k}^w}2 \end{bmatrix}\Bigg)^{-1} \otimes q_{b_{k+1}}^w - {\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes \Bigg(\hat q_{b_k}^w \otimes \begin{bmatrix} 1 \newline 0 \end{bmatrix}\Bigg)^{-1} \otimes q_{b_{k+1}}^w}{\delta\theta_{b_k}^w} \newline &= 2 \lim_{\delta\theta_{b_k}^w \to 0} \frac{{\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes \begin{bmatrix} 1 \newline -\frac{\delta \theta_{b_k}^w}2 \end{bmatrix} \otimes {\hat q_{b_k}^w }^{-1} \otimes q_{b_{k+1}}^w - {\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes \begin{bmatrix} 1 \newline 0 \end{bmatrix} \otimes {\hat q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w}{\delta\theta_{b_k}^w} \newline &= 2 \lim_{\delta\theta_{b_k}^w \to 0} \frac{\mathcal{R}[{\hat q_{b_k}^w }^{-1} \otimes q_{b_{k+1}}^w] \mathcal{L}[{\gamma_{b_{k+1}}^{b_k}}^{-1}] \Bigg( \begin{bmatrix} 1 \newline -\frac{\delta \theta_{b_k}^w}2 \end{bmatrix} - \begin{bmatrix} 1 \newline 0 \end{bmatrix} \Bigg)}{\delta\theta_{b_k}^w} \newline &= \lim_{\delta\theta_{b_k}^w \to 0} \frac{\mathcal{R}[{\hat q_{b_k}^w }^{-1} \otimes q_{b_{k+1}}^w] \mathcal{L}[{\gamma_{b_{k+1}}^{b_k}}^{-1}] \begin{bmatrix} 0 \newline -{\delta \theta_{b_k}^w} \end{bmatrix} }{\delta\theta_{b_k}^w} \newline &= \lim _{\delta\theta _{b_k}^w \to 0} \frac{- \Big[\mathcal{R}[{\hat q _{b_k}^w }^{-1} \otimes q _{b _{k+1}}^w] \mathcal{L}[{\gamma _{b _{k+1}}^{b_k}}^{-1}] \Big] _{3 \times 3} {\delta \theta _{b_k}^w} }{\delta\theta _{b_k}^w} \newline &\overset{\enclose{roundedbox}{1}}{=} \lim _{\delta\theta _{b_k}^w \to 0} \frac{- \Big[\mathcal{L}[{q _{b _{k+1}}^w}^{-1} \otimes \hat q _{b_k}^w] \mathcal{R}[\gamma _{b _{k+1}}^{b_k}] \Big] _{3 \times 3} {\delta \theta _{b_k}^w} }{\delta\theta _{b_k}^w} \newline &= - \Big[\mathcal{L}[{q _{b _{k+1}}^w}^{-1} \otimes \hat q _{b_k}^w] \mathcal{R}[\gamma _{b _{k+1}}^{b_k}] \Big] _{3 \times 3} \end{align*} \tag{2.5} \label{2.5} $$

其中 $\enclose{roundedbox}{1}$ 过程使用性质如下，令 $q = [s \ x \ y \ z]^T = [s \ w]^T$ ，则 $$ \begin{align*} \mathcal{R}[q] &= sI_{4 \times 4} + \Omega(w) = sI_{4 \times 4} + \begin{bmatrix} 0 & -w^T \newline w & -\lfloor w \rfloor_\times \end{bmatrix} \newline \mathcal{L}[q] &= sI_{4 \times 4} + \Psi(w) = sI_{4 \times 4} + \begin{bmatrix} 0 & -w^T \newline w & \lfloor w \rfloor_\times \end{bmatrix} \newline \text{则有：} & \mathcal{R}[q^{-1}] = sI_{4 \times 4} + \Omega(-w) = sI_{4 \times 4} + \begin{bmatrix} 0 & w^T \newline -w & \lfloor w \rfloor_\times \end{bmatrix} \newline \text{如果} & \text{只取右下角的 3x3 虚部部分，则有：} \newline \mathcal{R}[q^{-1}] _{3 \times 3} &= sI _{3 \times 3} + \lfloor w \rfloor _\times = \mathcal{L}[q] _{3 \times 3} \end{align*} \tag{2.5a} \label{2.5a} $$

2.2.1c $\frac{\partial \delta\beta_{b_{k+1}}^{b_k}}{\partial q_{b_k}^w}$ 项

$$ \begin{align*} \frac{\partial \delta\beta _{b _{k+1}}^{b_k}}{\partial q _{b_k}^w} &= \lim _{\delta\theta _{b_k}^w \to 0} \frac{\exp(\lfloor \delta\theta _{b_k}^w \rfloor _\times)^T \hat R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k) - \hat R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k)}{\delta\theta _{b_k}^w} \newline &\approx \lim _{\delta\theta _{b_k}^w \to 0} \frac{( I - \lfloor \delta\theta _{b_k}^w \rfloor _\times) \hat R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k) - \hat R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k)}{\delta\theta _{b_k}^w} \newline &= \lim _{\delta\theta _{b_k}^w \to 0} \frac{- \lfloor \delta\theta _{b_k}^w \rfloor _\times \hat R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k)}{\delta\theta _{b_k}^w} \newline &= \lim _{\delta\theta _{b_k}^w \to 0} \frac{\lfloor \hat R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k) \rfloor _\times \delta\theta _{b_k}^w}{\delta\theta _{b_k}^w} \newline &= \lfloor \hat R_w^{b_k} (v _{b _{k+1}}^w - v _{b_k}^w + g^w \Delta t_k) \rfloor _\times \end{align*} \tag{2.6} \label{2.6} $$

2.2.2 对 $i$ 时刻 $[v_{b_k}^w, b_{a_k}, b_{w_k}]$ 求偏导

$$ J[1]^{15 \times 9} = \begin{bmatrix} \frac{\partial r_{\cal B}}{\partial v_{b_k}^w} & \frac{\partial r_{\cal B}}{\partial b_{a_k}} & \frac{\partial r_{\cal B}}{\partial b_{w_k}} \end{bmatrix} = \begin{bmatrix} -R_w^{b_k} \Delta t & -J_{b_a}^\alpha & -J_{b_w}^\alpha \newline 0 & 0 & -\mathcal{L}[q_{b_{k+1}}^w{}^{-1} \otimes q_{b_k}^w \otimes \gamma_{b_{k+1}}^{b_k}] J_{b_w}^\gamma \newline -R_w^{b_k} & -J_{b_a}^\beta & -J_{b_w}^\beta \newline 0 & -I & 0 \newline 0 & 0 & -I \end{bmatrix} \tag{2.7} \label{2.7} $$

2.2.2a $\frac{\partial \delta\theta_{b_{k+1}}^{b_k}}{\partial b_{w_k}}$ 项

$$ \begin{align*} \frac{\partial \delta\theta_{b_{k+1}}^{b_k}}{\partial b_{w_k}} &= 2 \lim_{\delta b_{w_k} \to 0} \frac{ \Bigg[ {\hat \gamma_{b_{k+1}}^{b_k}} \otimes \begin{bmatrix} 1 \newline \frac12 J_{b_w}^\gamma \delta b_w \end{bmatrix} \Bigg]^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w - \Bigg[ {\hat \gamma_{b_{k+1}}^{b_k}} \otimes \begin{bmatrix} 1 \newline 0 \end{bmatrix} \Bigg]^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w }{\delta b_{w_k}} \newline &= 2 \lim_{\delta b_{w_k} \to 0} \frac{ \begin{bmatrix} 0 \newline -\frac12 J_{b_w}^\gamma \delta b_w \end{bmatrix} {\hat \gamma_{b_{k+1}}^{b_k}}^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w}{\delta b_{w_k}} \newline &= -\mathcal{R}[{\hat \gamma_{b_{k+1}}^{b_k}}^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w] \begin{bmatrix} 0 \newline J_{b_w}^\gamma \end{bmatrix} \newline &= -\mathcal{L}[{q _{b _{k+1}}^w}^{-1} \otimes q _{b_k}^w \otimes \hat \gamma _{b _{k+1}}^{b_k} ] _{3 \times 3} J _{b_w}^\gamma \end{align*} \tag{2.8} \label{2.8} $$

2.2.3 对 $j$ 时刻 $[p_{b_{k+1}}^w, q_{b_{k+1}}^w]$ 求偏导

$$ J[2]^{15 \times 7} = \begin{bmatrix} \frac{\partial r_{\cal B}}{\delta p_{b_{k+1}}^w} & \frac{\partial r_{\cal B}}{\partial q_{b_{k+1}}^w} \end{bmatrix} = \begin{bmatrix} R_w^{b_k} & 0 \newline 0 & \mathcal{L}[\gamma_{b_{k+1}}^{b_k}{}^{-1} \otimes q_{b_k}^w {}^{-1} \otimes q_{b_{k+1}}^w] \newline 0 & 0 \newline 0 & 0 \newline 0 & 0 \end{bmatrix} \tag{2.9} \label{2.9} $$

2.2.2a $\frac{\partial \delta\theta_{b_{k+1}}^{b_k}}{\partial q_{b_{k+1}}^w}$ 项

$$ \begin{align*} \frac{\partial \delta\theta_{b_{k+1}}^{b_k}}{\partial q_{b_{k+1}}^w} &= \lim_{\delta \theta_{b_{k+1}}^w \to 0} \frac{{\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w \otimes \begin{bmatrix} 1 \newline \frac12 \delta \theta_{b_{k+1}}^w \end{bmatrix} - {\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w \otimes \begin{bmatrix} 1 \newline 0 \end{bmatrix} }{\delta \theta_{b_k}^w} \newline &= \mathcal{L}[{\gamma_{b_{k+1}}^{b_k}}^{-1} \otimes {q_{b_k}^w}^{-1} \otimes q_{b_{k+1}}^w] \end{align*} \tag{2.10} \label{2.10} $$

2.2.4 对 $j$ 时刻 $[v_{b_{k+1}}^w, b_{a_{k+1}}, b_{w_{k+1}}]$ 求偏导

$$ J[3]^{15 \times 9} = \begin{bmatrix} \frac{\partial r_{\cal B}}{v_{b_{k+1}}^w} & \frac{\partial r_{\cal B}}{\partial b_{a_{k+1}}} & \frac{\partial r_{\cal B}}{\partial b_{w_{k+1}}} \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \newline 0 & 0 & 0 \newline R_w^{b_k} & 0 & 0 \newline 0 & I & 0 \newline 0 & 0 & I \end{bmatrix} \tag{2.11} \label{2.11} $$

2.3 小结

上面公式在代码中对应类：class IMUFactor : public ceres::SizedCostFunction<15, 7, 9, 7, 9> 。15 表示残差的维度。对于函数 Evaluate 输入参数 double const *const *parameters， 其中 parameters[0]、parameters[1]、parameters[2]、parameters[3] 分别对应 4 个输入参数, 它们的长度依次是 7,9,7,9 分别对应 4 个优化变量的参数块。

代码 IMUFactor::Evaluate() 函数中 residual 还乘以一个信息矩阵 sqrt_info,这是因为真正的优化项其实是 Mahalanobis 距离：$d = r^T P^{-1} r$ ，$P$ 是式 $\eqref{1.17}$ 中的协方差，又因为 Ceres 只接收最小二乘优化，也就是 $\min(e^T e)$ ，所以需要把 $P^{-1}$ 做 LLT 分解， 即 $LL^T = P^{-1}$ ，则有： $$ d = r^T L L^T r = (L^T r)^T (L^T r) \tag{2.12} \label{2.12} $$ 令 $r’ = L^T r$ 作为新的优化误差, 这样就能用 Ceres 求解了。Mahalanobis 距离其实相当于一个残差加权，协方差大的加权小，协方差小的加权大，着重优化那些比较确定的残差。

Reference