IMU Preintegration

0. 为什么需要 IMU 预积分

要解释 IMU 预积分的话，首先需要先了解正常情况下 IMU 积分与所谓的 IMU 预积分的区别。这里直接给出 IMU 积分过程（其中涉及到的 IMU 测量模型与运动学模型先不展开）。IMU 积分是指根据 IMU 传感器获取得到的加速度 $a_{t}$ 和角速度 $w_{t}$ ，与给定 IMU bias $b_{a_{t}}, b_{g_{t}}$ ，从第 $i$ 时刻的 $p_{b_{i}}^{w}, v_{b_{i}}^{w}, q_{b_{i}}^{w}$ 基础上不断积分得到第 $j$ 时刻的 $p_{b_{j}}^{w}, v_{b_{j}}^{w}, q_{b_{j}}^{w}$ 。如下图所示，

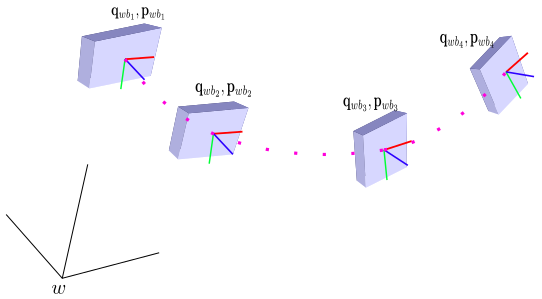
imu integration

IMU 积分公式如下： $\begin{matrix} (0.1) & \begin{aligned} p_{b_{j}}^{w} & = p_{b_{i}}^{w} + v_{i}^{w} Δ t_{k} + \iint_{t \in [i, j]} (q_{b_{t}}^{w} (a_{t} - b_{a_{t}} - n_{a}) - g^{w}) d t^{2} \\ v_{b_{j}}^{w} & = v_{b_{i}}^{w} + \int_{t \in [i, j]} (q_{b_{t}}^{w} (a_{t} - b_{a_{t}} - n_{a}) - g^{w}) d t \\ q_{b_{j}}^{w} & = \int_{t \in [i, j]} q_{b_{t}}^{w} \otimes [\begin{array}{c} 0 \\ \frac{1}{2} (w_{t} - b_{g_{t}} - n_{g}) \end{array}] d t \end{aligned} \end{matrix}$ 观察积分公式我们发现 $p_{b_{j}}^{w}, v_{b_{j}}^{w}, q_{b_{j}}^{w}$ 中的积分项依赖于初值 $p_{b_{i}}^{w}, v_{b_{i}}^{w}, q_{b_{i}}^{w}$ 。如果时刻 $b_{i}$ 的状态发生改变，时刻 $b_{j}$ 的状态必须重新计算。在基于优化的 Visual Inertial Odometry 算法中，状态每次迭代都会改变，如果每次迭代都重新积分，那么计算量会非常大。而预积分的目的就是想将这部分预先计算，且不受每次迭代更新重新计算，由此，我们需要想方法去掉基于 World 坐标系下的依赖项 $p_{b_{i}}^{w}, v_{b_{i}}^{w}, q_{b_{i}}^{w}$ 。

IMU 预积分技术最早由 T Lupton 于 12 年提出¹，以欧拉角为基础。C Forster 于 15 年²³⁴将其进一步拓展到李代数上，形成了一套优雅的理论体系。这套 IMU 预积分理论在开源因子图优化库 GTSAM 中进行实现，且被广泛应用于图优化框架的 VIO 中。其中包括 SVO2、ORB-SLAM3、VINS-Mono/Fusion、ICE-BA 等。由于这套理论的概念是在李群流行上的推导的，因此其中涉及到许多李群李代方面的知识，这部分知识可参考⁵⁶⁷（因此下文中使用到的一些公式、定义将直接给出，不再加以说明）。这套理论的后续发展有，Guoquan Huang 等⁸⁹¹⁰，在欧拉积分/二阶龙格库塔积分（Runge-Kutta 即，中值积分）基础上引入群空间闭式 (closed-form) 积分。

1. IMU 器件测量模型与运动学模型

IMU 通常包括一个三轴加速度计和一个三轴陀螺仪，能够测量传感器相对于惯性系的旋转速率和加速度。测量模型定义如下： $\begin{matrix} (1.1) & \begin{aligned} ^{b} \tilde{w} (t) & =^{b} w (t) + b_{g} (t) + η_{g} (t) \\ ^{b} \tilde{a} (t) & =_{b}^{w} R^{T} (^{w} a (t) -^{w} g) + b_{a} (t) + η_{a} (t) \end{aligned} \end{matrix}$ 其中 $^{b} \tilde{w} (t),^{b} \tilde{a} (t)$ 分别为陀螺仪与加速度计的测量值， $b$ 为随时间缓慢变化的 bias， $η$ 是白噪声。该模型利用了 Static World Assumption，由于 SLAM 的运行场景通常比较小（由此重力变化不大），且使用的 IMU 器件一般为 MEMS 器件（精度较低，陀螺仪静置时无法敏感到地球自转）。因此在上式 $(1.1)$ 测量模型中忽略了地球自转、重力矢量变化等影响因素，且假设运行区域水平面是一个平面。在此假设下的 VINS 中，世界坐标系 $w$ 被认为是一个惯性系，由此，下面的运动模型都是基于该假设进行推导。因此有运动模型的微分方程形式如下： $\begin{matrix} (1.2) & _{b}^{w} \dot{R} =_{b}^{w} R^{b} w^{\land},^{w} \dot{v} =^{w} a,^{w} \dot{p} =^{w} v \end{matrix}$ 根据上式， $t + Δ t$ 时刻的状态可以通过积分得： $\begin{matrix} (1.3) & \begin{aligned} _{b}^{w} R (t + Δ t) & =_{b}^{w} R (t) Exp (\int_{t}^{t + Δ t}^{b} w (τ) d τ) \\ ^{w} v (t + Δ t) & =^{w} v (t) + \int_{t}^{t + Δ t}^{w} a (τ) d τ \\ ^{w} p (t + Δ t) & =^{w} p (t) + \int_{t}^{t + Δ t}^{w} v (τ) d τ + \iint_{t}^{t + Δ t}^{w} a (τ) d τ \end{aligned} \end{matrix}$ 当假设在时间 $[t, t + Δ t]$ 内 $^{w} a$ 和 $^{b} w$ 是恒定的，使用欧拉积分，可以得到上式的离散形式如下： $\begin{matrix} (1.4) & \begin{aligned} _{b}^{w} R (t + Δ t) & =_{b}^{w} R (t) Exp (^{b} w (t) Δ t) \\ ^{w} v (t + Δ t) & =^{w} v (t) +^{w} a (t) Δ t \\ ^{w} p (t + Δ t) & =^{w} p (t) +^{w} v (t) Δ t + \frac{1}{2}^{w} a (t) Δ t^{2} \end{aligned} \end{matrix}$ 为了公式书写方便与符号简明，下面省略一些上下标记号，约定如下 $R ≐_{b}^{w} R, w ≐^{b} w, a ≐^{b} a, v ≐^{w} v, p ≐^{w} p, g ≐^{w} g$ 。将测量模型（式 $(1.1)$ ）带入离散运动模式（式 $(1.4)$ ）易得： $\begin{matrix} (1.5) & \begin{aligned} R (t + Δ t) & = R (t) Exp ((\tilde{w} (t) - b_{g} (t) - η_{g d} (t)) Δ t) \\ v (t + Δ t) & = v (t) + R (t) (\tilde{a} (t) - b_{a} (t) - η_{a d} (t)) Δ t + g Δ t \\ p (t + Δ t) & = p (t) + v (t) Δ t + \frac{1}{2} g Δ t^{2} + \frac{1}{2} R (t) (\tilde{a} (t) - b_{a} (t) - η_{a d} (t)) Δ t^{2} \end{aligned} \end{matrix}$ 上述公式中，我们注意到噪声采用的 $η_{g d}, η_{a d}$ ，其中下标 $d$ 表示为 discrete ，即使用了离散时间噪声，它们与连续噪声项 $η_{g}, η_{a}$ 是不同的，离散噪声与连续噪声的协方差有如下关系（Nikolas Trawny and Stergios I. Roumeliotis. Indirect Kalman Filter for 3D Attitude Estimation 2.1 有详细推导过程）： $\begin{matrix} (1.6) & \begin{aligned} Cov (η_{g d} (t)) & = \frac{1}{Δ t} Cov (η_{g} (t)) \\ Cov (η_{a d} (t)) & = \frac{1}{Δ t} Cov (η_{a} (t)) \end{aligned} \end{matrix}$

2. IMU 预积分

下面我们推导如何将两个关键帧 $k = i$ 和 $k = j$ 之间的所有 IMU 测量数据进行积分，由 $k = i$ 时刻的 $R_{i}, v_{i}, p_{i}$ 直接更新得到 $k = j$ 时刻的 $R_{j}, v_{j}, p_{j}$ 。过程如下图：

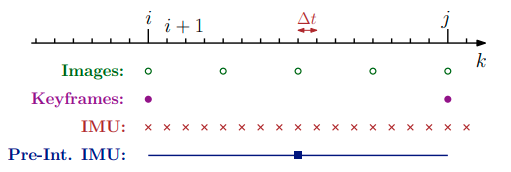
Different rates for IMU and camera

假设 IMU 的采样频率不变，即时间间隔 $Δ t$ 恒定，每个离散时刻由 $k = 0, 1, 2, \dots$ 表示，由此将式 $(1.5)$ 简化符号如下：

$\begin{matrix} (2.1) & \begin{aligned} R_{k + 1} & = R_{k} Exp (({\tilde{w}}_{k} - b_{g_{k}} - η_{{g d}_{k}}) Δ t) \\ v_{k + 1} & = v_{k} + R_{k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t + g Δ t \\ p_{k + 1} & = p_{k} + v_{k} Δ t + \frac{1}{2} g Δ t^{2} + \frac{1}{2} R_{k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t^{2} \end{aligned} \end{matrix}$

在关键帧 $k = i$ 和 $k = j$ 之间迭代所有 $Δ t$ 时间间隔的 IMU 积分有：

$\begin{matrix} (2.2) & \begin{aligned} R_{j} & = R_{i} \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - b_{g_{k}} - η_{{g d}_{k}}) Δ t) \\ v_{j} & = v_{i} + g Δ t_{i j} + \sum_{k = i}^{j - 1} R_{k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t \\ p_{j} & = p_{i} + \sum_{k = i}^{j - 1} v_{k} Δ t + \frac{j - i}{2} g Δ t^{2} + \frac{1}{2} \sum_{k = i}^{j - 1} R_{k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t^{2} \\ = p_{i} + \sum_{k = i}^{j - 1} (v_{k} Δ t + \frac{1}{2} g Δ t^{2} + \frac{1}{2} R_{k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t^{2}) \\ 其中, Δ t_{i j} & = \sum_{k = i}^{j - 1} Δ t = (j - i) Δ t \end{aligned} \end{matrix}$

为了避免每次更新初始的 $R_{i}$ ， $v_{i}$ 和 $p_{i}$ 都需要从头积分求解 $R_{j}$ ， $v_{j}$ 和 $p_{j}$ 。由此引出相对运动的预积分项（理想值）以避免依赖于 $R_{i}$ ， $v_{i}$ 和 $p_{i}$ ：

$\begin{matrix} (2.3) & \begin{aligned} Δ R_{i j} & ≐ R_{i}^{T} R_{j} = \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - b_{g_{k}} - η_{g d_{k}}) Δ t) \\ Δ v_{i j} & ≐ R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j}) = \sum_{k = i}^{j - 1} Δ R_{i k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t \\ Δ p_{i j} & ≐ R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) = \sum_{k = i}^{j - 1} [Δ v_{i k} Δ t + \frac{1}{2} Δ R_{i k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t^{2}] \\ 其中, Δ R_{i k} ≐ R_{i}^{T} R_{k}, Δ v_{i k} ≐ R_{i}^{T} (v_{k} - v_{i} - g Δ t_{i k}) \end{aligned} \end{matrix}$

需要注意的是虽然所称为 ‘‘delta’’ 量，但与 $Δ R_{i j}$ 相比， $Δ v_{i j}$ 和 $Δ p_{i j}$ 都不对应于速度和位置的真实物理变化，而是以一种使式 $(2.3)$ 的右侧独立于时刻 $i$ 的状态量和重力效应的方式定义的。使得我们能从两个关键帧之间的惯性测量直接计算式 $(2.3)$ 的右侧。上述三个预积分公式中，前两个式子的推导是显而易见的。而对于 $Δ p_{i j}$ 的推导如下（为了节省篇幅，令 $f_{k} = {\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}$ ），

$\begin{matrix} (2.3a) & \begin{aligned} p_{j} & - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2} \\ = \sum_{k = i}^{j - 1} (v_{k} Δ t + \frac{1}{2} g Δ t^{2} + \frac{1}{2} R_{k} f_{k} Δ t^{2}) - \sum_{k = i}^{j - 1} v_{i} Δ t - \frac{(j - i)^{2}}{2} g Δ t^{2} \\ = \sum_{k = i}^{j - 1} (v_{k} - v_{i}) Δ t + \underset{利用 \frac{j - i}{2} - \frac{(j - i)^{2}}{2} = - \frac{(j - i) [j - (i + 1)]}{2} = \sum_{k = i}^{j - 1} (k - i) 等差数列求和}{\underset{⏟}{[\frac{j - i}{2} - \frac{(j - i)^{2}}{2}]}} g Δ t^{2} + \frac{1}{2} \sum_{k = i}^{j - 1} R_{k} f_{k} Δ t^{2} \\ = \sum_{k = i}^{j - 1} (v_{k} - v_{i}) Δ t + \sum_{k = i}^{j - 1} (k - i) g Δ t^{2} + \frac{1}{2} \sum_{k = i}^{j - 1} R_{k} f_{k} Δ t^{2} \\ = \sum_{k = i}^{j - 1} {[v_{k} - v_{i} - (k - i) g Δ t] Δ t + \frac{1}{2} R_{k} f_{k} Δ t^{2}} \\ = \sum_{k = i}^{j - 1} [(v_{k} - v_{i} - g Δ t_{i k}) Δ t + \frac{1}{2} R_{k} f_{k} Δ t^{2}] \\ = \sum_{k = i}^{j - 1} (R_{i} Δ v_{i k} Δ t + \frac{1}{2} R_{k} f_{k} Δ t^{2}) \\ 等 & 式左右两边同时左乘 R_{i}^{T} \\ R_{i}^{T} & (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) \\ = \sum_{k = i}^{j - 1} (R_{i}^{T} R_{i} Δ v_{i k} Δ t + \frac{1}{2} R_{i}^{T} R_{k} f_{k} Δ t^{2}) = \sum_{k = i}^{j - 1} (Δ v_{i k} Δ t + \frac{1}{2} R_{i k} f_{k} Δ t^{2}) \\ = \sum_{k = i}^{j - 1} (Δ v_{i k} Δ t + \frac{1}{2} R_{i k} ({\tilde{a}}_{k} - b_{a_{k}} - η_{{a d}_{k}}) Δ t^{2}) \end{aligned} \end{matrix}$

我们注意到，即使采用式 $(2.3)$ 进行预积分计算，但是它依旧依赖于 bias 的估计。为了决绝这个问题，预积分算法将之分解与两个步骤：1. 首先假设两个关键帧之间的 bias 是一致的，即 $b_{g_{i}} = b_{g_{i + 1}} = \dots = b_{g_{j - 1}}, b_{a_{i}} = b_{a_{i + 1}} = \dots = b_{a_{j - 1}}$ 先进行预积分 IMU 测量值（[2.1 章节](#2.1 预积分 IMU 测量值)）；2. 当 bias 更新时，采用其他方式避免重复积分地更新预积分值（[2.3 章节](#2.3 伴随 bias 迭代更新的预积分测量更新)）。

2.1 预积分 IMU 测量值

式 $(2.3)$ 将关键帧 $i$ 和 $j$ 的状态（等式左侧）与测量值（等式右侧）联系起来。在这个意义上，可以被当初一个测量模型。不幸的是，它对测量噪声的依赖相当复杂，这使得 MAP 估计的直接应用也变得复杂。为了使得求解容易，需要将噪声项从惯性测量量中进行分离，使得预积分项变成 “ $测量值 = 理想值 \oplus 白噪声$ ” 的形式。

2.1.1 $Δ R_{i j}$ 项

$\begin{matrix} (2.4) & \begin{aligned} Δ R_{i j} & = \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - b_{g_{i}} - η_{g d_{k}}) Δ t) \\ 利用 Exp & (ϕ + δ ϕ) \approx Exp (ϕ) Exp (J_{r} (ϕ) δ ϕ), 且令 J_{r}^{k} ≐ J_{r} (({\tilde{w}}_{k} - b_{g_{i}}) Δ t) \\ ≃ \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - b_{g_{i}}) Δ t) Exp (- J_{r}^{k} η_{g d_{i}} Δ t) \\ 利用 Exp & (ϕ) R = R Exp (R^{T} ϕ) 将噪声项移至最后 \\ ≃ Δ {\tilde{R}}_{i j} \prod_{k = i}^{j - 1} Exp (- Δ {\tilde{R}}_{k + 1 j}^{T} J_{r}^{k} η_{g d_{k}} Δ t) \\ ≐ Δ {\tilde{R}}_{i j} Exp (- δ ϕ_{i j}) \end{aligned} \end{matrix}$

其中 $Δ {\tilde{R}}_{i j} ≐ \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - b_{g_{i}}) Δ t)$ 即为预积分旋转测量值，它由陀螺仪测量值和对陀螺仪 bias 的估计计算得到。而 $δ ϕ_{i j}$ 为其测量噪声。

2.1.2 $Δ v_{i j}$ 项

将式 $(2.4)$ ，即 $Δ R_{i j} ≐ Δ {\tilde{R}}_{i j} Exp (- δ ϕ_{i j})$ 代入 $Δ v_{i j}$ 的公式中，有

$\begin{matrix} (2.5) & \begin{aligned} Δ v_{i j} & = \sum_{k = i}^{j - 1} Δ R_{i k} ({\tilde{a}}_{k} - b_{a_{i}} - η_{{a d}_{k}}) Δ t \\ ≃ \sum_{k = i}^{j - 1} Δ {\tilde{R}}_{i k} Exp (- δ ϕ_{i k}) ({\tilde{a}}_{k} - b_{a_{i}} - η_{{a d}_{k}}) Δ t \\ 利用 \exp (δ ϕ^{\land}) \approx I + δ ϕ^{\land} & ≃ \sum_{k = i}^{j - 1} Δ {\tilde{R}}_{i k} (I - δ ϕ_{i k}^{\land}) ({\tilde{a}}_{k} - b_{a_{i}} - η_{{a d}_{k}}) Δ t \\ 忽略高阶小项 δ ϕ^{\land} η_{a d_{k}} & ≃ \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} (I - δ ϕ_{i k}^{\land}) ({\tilde{a}}_{k} - b_{a_{i}}) Δ t - Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t] \\ 利用 α^{\land} β = - β^{\land} α & ≃ \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}}) Δ t + Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t - Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t] \\ = \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}}) Δ t] + \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t - Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t] \\ ≐ Δ {\tilde{v}}_{i j} - δ v_{i j} \end{aligned} \end{matrix}$

其中 $Δ {\tilde{v}}_{i j} ≐ \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}}) Δ t]$ 即为预积分速度测量值，它由 IMU 测量值和对 bias 的估计计算得到。而 $δ v_{i j}$ 为其测量噪声。

2.1.3 $Δ p_{i j}$ 项

将式 $(2.4)$ 和式 $(2.5)$ ，即 $Δ R_{i j} ≐ Δ {\tilde{R}}_{i j} Exp (- δ ϕ_{i j})$ 和 $Δ v_{i j} ≐ Δ {\tilde{v}}_{i j} - δ v_{i j}$ 代入 $Δ p_{i j}$ 的公式中，有

$\begin{matrix} (2.6) & \begin{aligned} Δ p_{i j} & = \sum_{k = i}^{j - 1} [Δ v_{i k} Δ t + \frac{1}{2} Δ R_{i k} ({\tilde{a}}_{k} - b_{a_{i}} - η_{{a d}_{k}}) Δ t^{2}] \\ ≃ \sum_{k = i}^{j - 1} [(Δ {\tilde{v}}_{i k} - δ v_{i k}) Δ t + \frac{1}{2} Δ {\tilde{R}}_{i k} Exp (- δ ϕ_{i k}) ({\tilde{a}}_{k} - b_{a_{i}} - η_{{a d}_{k}}) Δ t^{2}] \\ 利用 \exp (δ ϕ^{\land}) \approx I + δ ϕ^{\land}, 且忽略高阶小项 δ ϕ^{\land} η_{a d_{k}} \\ ≃ \sum_{k = i}^{j - 1} [(Δ {\tilde{v}}_{i k} - δ v_{i k}) Δ t + \frac{1}{2} Δ {\tilde{R}}_{i k} (I - δ ϕ_{i k}^{\land}) ({\tilde{a}}_{k} - b_{a_{i}}) Δ t^{2} - \frac{1}{2} Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t^{2}] \\ 利用 α^{\land} β = - β^{\land} α \\ ≃ \sum_{k = i}^{j - 1} [Δ {\tilde{v}}_{i k} Δ t + \frac{1}{2} Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}}) Δ t^{2} \\ - δ v_{i k} Δ t + \frac{1}{2} Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t^{2} - \frac{1}{2} Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t^{2}] \\ ≐ Δ {\tilde{p}}_{i j} - δ p_{i j} \end{aligned} \end{matrix}$

其中 $Δ {\tilde{p}}_{i j} = \sum_{k = i}^{j - 1} [Δ {\tilde{v}}_{i k} Δ t + \frac{1}{2} Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}}) Δ t^{2}]$ 即为预积分位置测量值，它由 IMU 测量值和对 bias 的估计计算得到。而 $δ p_{i j}$ 为其测量噪声。

2.1.4 IMU 预积分测量模型

通过 2.1.1~2.1.3 我们有 $Δ R_{i j} ≐ Δ {\tilde{R}}_{i j} Exp (- δ ϕ_{i j})$ 、 $Δ v_{i j} ≐ Δ {\tilde{v}}_{i j} - δ v_{i j}$ 和 $Δ p_{i j} ≐ Δ {\tilde{p}}_{i j} - δ p_{i j}$ 将之代入式 $(2.3)$ 既能获取 IMU 预积分测量模型，即

$\begin{matrix} (2.7) & \begin{aligned} Δ {\tilde{R}}_{i j} & = Δ R_{i j} Exp (- δ ϕ_{i j})^{T} = R_{i}^{T} R_{j} Exp (δ ϕ_{i j}) \\ Δ {\tilde{v}}_{i j} & = Δ v_{i j} + δ v_{i j} = R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j}) + δ v_{i j} \\ Δ {\tilde{p}}_{i j} & = Δ p_{i j} + δ p_{i j} = R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) + δ p_{i j} \end{aligned} \end{matrix}$

2.2 预积分项的噪声传递

根据式 $(2.7)$ ，将 IMU 预积分测量模型的噪声定义为 $[δ ϕ_{i j}^{T}, δ v_{i j}^{T}, δ p_{i j}^{T}]^{T}$ 。通常我们将噪声向量近似为零均的正态分布，但是准确地建模噪声的协方差是至关重要的。由于在优化过程用的是马氏距离，需要用到协方差的逆对优化各项进行加权。由此需要对 IMU 预积分测量模型的噪声进行分析（目的是给出协方差的计算表达式）。假设 IMU 预积分测量模型的噪声满足如下：

$\begin{matrix} (2.8) & η_{i j}^{Δ} ≐ [δ ϕ_{i j}^{T} δ v_{i j}^{T} δ p_{i j}^{T}]^{T} \sim N (0_{9 \times 1}, Σ_{i j}) \end{matrix}$

为了证实该假设，首先我们来看 IMU 预积分测量旋转噪声 $δ ϕ_{i j}$ ，由式 $(2.4)$ 可得

$\begin{matrix} (2.9) & \begin{matrix} Exp (- δ ϕ_{i j}) = \prod_{k = i}^{j - 1} Exp (- Δ {\tilde{R}}_{k + 1 j}^{T} J_{r}^{k} η_{g d_{k}} Δ t) \\ 对两边去对数得 : δ ϕ_{i j} = - Log [\prod_{k = i}^{j - 1} Exp (- Δ {\tilde{R}}_{k + 1 j}^{T} J_{r}^{k} η_{g d_{k}} Δ t)] \\ 令 x_{k} = Δ {\tilde{R}}_{k + 1 j}^{T} J_{r}^{k} η_{g d_{k}} Δ t, 由于 η_{g d_{k}} 是小量, 于是有 J_{r} (x_{k}) \approx I, 则有 J_{r}^{- 1} (x_{k}) \approx I \\ \begin{aligned} δ ϕ_{i j} & = - Log [\prod_{k = i}^{j - 1} Exp (- x_{k})] = - Log [Exp (- x_{i}) \prod_{k = i + 1}^{j - 1} Exp (- x_{k})] \\ 利用 Log (Exp (ϕ) Exp (δ ϕ)) \approx ϕ + J_{r}^{- 1} δ ϕ \\ \approx - (- x_{i} + I Log [\prod_{k = i + 1}^{j - 1} Exp (- x_{k})]) \\ = x_{i} - Log [\prod_{k = i + 1}^{j - 1} Exp (- x_{k})] \\ = x_{i} - Log [Exp (- x_{i + 1}) \prod_{k = i + 2}^{j - 1} Exp (- x_{k})] \\ \approx x_{i} + x_{i + 1} - Log [\prod_{k = i + 2}^{j - 1} Exp (- x_{k})] \\ \approx x_{i} + x_{i + 1} + \dots + x_{j - 1} \\ = \sum_{k = i}^{j - 1} Δ {\tilde{R}}_{k + 1 j}^{T} J_{r}^{k} η_{g d_{k}} Δ t \end{aligned} \end{matrix} \end{matrix}$

由此易得 $δ ϕ_{i j}$ （一阶近似）满足零均高斯分布，因为它可以通过零均高斯噪声 $η_{g d_{k}}$ 的线性组合构成。

接下来我们来看 IMU 预积分测量速度噪声 $δ v_{i j}$ 和测量位置噪声 $δ p_{i j}$ ，由式 $(2.5)$ 和式 $(2.6)$ 易得：

$\begin{matrix} (2.10) & \begin{aligned} δ v_{i j} & = \sum_{k = i}^{j - 1} [- Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t + Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t] \\ δ p_{i j} & = \sum_{k = i}^{j - 1} [δ v_{i j} Δ t - \frac{1}{2} Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t^{2} + \frac{1}{2} Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t^{2}] \end{aligned} \end{matrix}$

通过上式易看出 $δ v_{i j}$ 和 $δ p_{i j}$ 由加速度噪声 $η_{a d_{k}}$ 和预积分测量旋转噪声 $δ ϕ_{i j}$ 线性组合而成，由于其两者都是零均的高斯噪声（ $δ ϕ_{i j}$ 在式 $(2.9)$ 已证明），所以 $δ v_{i j}$ 和 $δ p_{i j}$ 满足零均高斯分布。

通过式 $(2.9)$ 和式 $(2.10)$ 可知 IMU 预积分测量噪声 $η_{i j}^{Δ}$ 可由 IMU 测量噪声 $η_{k}^{d} ≐ [η_{g d_{k}}, η_{a d_{k}}], k = i, \dots, j - 1$ 线性组合构成。由于 IMU 测量噪声 $η_{k}^{d}$ 的协方差已知（可以通过标定或查阅数据手册），因此只需通过一系列线性组合就可以 IMU 预积分测量噪声 $η_{i j}^{Δ}$ 的协方差 $Σ_{i j}$ 了。为了满足实时性避免重复计算，下面推导预积分测量噪声协方差的递推形式。

2.2.1 $δ ϕ_{i j}$ 项的递推形式

根据式 $(2.9)$ 有

$\begin{matrix} (2.11) & \begin{aligned} δ ϕ_{i j} & ≃ \sum_{k = i}^{j - 1} Δ {\tilde{R}}_{k + 1 j}^{T} J_{r}^{k} η_{g d_{k}} Δ t \\ = \sum_{k = i}^{j - 2} Δ {\tilde{R}}_{k + 1 j}^{T} J_{r}^{k} η_{g d_{k}} Δ t + \overset{= I_{3 \times 3}}{\overset{⏞}{Δ {\tilde{R}}_{j j}^{T}}} J_{r}^{j - 1} η_{g d_{j - 1}} Δ t \\ = \sum_{k = i}^{j - 2} (\overset{Δ {\tilde{R}}_{k + 1 j}}{\overset{⏞}{Δ {\tilde{R}}_{k + 1 j - 1} Δ {\tilde{R}}_{j - 1 j}}})^{T} J_{r}^{k} η_{g d_{k}} Δ t + J_{r}^{j - 1} η_{g d_{j - 1}} Δ t \\ = Δ {\tilde{R}}_{j - 1 j}^{T} \sum_{k = i}^{j - 2} Δ {\tilde{R}}_{k + 1 j - 1}^{T} J_{r}^{k} η_{g d_{k}} Δ t + J_{r}^{j - 1} η_{g d_{j - 1}} Δ t \\ = Δ {\tilde{R}}_{j - 1 j}^{T} δ ϕ_{i j - 1} + J_{r}^{j - 1} η_{g d_{j - 1}} Δ t \end{aligned} \end{matrix}$

2.2.2 $δ v_{i j}$ 项的递推形式

根据式 $(2.10)$ 有

$\begin{matrix} (2.12) & \begin{aligned} δ v_{i j} & = \sum_{k = i}^{j - 1} [- Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t + Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t] \\ = \sum_{k = i}^{j - 2} [- Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t + Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t] \\ - Δ {\tilde{R}}_{i j - 1} ({\tilde{a}}_{j - 1} - b_{a_{i}})^{\land} δ ϕ_{i j - 1} Δ t + Δ {\tilde{R}}_{i j - 1} η_{a d_{j - 1}} Δ t \\ = δ v_{i j - 1} - Δ {\tilde{R}}_{i j - 1} ({\tilde{a}}_{j - 1} - b_{a_{i}})^{\land} δ ϕ_{i j - 1} Δ t + Δ {\tilde{R}}_{i j - 1} η_{a d_{j - 1}} Δ t \end{aligned} \end{matrix}$

2.2.3 $δ p_{i j}$ 项的递推形式

根据式 $(2.10)$ 有

$\begin{matrix} (2.13) & \begin{aligned} δ p_{i j} & = \sum_{k = i}^{j - 1} [δ v_{i j} Δ t - \frac{1}{2} Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t^{2} + \frac{1}{2} Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t^{2}] \\ = \sum_{k = i}^{j - 2} [δ v_{i j} Δ t - \frac{1}{2} Δ {\tilde{R}}_{i k} ({\tilde{a}}_{k} - b_{a_{i}})^{\land} δ ϕ_{i k} Δ t^{2} + \frac{1}{2} Δ {\tilde{R}}_{i k} η_{a d_{k}} Δ t^{2}] \\ + δ v_{i j - 1} Δ t - \frac{1}{2} Δ {\tilde{R}}_{i j - 1} ({\tilde{a}}_{j - 1} - b_{a_{i}})^{\land} δ ϕ_{i j - 1} Δ t^{2} + \frac{1}{2} Δ {\tilde{R}}_{i j - 1} η_{a d_{j - 1}} Δ t^{2} \\ = δ p_{i j - 1} + δ v_{i j - 1} Δ t - \frac{1}{2} Δ {\tilde{R}}_{i j - 1} ({\tilde{a}}_{j - 1} - b_{a_{i}})^{\land} δ ϕ_{i j - 1} Δ t^{2} + \frac{1}{2} Δ {\tilde{R}}_{i j - 1} η_{a d_{j - 1}} Δ t^{2} \end{aligned} \end{matrix}$

2.2.4 总结

整合式 $(2.11) (2.12) (2.13)$ ，可以得到 $η_{i j}^{Δ}$ 的递推形式如下：

$\begin{matrix} (2.14) & η_{i j}^{Δ} = \underset{A_{j - 1}}{\underset{⏟}{[\begin{matrix} Δ {\tilde{R}}_{j j - 1} & 0 & 0 \\ - Δ {\tilde{R}}_{i j - 1} ({\tilde{a}}_{j - 1} - b_{a_{i}})^{\land} Δ t & I & 0 \\ - \frac{1}{2} Δ {\tilde{R}}_{i j - 1} ({\tilde{a}}_{j - 1} - b_{a_{i}})^{\land} Δ t^{2} & Δ t I & I \end{matrix}]}} η_{i j - 1}^{Δ} + \underset{B_{j - 1}}{\underset{⏟}{[\begin{matrix} J_{r}^{j - 1} Δ t & 0 \\ 0 & Δ {\tilde{R}}_{i j - 1} Δ t \\ 0 & \frac{1}{2} Δ {\tilde{R}}_{i j - 1} Δ t^{2} \end{matrix}]}} η_{j - 1}^{d} \end{matrix}$

既有 $η_{i j}^{Δ} = A_{j - 1} η_{i j - 1}^{Δ} + B_{j - 1} η_{j - 1}^{d}$ ，由此根据协方差定义可得：

$\begin{matrix} (2.15) & Σ_{i j} = A_{j - 1} Σ_{i j - 1} A_{j - 1}^{T} + B_{j - 1} Σ_{η} B_{j - 1}^{T} \end{matrix}$

2.3 伴随 bias 迭代更新的预积分测量更新

在此之前的预积分都是假设了在两个关键帧 $k = i$ 和 $k = j$ 之间 IMU 的 bias ${{\bar{b}}_{a_{k}}, {\bar{b}}_{g_{k}}}$ 是恒定的基础上推导的。然而大多数情况下，IMU 的 bias 在优化过程中将伴随一个微小的增量 $δ b$ 进行变化。如果当 bias 变化时重新进行预积分 IMU 测量值，这将耗费巨大的计算量。因此，为了决绝这个问题，提出了利用线性化来进行 bias 变化时预积分测量项的一阶近似更新方式（ $\hat{b} \leftarrow \bar{b} + δ b$ ）：

$\begin{matrix} (2.16) & \begin{aligned} Δ {\tilde{R}}_{i j} ({\hat{b}}_{g_{i}}) & ≃ Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) Exp (\frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} δ b_{g_{i}}) \\ Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) & ≃ Δ {\tilde{v}}_{i j} ({\bar{b}}_{g_{i}}, {\bar{b}}_{a_{i}}) + \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{g}} δ b_{g_{i}} + \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{a}} δ b_{a_{i}} \\ Δ {\tilde{p}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) & ≃ Δ {\tilde{p}}_{i j} ({\bar{b}}_{g_{i}}, {\bar{b}}_{a_{i}}) + \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{g}} δ b_{g_{i}} + \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{a}} δ b_{a_{i}} \end{aligned} \end{matrix}$

其中 $\bar{b}$ 为旧 bias (原始假定) ， $\hat{b}$ 为新 bias (迭代更新所得) ，而 $δ b$ 是微小的增量。为了简化符号，假设已经在给定的偏差估计下的预积分变量为 $Δ {\bar{R}}_{i j} ≐ Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}), Δ {\bar{v}}_{i j} ≐ Δ {\tilde{v}}_{i j} ({\bar{b}}_{g_{i}}, {\bar{b}}_{a_{i}}), Δ {\bar{p}}_{i j} ≐ Δ {\tilde{p}}_{i j} ({\bar{b}}_{g_{i}}, {\bar{b}}_{a_{i}})$ 。为了执行 $(2.16)$ 的更新，需要计算其中的雅克比项。

2.3.1 $Δ {\tilde{R}}_{i j}$ 项关于 bias 的雅克比

根据式 $(2.4)$ 有：

$\begin{matrix} (2.17) & \begin{aligned} Δ {\tilde{R}}_{i j} ({\hat{b}}_{g_{i}}) & = \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - {\hat{b}}_{g_{i}}) Δ t) \\ = \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - ({\bar{b}}_{g_{i}} + δ b_{g_{i}})) Δ t) \\ = \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - {\bar{b}}_{g_{i}}) Δ t - δ b_{g_{i}} Δ t) \\ 利用 Exp & (ϕ + δ ϕ) \approx Exp (ϕ) Exp (J_{r} (ϕ) δ ϕ), 且令 {\bar{J}}_{r}^{k} ≐ J_{r} (({\tilde{w}}_{k} - {\bar{b}}_{g_{i}}) Δ t) \\ = \prod_{k = i}^{j - 1} Exp (({\tilde{w}}_{k} - {\bar{b}}_{g_{i}}) Δ t) Exp (- {\bar{J}}_{r}^{k} δ b_{g_{i}} Δ t) \\ 利用 Exp & (ϕ) R = R Exp (R^{T} ϕ) 将 δ b_{g_{i}} 噪声项移至最后 \\ = Δ {\bar{R}}_{i j} \prod_{k = i}^{j - 1} Exp (- Δ {\bar{R}}_{k + 1 j} {\bar{J}}_{r}^{k} δ b_{g_{i}} Δ t) \\ 利用 Log & (Exp (ϕ) Exp (δ ϕ)) \approx ϕ + J_{r} (ϕ)^{- 1} δ ϕ, 当 ϕ 也是小量时有 J_{r} (ϕ)^{- 1} \approx I \\ 由于 δ b_{g_{i}} & 为小量，因此 - Δ {\bar{R}}_{k + 1 j} {\bar{J}}_{r}^{k} δ b_{g_{i}} Δ t 也是小量, 令 α_{k} = - Δ {\bar{R}}_{k + 1 j} {\bar{J}}_{r}^{k} δ b_{g_{i}} Δ t \\ = Δ {\bar{R}}_{i j} Exp (α_{i}) Exp (α_{i + 1}) \prod_{k = i + 2}^{j - 1} Exp (α_{k}) \\ \approx Δ {\bar{R}}_{i j} Exp (α_{i} + α_{i + 1}) Exp (α_{i + 2}) Exp (α_{i + 3}) \prod_{k = i + 4}^{j - 1} Exp (α_{k}) \\ \approx Δ {\bar{R}}_{i j} Exp (\sum_{k = i}^{j - 1} α_{i}) \\ = Δ {\bar{R}}_{i j} Exp (\sum_{k = i}^{j - 1} (- Δ {\bar{R}}_{k + 1 j} {\bar{J}}_{r}^{k} δ b_{g_{i}} Δ t)) \end{aligned} \end{matrix}$

于是根据 $(2.16)$ 的定义有

$\begin{matrix} (2.18) & \frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} = \sum_{k = i}^{j - 1} (- Δ {\bar{R}}_{k + 1 j} {\bar{J}}_{r}^{k} Δ t), 其中 {\bar{J}}_{r}^{k} ≐ J_{r} (({\tilde{w}}_{k} - {\bar{b}}_{g_{i}}) Δ t) \end{matrix}$

2.3.2 $Δ {\tilde{v}}_{i j}$ 项关于 bias 的雅克比

根据式 $(2.5)$ 有：

$\begin{matrix} (2.19) & \begin{aligned} Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) & = \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} ({\hat{b}}_{g_{i}}) ({\tilde{a}}_{k} - {\hat{b}}_{a_{i}}) Δ t] \\ = \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} ({\hat{b}}_{g_{i}}) ({\tilde{a}}_{k} - ({\bar{b}}_{a_{i}} + δ b_{a_{i}})) Δ t] \\ 结合式 (2.16) (2.17) & = \sum_{k = i}^{j - 1} [Δ {\bar{R}}_{i k} Exp (\frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} δ b_{g_{i}}) ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}} - δ b_{a_{i}}) Δ t] \\ 利用 \exp (δ ϕ^{\land}) \approx I + δ ϕ^{\land} & \approx \sum_{k = i}^{j - 1} [Δ {\bar{R}}_{i k} (I + (\frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} δ b_{g_{i}})^{\land}) ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}} - δ b_{a_{i}}) Δ t] \\ 忽略高阶小项 & (\frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} δ b_{g_{i}})^{\land} δ b_{a_{i}}, 利用 α^{\land} β = - β^{\land} α, Δ {\bar{v}}_{i j} ≐ \sum_{k = i}^{j - 1} [Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}}) Δ t] \\ \approx Δ {\bar{v}}_{i j} - \sum_{k = i}^{j - 1} Δ {\bar{R}}_{i k} Δ t δ b_{a_{i}} + \sum_{k = i}^{j - 1} Δ {\bar{R}}_{i k} (\frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} δ b_{g_{i}})^{\land} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}}) Δ t \\ \approx Δ {\bar{v}}_{i j} - \sum_{k = i}^{j - 1} Δ {\bar{R}}_{i k} Δ t δ b_{a_{i}} - \sum_{k = i}^{j - 1} Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}})^{\land} \frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} Δ t δ b_{g_{i}} \end{aligned} \end{matrix}$

于是根据 $(2.16)$ 的定义有

$\begin{matrix} (2.20) & \begin{aligned} \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{g}} & = - \sum_{k = i}^{j - 1} Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}})^{\land} \frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} Δ t \\ \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{a}} & = - \sum_{k = i}^{j - 1} Δ {\bar{R}}_{i k} Δ t \end{aligned} \end{matrix}$

2.3.3 $Δ {\tilde{p}}_{i j}$ 项关于 bias 的雅克比

根据式 $(2.6)$ 有：

$\begin{matrix} (2.21) & \begin{aligned} Δ {\tilde{p}}_{i j} ({\hat{b}}_{g}, {\hat{b}}_{a}) & = \sum_{k = i}^{j - 1} [Δ {\tilde{v}}_{i k} ({\hat{b}}_{g}, {\hat{b}}_{a}) Δ t + \frac{1}{2} Δ {\tilde{R}}_{i k} ({\hat{b}}_{g_{i}}) ({\tilde{a}}_{k} - {\hat{b}}_{a_{i}}) Δ t^{2}] \\ = \underset{1}{\underset{⏟}{\sum_{k = i}^{j - 1} [Δ {\tilde{v}}_{i k} ({\hat{b}}_{g}, {\hat{b}}_{a}) Δ t]}} + \underset{2}{\underset{⏟}{\frac{1}{2} \sum_{k = i}^{j - 1} [Δ {\tilde{R}}_{i k} ({\hat{b}}_{g_{i}}) ({\tilde{a}}_{k} - {\hat{b}}_{a_{i}}) Δ t^{2}]}} \\ 1 & = \sum_{k = i}^{j - 1} [(Δ {\bar{v}}_{i k} + \frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{g}} δ b_{g_{i}} + \frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{a}} δ b_{a_{i}}) Δ t] \\ = \sum_{k = i}^{j - 1} [Δ {\bar{v}}_{i k} Δ t + \frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{g}} Δ t δ b_{g_{i}} + \frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{a}} Δ t δ b_{a_{i}}] \\ 2 & = \frac{1}{2} \sum_{k = i}^{j - 1} [Δ {\bar{R}}_{i k} Exp (\frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} δ b_{g_{i}}) ({\tilde{a}}_{k} - ({\bar{b}}_{a_{i}} + δ b_{a_{i}})) Δ t^{2}] \\ 忽略高阶小项 (\frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} δ b_{g_{i}})^{\land} δ b_{a_{i}}, 利用 \exp (δ ϕ^{\land}) \approx I + δ ϕ^{\land}, α^{\land} β = - β^{\land} α \\ \approx \frac{Δ t^{2}}{2} \sum_{k = i}^{j - 1} [Δ {\bar{R}}_{i k} (I + (\frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} δ b_{g_{i}})^{\land}) ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}} - δ b_{a_{i}})] \\ \approx \frac{Δ t^{2}}{2} \sum_{k = i}^{j - 1} [Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}}) - Δ {\bar{R}}_{i k} δ b_{a_{i}} - Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}})^{\land} \frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} δ b_{g_{i}}] \\ 1 + 2 & = \sum_{k = i}^{j - 1} [[Δ {\bar{v}}_{i k} Δ t + \frac{1}{2} Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}}) Δ t^{2}] + \\ [\frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{g}} Δ t - \frac{1}{2} Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}})^{\land} \frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} Δ t^{2}] δ b_{g_{i}} + \\ [\frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{a}} Δ t - \frac{1}{2} Δ {\bar{R}}_{i k} Δ t^{2}] δ b_{a_{i}}] \end{aligned} \end{matrix}$

于是根据 $(2.16)$ 的定义有

$\begin{matrix} (2.22) & \begin{aligned} Δ {\bar{p}}_{i j} & = \sum_{k = i}^{j - 1} [Δ {\bar{v}}_{i k} Δ t + \frac{1}{2} Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}}) Δ t^{2}] \\ \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{g}} & = \sum_{k = i}^{j - 1} [\frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{g}} Δ t - \frac{1}{2} Δ {\bar{R}}_{i k} ({\tilde{a}}_{k} - {\bar{b}}_{a_{i}})^{\land} \frac{\partial Δ {\bar{R}}_{i k}}{\partial b_{g}} Δ t^{2}] \\ \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{a}} & = \sum_{k = i}^{j - 1} [\frac{\partial Δ {\bar{v}}_{i k}}{\partial b_{a}} Δ t - \frac{1}{2} Δ {\bar{R}}_{i k} Δ t^{2}] \end{aligned} \end{matrix}$

通过 2.3.1~2.3.3 我们可知，当接收到新的测量数据时这些雅克比可以通过递增方式及时计算。

3. IMU 预积分残差

通过预积分测量模型 (式 $(2.7)$ ) 和测量噪声在一阶 (式 $(2.8)$ ) 上协方差为 $Σ_{i j}$ 的零均高斯噪声，因此可以得到关于 IMU 预积分因子的残差 $r_{I_{i j}} ≐ [r_{Δ R_{i j}}^{T}, r_{Δ v_{i j}}^{T}, r_{Δ p_{i j}}^{T}] \in R^{9}$ ，有：

$\begin{matrix} (3.1) & \begin{aligned} r_{Δ R_{i j}} & ≐ Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) Exp (\frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} δ b_{g_{i}}))^{T} R_{i}^{T} R_{j}) \\ r_{Δ v_{i j}} & ≐ R_{i} (v_{j} - v_{i} - g Δ t_{i j}) - [Δ {\tilde{v}}_{i j} ({\bar{b}}_{g_{i}}, {\bar{b}}_{a_{i}}) + \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{g}} δ b_{g_{i}} + \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{a}} δ b_{a_{i}}] \\ r_{Δ p_{i j}} & ≐ R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) - [Δ {\tilde{p}}_{i j} ({\bar{b}}_{g_{i}}, {\bar{b}}_{a_{i}}) + \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{g}} δ b_{g_{i}} + \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{a}} δ b_{a_{i}}] \end{aligned} \end{matrix}$

其中包含前面推导的伴随 bias 迭代更新的预积分测量如式 $(2.16)$ ，这种近似的修正方式避免了积分的重新计算，是预积分技术降低计算量的关键。

首先，需要先理解 IMU 预积分因子中的残差指的是预计预积分计算值 (由非 IMU 的其他方式估计的预积分值) 与 IMU 预积分测量值的差。在进行优化时，我们通常采用 “lift-solve-retract” 的方式，而每一次迭代过程将利用

$\begin{matrix} (3.2) & \begin{array}{rclcrcl} R_{i} & \leftarrow & R_{i} Exp (δ ϕ_{i}), & R_{j} & \leftarrow & R_{j} Exp (δ ϕ_{j}), \\ p_{i} & \leftarrow & p_{i} + R_{i} δ p_{i}, & p_{j} & \leftarrow & p_{j} + R_{j} δ p_{j}, \\ v_{i} & \leftarrow & v_{i} + δ v_{i}, & v_{j} & \leftarrow & v_{j} + δ v_{j}, \\ δ b_{g_{i}} & \leftarrow & δ b_{g_{i}} + \tilde{δ} b_{g_{i}}, & δ b_{a_{i}} & \leftarrow & δ b_{b_{i}} + \tilde{δ} b_{a_{i}} \end{array} \end{matrix}$

重新进行参数化式 $(3.1)$ ，通过增量来更新状态进而 retract 估计量，而 solve 步骤需要围绕当前估计的结果成本进行线性化，而线性化展开的目的是便于解析计算残差的雅克比行列表达式。这个过程通常被称之为 lifting ，它使得残差成为定义在易于计算雅克比行列式的向量空间上的函数。因此我们接下来将推导残差关于向量 $δ ϕ_{i}, δ p_{i}, δ v_{i}, δ ϕ_{j}, δ p_{j}, δ v_{j}, \tilde{δ} b_{g_{i}} \tilde{δ} b_{a_{i}}$ 的雅克比行列式。

3.1 残差 $r_{Δ R_{i j}}$ 的雅克比

由于 $r_{Δ R_{i j}}$ 中不含 $p_{i}, p_{j}, v_{i}, v_{j}, δ b_{a_{i}}$ ，因此 $r_{Δ R_{i j}}$ 关于这些状态增量的雅克比都为 0 。在 3.1.1~3.1.3 的推导中采用 $E ≐ Exp (\frac{\partial {\bar{R}}_{i j}}{\partial b_{g}} δ b_{g_{i}})$ 来进行速记。

3.1.1 残差 $r_{Δ R_{i j}}$ 关于 $δ ϕ_{i}$ 的雅克比

$\begin{matrix} (3.3) & \begin{aligned} r_{Δ R_{i j}} (R_{i} Exp (δ ϕ_{i})) & = Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E)^{T} (R_{i} Exp (δ ϕ_{i}))^{T} R_{j}) \\ = Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E)^{T} Exp (- δ ϕ_{i}) R_{i}^{T} R_{j}) \\ 利用 Exp (ϕ) R = R Exp (R^{T} ϕ) & = Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E)^{T} R_{i}^{T} R_{j} Exp (- R_{j}^{T} R_{i} δ ϕ_{i})) \\ = Log (Exp (Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E)^{T} R_{i}^{T} R_{j})) Exp (- R_{j}^{T} R_{i} δ ϕ_{i})) \\ 利用 & Log (Exp (ϕ) Exp (δ ϕ)) \approx ϕ + J_{r}^{- 1} (ϕ) δ ϕ \\ \approx r_{Δ R_{i j}} (R_{i}) - J_{r}^{- 1} (r_{Δ R_{i j}} (R_{i})) R_{j}^{T} R_{i} δ ϕ_{i} \end{aligned} \end{matrix}$

3.1.2 残差 $r_{Δ R_{i j}}$ 关于 $δ ϕ_{j}$ 的雅克比

$\begin{matrix} (3.4) & \begin{aligned} r_{Δ R_{i j}} (R_{j} Exp (δ ϕ_{j})) & = Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E)^{T} R_{i}^{T} R_{j} Exp (δ ϕ_{j})) \\ = Log (Exp (Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E)^{T} R_{i}^{T} R_{j})) Exp (δ ϕ_{j})) \\ 利用 & Log (Exp (ϕ) Exp (δ ϕ)) \approx ϕ + J_{r}^{- 1} (ϕ) δ ϕ \\ \approx r_{Δ R_{i j}} (R_{j}) + J_{r}^{- 1} (r_{Δ R_{i j}} (R_{j})) δ ϕ_{j} \end{aligned} \end{matrix}$

3.1.3 残差 $r_{Δ R_{i j}}$ 关于 $\tilde{δ} b_{g_{i}}$ 的雅克比

$\begin{matrix} (3.5) & \begin{aligned} r_{Δ R_{i j}} (δ b_{g_{i}} + \tilde{δ} b_{g_{i}}) & = Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) Exp (\frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} (δ b_{g_{i}} + \tilde{δ} b_{g_{i}})))^{T} R_{i}^{T} R_{j}) \\ 利用 & Exp (ϕ + δ ϕ) \approx Exp (ϕ) Exp (J_{r} (ϕ) δ ϕ), 令 J_{r}^{b} ≐ J_{r} (\frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} δ b_{g_{i}}) \\ = Log ((Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E Exp (J_{r}^{b} \frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} \tilde{δ} b_{g_{i}}))^{T} R_{i}^{T} R_{j}) \\ = Log (Exp (J_{r}^{b} \frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} \tilde{δ} b_{g_{i}})^{T} (Δ {\tilde{R}}_{i j} ({\bar{b}}_{g_{i}}) E)^{T} R_{i}^{T} R_{j}) \\ = Log (Exp (- J_{r}^{b} \frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} \tilde{δ} b_{g_{i}}) Exp (r_{Δ R_{i j}} (δ b_{g_{i}}))) \\ 利用 Exp (ϕ) R = R Exp (R^{T} ϕ) & = Log (Exp (r_{Δ R_{i j}} (δ b_{g_{i}})) \cdot \\ Exp (- Exp (r_{Δ R_{i j}} (δ b_{g_{i}}))^{T} J_{r}^{b} \frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} \tilde{δ} b_{g_{i}})) \\ 利用 & Log (Exp (ϕ) Exp (δ ϕ)) \approx ϕ + J_{r}^{- 1} (ϕ) δ ϕ \\ \approx r_{Δ R_{i j}} (δ b_{g_{i}}) - J_{r} (r_{Δ R_{i j}} (δ b_{g_{i}})) Exp (r_{Δ R_{i j}} (δ b_{g_{i}}))^{T} J_{r}^{b} \frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} \tilde{δ} b_{g_{i}} \end{aligned} \end{matrix}$

3.1.4 总结

根据上述的推导，残差 $r_{Δ R_{i j}}$ 关于 $δ ϕ_{i}, δ p_{i}, δ v_{i}, δ ϕ_{j}, δ p_{j}, δ v_{j}, \tilde{δ} b_{g_{i}} \tilde{δ} b_{a_{i}}$ 的雅克比为：

$\begin{matrix} (3.6) & \begin{aligned} \frac{\partial r_{Δ R_{i j}}}{\partial δ ϕ_{i}} & = - J_{r}^{- 1} (r_{Δ R_{i j}} (R_{i})) R_{j}^{T} R_{i} & \frac{\partial r_{Δ R_{i j}}}{\partial δ p_{i}} & = 0 \\ \frac{\partial r_{Δ R_{i j}}}{\partial δ v_{i}} & = 0 & \frac{\partial r_{Δ R_{i j}}}{\partial δ ϕ_{j}} & = J_{r}^{- 1} (r_{Δ R_{i j}} (R_{j})) \\ \frac{\partial r_{Δ R_{i j}}}{\partial δ p_{j}} & = 0 & \frac{\partial r_{Δ R_{i j}}}{\partial δ v_{j}} & = 0 \\ \frac{\partial r_{Δ R_{i j}}}{\partial \tilde{δ} b_{a_{i}}} & = 0 & \frac{\partial r_{Δ R_{i j}}}{\partial \tilde{δ} b_{g_{i}}} & = - J_{r} (r_{Δ R_{i j}} (δ b_{g_{i}})) Exp (r_{Δ R_{i j}} (δ b_{g_{i}}))^{T} J_{r}^{b} \frac{\partial Δ {\bar{R}}_{i j}}{\partial b_{g}} \end{aligned} \end{matrix}$

3.2 残差 $r_{Δ v_{i j}}$ 的雅克比

由于 $r_{Δ v_{i j}}$ 中不含 $R_{j}, p_{i}, p_{j}$ ，因此 $r_{Δ v_{i j}}$ 关于这些状态增量的雅克比都为 0 。

3.2.1 残差 $r_{Δ v_{i j}}$ 关于 $δ ϕ_{i}$ 的雅克比

$\begin{matrix} (3.7) & \begin{aligned} r_{Δ v_{i j}} (R_{i} Exp (ϕ_{i})) & = (R_{i} Exp (ϕ_{i}))^{T} (v_{j} - v_{i} - g Δ t_{i j}) - Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = Exp (ϕ_{i})^{T} R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j}) - Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = Exp (- ϕ_{i}) R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j}) - Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ 利用 Exp (δ ϕ) \approx I + δ ϕ^{\land} & \approx (I - δ ϕ_{i}^{\land}) R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j}) - Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = r_{Δ v_{i j}} (R_{i}) - δ ϕ_{i}^{\land} (R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j})) \\ 利用 α^{\land} β = - β^{\land} α & = r_{Δ v_{i j}} (R_{i}) + (R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j}))^{\land} δ ϕ_{i} \end{aligned} \end{matrix}$

3.2.3 残差 $r_{Δ v_{i j}}$ 关于 $δ v_{i}$ 和 $δ v_{j}$ 的雅克比

$\begin{matrix} (3.8) & \begin{aligned} r_{Δ v_{i j}} (v_{i} + δ v_{i}) & = R_{i}^{T} (v_{j} - v_{i} - δ v_{i} - g Δ t_{i j}) - Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = r_{Δ v_{i j}} (v_{i}) - R_{i}^{T} δ v_{i} \\ r_{Δ v_{i j}} (v_{j} + δ v_{j}) & = R_{i}^{T} (v_{j} + δ v_{j} - v_{i} - g Δ t_{i j}) - Δ {\tilde{v}}_{i j} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = r_{Δ v_{i j}} (v_{i}) + R_{i}^{T} δ v_{j} \end{aligned} \end{matrix}$

3.2.3 残差 $r_{Δ v_{i j}}$ 关于 $\tilde{δ} b_{a_{i}}$ 和 $\tilde{δ} b_{g_{i}}$ 的雅克比

由于 $r_{Δ v_{i j}}$ 关于 $δ b_{a_{i}}$ 和 $δ b_{g_{i}}$ 是线性的，因此 $r_{Δ v_{i j}}$ 关于 $\tilde{δ} b_{a_{i}}$ 和 $\tilde{δ} b_{g_{i}}$ 的雅克比可以直接依据线性系数得到，依赖于式 $(2.20)$ 易得：

$\begin{matrix} (3.9) & \begin{aligned} r_{Δ v_{i j}} (δ b_{a_{i}} + \tilde{δ} b_{a_{i}}) & = r_{Δ v_{i j}} (δ b_{a_{i}}) - \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{a}} \tilde{δ} b_{a_{i}} \\ r_{Δ v_{i j}} (δ b_{g_{i}} + \tilde{δ} b_{g_{i}}) & = r_{Δ v_{i j}} (δ b_{g_{i}}) - \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{g}} \tilde{δ} b_{g_{i}} \end{aligned} \end{matrix}$

3.2.4 总结

根据上述的推导，残差 $r_{Δ v_{i j}}$ 关于 $δ ϕ_{i}, δ p_{i}, δ v_{i}, δ ϕ_{j}, δ p_{j}, δ v_{j}, \tilde{δ} b_{g_{i}} \tilde{δ} b_{a_{i}}$ 的雅克比为：

$\begin{matrix} (3.10) & \begin{aligned} \frac{\partial r_{Δ v_{i j}}}{\partial δ ϕ_{i}} & = (R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j}))^{\land} & \frac{\partial r_{Δ v_{i j}}}{\partial δ p_{i}} & = 0 \\ \frac{\partial r_{Δ v_{i j}}}{\partial δ v_{i}} & = - R_{i}^{T} & \frac{\partial r_{Δ v_{i j}}}{\partial δ ϕ_{j}} & = 0 \\ \frac{\partial r_{Δ v_{i j}}}{\partial δ p_{j}} & = 0 & \frac{\partial r_{Δ v_{i j}}}{\partial δ v_{j}} & = R_{i}^{T} \\ \frac{\partial r_{Δ v_{i j}}}{\partial \tilde{δ} b_{a_{i}}} & = - \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{a}} & \frac{\partial r_{Δ v_{i j}}}{\partial \tilde{δ} b_{g_{i}}} & = - \frac{\partial Δ {\bar{v}}_{i j}}{\partial b_{g}} \end{aligned} \end{matrix}$

3.3 残差 $r_{Δ p_{i j}}$ 的雅克比

由于 $r_{Δ p_{i j}}$ 中不含 $R_{j}, v_{j}$ ，因此 $r_{Δ p_{i j}}$ 关于这些状态增量的雅克比都为 0 。

3.3.1 残差 $r_{Δ p_{i j}}$ 关于 $δ ϕ_{i}$ 的雅克比

$\begin{matrix} (3.11) & \begin{aligned} r_{Δ p_{i j}} (R_{i} Exp (δ ϕ_{i})) & = (R_{i} Exp (δ ϕ_{i}))^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) - Δ \tilde{p} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = Exp (δ ϕ_{i})^{T} R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) - Δ \tilde{p} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = Exp (- δ ϕ_{i}) R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) - Δ \tilde{p} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ 利用 Exp (δ ϕ) \approx I + δ ϕ^{\land} & \approx (I - δ ϕ_{i}^{\land}) (R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2})) - Δ \tilde{p} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = r_{Δ p_{i j}} (R_{i}) - δ ϕ_{i}^{\land} (R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2})) \\ 利用 α^{\land} β = - β^{\land} α & = r_{Δ p_{i j}} (R_{i}) - (R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}))^{\land} δ ϕ_{i} \end{aligned} \end{matrix}$

3.3.2 残差 $r_{Δ p_{i j}}$ 关于 $δ v_{i}$ 的雅克比

$\begin{matrix} (3.12) & \begin{aligned} r_{Δ p_{i j}} (v_{i} + δ v_{i}) & = R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - δ v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) - Δ \tilde{p} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = r_{Δ p_{i j}} (v_{i}) - R_{i}^{T} Δ t_{i j} δ v_{i} \end{aligned} \end{matrix}$

3.2.3 残差 $r_{Δ p_{i j}}$ 关于 $δ p_{i}$ 和 $δ p_{i}$ 的雅克比

$\begin{matrix} (3.13) & \begin{aligned} r_{Δ p_{i j}} (p_{i} + R_{i} δ p_{i}) & = R_{i}^{T} (p_{j} - p_{i} - R_{i} δ p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) - Δ \tilde{p} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = r_{Δ p_{i j}} (p_{i}) - I_{3 \times 3} δ p_{i} \\ r_{Δ p_{i j}} (p_{j} + R_{j} δ p_{j}) & = R_{i}^{T} (p_{j} + R_{j} δ p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}) - Δ \tilde{p} ({\hat{b}}_{g_{i}}, {\hat{b}}_{a_{i}}) \\ = r_{Δ p_{i j}} (p_{i}) + R_{i}^{T} R_{j} δ p_{i} \end{aligned} \end{matrix}$

3.3.4 残差 $r_{Δ p_{i j}}$ 关于 $\tilde{δ} b_{a_{i}}$ 和 $\tilde{δ} b_{g_{i}}$ 的雅克比

由于 $r_{Δ v_{i j}}$ 关于 $δ b_{a_{i}}$ 和 $δ b_{g_{i}}$ 是线性的，因此 $r_{Δ v_{i j}}$ 关于 $\tilde{δ} b_{a_{i}}$ 和 $\tilde{δ} b_{g_{i}}$ 的雅克比可以直接依据线性系数得到，依赖于式 $(2.22)$ 易得：

$\begin{matrix} (3.14) & \begin{aligned} r_{Δ p_{i j}} (δ b_{a_{i}} + \tilde{δ} b_{a_{i}}) & = r_{Δ p_{i j}} (δ b_{a_{i}}) - \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{a}} \tilde{δ} b_{a_{i}} \\ r_{Δ p_{i j}} (δ b_{g_{i}} + \tilde{δ} b_{g_{i}}) & = r_{Δ p_{i j}} (δ b_{g_{i}}) - \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{g}} \tilde{δ} b_{g_{i}} \end{aligned} \end{matrix}$

3.3.5 总结

根据上述的推导，残差 $r_{Δ p_{i j}}$ 关于 $δ ϕ_{i}, δ p_{i}, δ v_{i}, δ ϕ_{j}, δ p_{j}, δ v_{j}, \tilde{δ} b_{g_{i}} \tilde{δ} b_{a_{i}}$ 的雅克比为：

$\begin{matrix} (3.15) & \begin{aligned} \frac{\partial r_{Δ p_{i j}}}{\partial δ ϕ_{i}} & = (R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2}))^{\land} & \frac{\partial r_{Δ p_{i j}}}{\partial δ p_{i}} & = - I_{3 \times 3} \\ \frac{\partial r_{Δ p_{i j}}}{\partial δ v_{i}} & = - R_{i}^{T} Δ t_{i j} & \frac{\partial r_{Δ p_{i j}}}{\partial δ ϕ_{j}} & = 0 \\ \frac{\partial r_{Δ p_{i j}}}{\partial δ p_{j}} & = R_{i}^{T} R_{j} & \frac{\partial r_{Δ p_{i j}}}{\partial δ v_{j}} & = 0 \\ \frac{\partial r_{Δ p_{i j}}}{\partial \tilde{δ} b_{a_{i}}} & = - \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{a}} & \frac{\partial r_{Δ p_{i j}}}{\partial \tilde{δ} b_{g_{i}}} & = - \frac{\partial Δ {\bar{p}}_{i j}}{\partial b_{g}} \end{aligned} \end{matrix}$

4. Bias 模型

在介绍 IMU 模型时，式 $(1.1)$ ，我们说 biases 式随时间缓慢变化的量。因此，采用 “布朗运动 (Brownian motion)” 进行建模（补充：物理学中的布朗运动与数学中的 “维纳过程 (Wiener process)” 密切相关）。biases 白噪运动学的微分方程形式如下：

$\begin{matrix} (4.1) & {\dot{b}}_{g} (t) = η_{b_{g}}, {\dot{b}}_{a} (t) = η_{b_{a}} \end{matrix}$

根据上式，在两个连续关键帧 i 和 j 之间的时间间隔 $[t_{i}, t_{j}]$ 上积分得：

$\begin{matrix} (4.2) & b_{g_{j}} = b_{g_{i}} + η_{b_{g d}}, b_{a_{j}} = b_{a_{i}} + η_{b_{a d}} \end{matrix}$

其中，上式采用例如 $b_{g_{i}} ≐ b_{g} (t_{i})$ 进行速记，且定义带有零均值和协方差分别为 $Σ_{b_{g d}} ≐ Δ t_{i j} Cov (η_{b_{g}})$ 和 $Σ_{b_{a d}} ≐ Δ t_{i j} Cov (η_{b_{a}})$ 的离散噪声 $η_{b_{g d}}$ 和 $η_{b_{a d}}$ 。根据式 $(4.2)$ 可以简单被包含到因子图优化中，作为 IMU 预积分因子的附加项。

5. IMU 噪声的形式与单位

当我们在使用 IMU 的时候，离不开对 IMU Allan 方差的标定。这时候，我们通常会采用 kalibr_allan 或 allan_variance_ros 工具进行标定。根据式 $(1.6)$ 和第 4 节的内容，可知 IMU 的噪声形式分为连续形式和离散形式。而不同形式下其单位不同。结合前面的内容与对应的参考文献，下面直接给出不同形式下名称与单位。

名称	符号	单位
gyroscope white noise (or gyro noise density)	$σ_{g}$	$\frac{r a d}{s} \frac{1}{\sqrt{H z}}, = \frac{r a d}{\sqrt{s}}$
gyroscope random work (or gyro’s bias instability)	$σ_{b g}$	$\frac{r a d}{s^{2}} \frac{1}{\sqrt{H z}}, = \frac{r a d}{\sqrt{s^{3}}}$
accelerator white noise (or accel noise density)	$σ_{a}$	$\frac{m}{s^{2}} \frac{1}{\sqrt{H z}}$
accelerator random work (or accel’s bias instability)	$σ_{b a}$	$\frac{m}{s^{3}} \frac{1}{\sqrt{H z}}$
discrete gyroscope white noise	$σ_{g d}$	$\frac{r a d}{s}$
discrete gyroscope random work	$σ_{b g d}$	$\frac{r a d}{s}$
discrete accelerator white noise	$σ_{a d}$	$\frac{m}{s^{2}}$
discrete accelerator random work	$σ_{b a d}$	$\frac{m}{s^{2}}$

Reference

Todd Lupton and Salah Sukkarieh. Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions ; Manohar. Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions ↩︎
C Forster. On-Manifold Preintegration for Real-Time Visual-Inertial Odometry ↩︎
C Forster. IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation ↩︎
C Forster. Supplementary Material to: IMU Preintegration on Manifold for Ecient Visual-Inertial Maximum-a-Posteriori Estimation ↩︎
Timothy D. Barfoot. State Estimation For Robotics ↩︎
高翔. 视觉 SLAM 十四讲 ↩︎
邱笑晨. 预积分总结与公式推导 ↩︎
Kevin Eckenhoff, Patrick Geneva, and Guoquan Huang. Closed-form Preintegration Methods for Graph-based Visual-Inertial Navigation ↩︎
Kevin Eckenhoff, Patrick Geneva, and Guoquan Huang. Continuous Preintegration Theory for Graph-based Visual-Inertial Navigation ↩︎
Kevin Eckenhoff, Patrick Geneva, and Guoquan Huang. High-Accuracy Preintegration for Visual Inertial Navigation ↩︎

IMU Preintegration#

0. 为什么需要 IMU 预积分#

1. IMU 器件测量模型与运动学模型#

2. IMU 预积分#

2.1 预积分 IMU 测量值#

2.1.1 ΔRij 项#

2.1.2 Δvij 项#

2.1.3 Δpij 项#

2.1.4 IMU 预积分测量模型#

2.2 预积分项的噪声传递#

2.2.1 δϕij 项的递推形式#

2.2.2 δvij 项的递推形式#

2.2.3 δpij 项的递推形式#

2.2.4 总结#

2.3 伴随 bias 迭代更新的预积分测量更新#

2.3.1 ΔR~ij 项关于 bias 的雅克比#

2.3.2 Δv~ij 项关于 bias 的雅克比#

2.3.3 Δp~ij 项关于 bias 的雅克比#

3. IMU 预积分残差#

3.1 残差 rΔRij 的雅克比#

3.1.1 残差 rΔRij 关于 δϕi 的雅克比#

3.1.2 残差 rΔRij 关于 δϕj 的雅克比#

3.1.3 残差 rΔRij 关于 δ~bgi 的雅克比#

3.1.4 总结#

3.2 残差 rΔvij 的雅克比#

3.2.1 残差 rΔvij 关于 δϕi 的雅克比#

3.2.3 残差 rΔvij 关于 δvi 和 δvj 的雅克比#

3.2.3 残差 rΔvij 关于 δ~bai 和 δ~bgi 的雅克比#

3.2.4 总结#

3.3 残差 rΔpij 的雅克比#

3.3.1 残差 rΔpij 关于 δϕi 的雅克比#

3.3.2 残差 rΔpij 关于 δvi 的雅克比#

3.2.3 残差 rΔpij 关于 δpi 和 δpi 的雅克比#

3.3.4 残差 rΔpij 关于 δ~bai 和 δ~bgi 的雅克比#

3.3.5 总结#

4. Bias 模型#

5. IMU 噪声的形式与单位#

Reference#

IMU Preintegration

0. 为什么需要 IMU 预积分

1. IMU 器件测量模型与运动学模型

2. IMU 预积分

2.1 预积分 IMU 测量值

2.1.1 $Δ R_{i j}$ 项

2.1.2 $Δ v_{i j}$ 项

2.1.3 $Δ p_{i j}$ 项

2.1.4 IMU 预积分测量模型

2.2 预积分项的噪声传递

2.2.1 $δ ϕ_{i j}$ 项的递推形式

2.2.2 $δ v_{i j}$ 项的递推形式

2.2.3 $δ p_{i j}$ 项的递推形式

2.2.4 总结

2.3 伴随 bias 迭代更新的预积分测量更新

2.3.1 $Δ {\tilde{R}}_{i j}$ 项关于 bias 的雅克比

2.3.2 $Δ {\tilde{v}}_{i j}$ 项关于 bias 的雅克比

2.3.3 $Δ {\tilde{p}}_{i j}$ 项关于 bias 的雅克比

3. IMU 预积分残差

3.1 残差 $r_{Δ R_{i j}}$ 的雅克比

3.1.1 残差 $r_{Δ R_{i j}}$ 关于 $δ ϕ_{i}$ 的雅克比

3.1.2 残差 $r_{Δ R_{i j}}$ 关于 $δ ϕ_{j}$ 的雅克比

3.1.3 残差 $r_{Δ R_{i j}}$ 关于 $\tilde{δ} b_{g_{i}}$ 的雅克比

3.1.4 总结

3.2 残差 $r_{Δ v_{i j}}$ 的雅克比

3.2.1 残差 $r_{Δ v_{i j}}$ 关于 $δ ϕ_{i}$ 的雅克比

3.2.3 残差 $r_{Δ v_{i j}}$ 关于 $δ v_{i}$ 和 $δ v_{j}$ 的雅克比

3.2.3 残差 $r_{Δ v_{i j}}$ 关于 $\tilde{δ} b_{a_{i}}$ 和 $\tilde{δ} b_{g_{i}}$ 的雅克比

3.2.4 总结

3.3 残差 $r_{Δ p_{i j}}$ 的雅克比

3.3.1 残差 $r_{Δ p_{i j}}$ 关于 $δ ϕ_{i}$ 的雅克比

3.3.2 残差 $r_{Δ p_{i j}}$ 关于 $δ v_{i}$ 的雅克比

3.2.3 残差 $r_{Δ p_{i j}}$ 关于 $δ p_{i}$ 和 $δ p_{i}$ 的雅克比

3.3.4 残差 $r_{Δ p_{i j}}$ 关于 $\tilde{δ} b_{a_{i}}$ 和 $\tilde{δ} b_{g_{i}}$ 的雅克比

3.3.5 总结

4. Bias 模型

5. IMU 噪声的形式与单位

Reference