GVINS

Tightly Coupled GNSS-Visual-Inertial Fusion for Smooth and Consistent State Estimation¹ ( GNSS - 视觉 - 惯性紧耦合的状态估计器 ）该篇其实是作为 VINS-MONO² 一个方面拓展的非线性优化系统（因此与 VINS-MONO 相关重复的内容在这里略过，可以参考 VINS 系列）。主要是将 GNSS (Global Navigation Satellite System) 原始测量，结合视觉和惯性信息紧耦合以进行实时和无漂移的状态估计。我们知道视觉-惯导 (VIN) 系统有 4 个不可观的方向 : x, y, z, yaw 。因此作者引入 GNSS 系统为定位任务提供了无漂移和全局感知的解决方案。

1. 坐标系

由于引入了 GNSS 测量系统，因为会涉及到许多坐标系变化，因此需要先捋清坐标系间的变换关系。

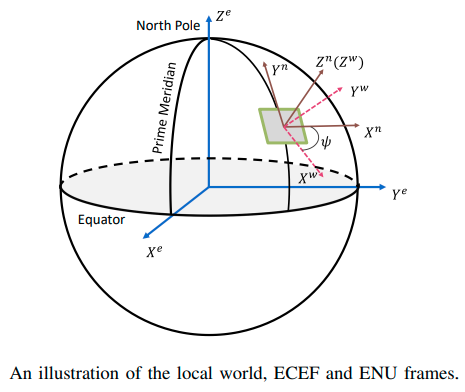
1. 传感器坐标系: 传感器坐标系连接到传感器，是传感器报告其读数的本地坐标系。在此系统中，传感器坐标系包括相机坐标系 $(\cdot)^c$ 和 IMU 坐标系 $(\cdot)^i$，该文章中选择 IMU 坐标系作为系统目标估计值，并表示为载体坐标系 $(\cdot)^b$ 。
2. 局部世界坐标系: 将传统的视觉惯性系统作为局部世界坐标系 $(\cdot)^w$ ，在 VIN 系统中，局部世界坐标系的原点是任意设置的，z 轴通常选择与局部地平面正交，如上图所示。
3. ECEF 坐标系: The Earth-Centered, Earth-Fixed （地心、地固）坐标系 $(\cdot)^e$ 是相对于地固定的笛卡尔坐标系，如上图所示。ECEF 坐标系的原点附着在质心上，z 轴垂直于地球的赤道，并指向真正的北方。x-y 平面与地球赤道重合，x 轴指向本初子午线。
4. ENU 坐标系: 为了连接局部世界坐标系和全局 ECEF 坐标系，引入了半全局坐标系， ENU 坐标系 $(\cdot)^n$ 。其 x、y、z 轴分别指向东、北、天(/上)方向（如上图所示）。给定 ECEF 坐标系中的一个点，可以确定一个独特的 ENU 坐标系，其原点位于该点上。需要注意的是，局部世界坐标系和 ENU 坐标系的 z 轴都平行于重力方向。
5. ECI 坐标系: The Earth-Centered Inertial （地心惯性）坐标系 $(\cdot)^E$ 是以地球质心为原点的惯性坐标系。ECI坐标系的三个轴相对于恒星指向固定的方向，即不随地球旋转。在 ECI 坐标系中，GNSS 信号以直线传播，大大简化了公式。在本文中，ECI 坐标系是通过在接收 GNSS 信号时冻结 ECEF 坐标系形成的。

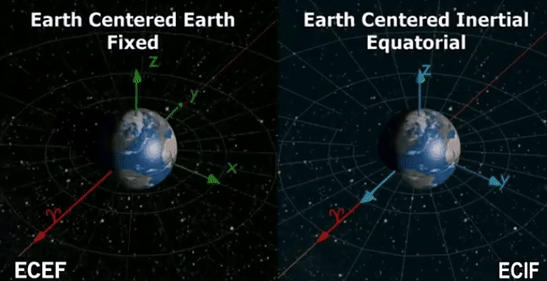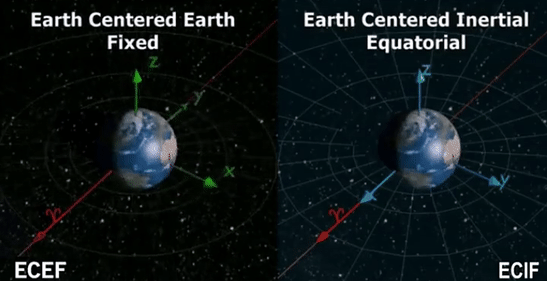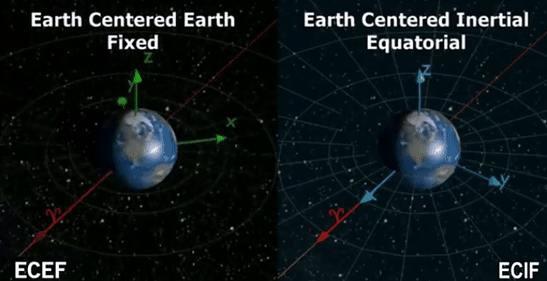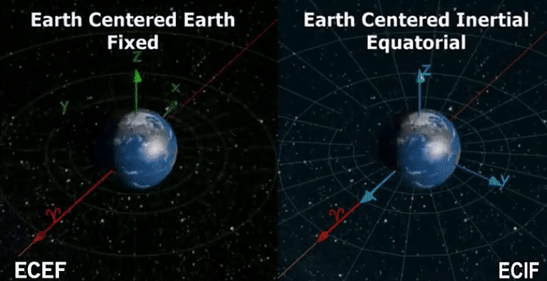
为了更好的说明 ECEF 坐标系与 ECI 坐标系的区别，引入上面动图来更加直观说明。除此了上文提及的坐标系，有些其他的 paper 或许会提及到 WGS-84 坐标（本论文中就是采用 WGS-84 来实现 [/转换成] ECEF 坐标系）。

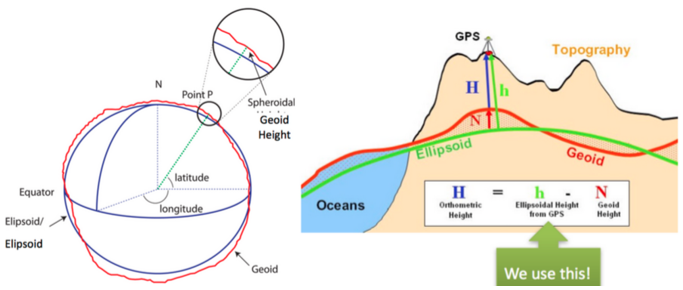
• WGS-84 坐标系: 可以说是最为广泛应用的一个地球坐标系，它给出一点的大地纬度、大地经度和大地高程而更加直观地告诉我们该点在地球中的位置，故又被称为经纬高坐标系（经度[longitude]、纬度[latitude]、高度[altitude] – LLA 坐标系，如下图表示）

  

  参数	WGS-84 值
  基准椭圆体的长半径 $a$	$6378137$ m
  基准椭圆体的短半径 $b$	$6356752.3142$ m
  扁率 $f$	$1/298.257223563$
  偏心率 $e$	$0.0818191908425$ m
  光速 $c$	$2.99792458*1e8$ m/s

  • LLA 与 ECEF 坐标系、ECEF 与 ENU 坐标系之间的互相转换算法可以参考 Geographic coordinate conversion

2. GNSS 基本原理

由于使用到了 GNSS 原始测量处理，因此需要对 GNSS 的背景知识有点了解。下面仅给出算法中用到的伪距 (Code Pseudorange Measurement) 和 多普勒频移 ( Doppler Measuremen) 测量建模进行介绍。而关于 GNSS 定位算法（伪距单点定位 SPP，精度 5-10 米；精密单点定位 PPP，可达厘米级；伪距双差定位 RTD，分米级，需要基站；载波双差定位 RTK，厘米级，需要基站；PPP-RTK，厘米级，需要区域性 CORS 站）更详细的知识请阅读原文亦或是阅读相关文档。

全球导航卫星系统（GNSS），顾名思义，是一种基于卫星的系统，能够提供全球定位服务。目前有四个独立且全面运行的系统，即 GPS、GLONASS、伽利略和北斗。每个 GNSS 系统由控制段、卫星段和用户段组成，用户段由无限数量的接收机组成。

卫星段是在约 20,000 公里高度绕地球轨道运行的卫星星座（北斗的 GSO/IGSO 卫星除外），其状态由控制段监测和更新。导航卫星不断发射特定的无线电信号，接收器可以从中唯一地识别卫星并检索导航信息。 GPS L1 信号的典型结构如下图所示。每颗卫星都有一个唯一的伪随机数 (PRN) 码，每 1 毫秒重复一次。包含卫星轨道和 GNSS 时间参数的导航电文（星历）首先与 PRN 码组合，然后用于调制高频载波信号。接收器接收到信号后，通过测量接收信号和设计信号之间的频率差来获得多普勒频移。伪距测量是从表示传播时间的 PRN 码位移推断出来的。最后，通过反向解调过程发现导航消息。

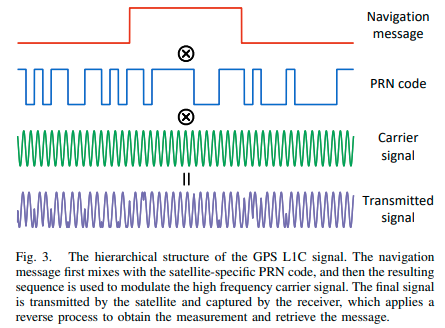
2.1 伪距测量

接收到信号后，信号的飞行时间 (ToF) 是根据 PRN 码移位来测量的。通过乘以光速，接收机获得伪距测量。伪距之所以称为“伪”，是因为它不仅包含卫星与接收机之间的几何距离，还包括信号产生、传播和处理过程中的各种误差。卫星侧误差源主要包括卫星轨道误差和时钟误差。轨道误差来自其他天体的影响，这些天体不是由星历精确建模的，时钟误差是卫星星载原子钟相对于标准系统时间不完善的结果。轨道和时钟误差由系统控制部分监控并不断纠正。 信号从卫星到接收器的传播过程中，经过电离层和对流层，电磁信号的速度不再与真空中的速度相同，并且信号根据大气成分和传播路径而延迟。信号以不同方式到达接收器的现象称为多径效应，可能会发生并增加额外的延迟，特别是对于低仰角卫星。当信号到达时，ToF 是通过将信号传输时间（由卫星的原子钟标记）与接收器不太准确的本地时钟时间进行比较来计算的。因此，距离信息也受影响于接收器时钟偏差相对于 GNSS 系统时间偏移。总之，伪距测量可以建模为： $$ \tilde{P}^s_r = \left | p^E_s - p^E_r\right | +c(\zeta^T_s \delta t - \Delta t^s) + T^s_r + I^s_r + M^s_r + \epsilon^s_r \tag{2.1} \label{2.1} $$ 其中， $p^E_s$ 和 $p^E_r$ 分别是卫星 s 和接收机 r 在 ECI 坐标系下的坐标值。$c$ 为真空中的光速。 $\zeta_s$ 是一个 $4 \times 1$ 的指标向量，对应的卫星星座实体为 1，其他三个实体为 0 。$\delta t$ 为接收机时钟偏差。 $\Delta t^s$ 为卫星时钟误差，由星历表计算得到。$T^s_r$ 和 $I^s_r$ 分别表示对流层延迟和电离层延迟补偿。$M^s_r$ 表示由多径效应引起的时延，$\epsilon^s_r$ 表示为测量噪声。

2.2 多普勒频移

多普勒频移是由接收到的载波信号与设计载波信号的差值来测量的，反映了接收机-卫星在信号传播路径上的相对运动。由于 GNSS 信号结构的特点，多普勒测量精度通常比伪距测量精度高一个数量级。多普勒频移模型为: $$ \Delta \tilde{f}^s_r = -\frac{1}{\lambda} \left [ \kappa^{sT}_r (\mathrm{v}^E_s - \mathrm{v}^E_r) + c(\dot{\delta t} - \dot{\Delta t^s}) \right ] + \eta^s_r \tag{2.2} \label{2.2} $$ 其中，$\mathrm{v^E_r}$ 和 $\mathrm{v}^E_s$ 分表表示接收机 r 和卫星 s 在 ECI 坐标系下的速度。$\lambda$ 表示载波信号的波长，$\kappa^s_r$ 表示在 ECI 坐标系下接收机到卫星的单位方向向量： $$ \kappa^s_r = \frac{p_s^E - p_r^E}{\lVert p_s^E - p_r^E \rVert} = \frac{p_s^E - p_r^E}{\sqrt{(p_s^E - p_r^E)^2}} \tag{2.3}\label{2.3} $$ 而 $\dot{\Delta t^s}$ 为星历表中卫星时钟误差的漂移率，$\dot{\delta t}$ 为接收机时钟偏差的漂移速率，$\eta^s_r$ 为多普勒测量噪声。

2.3 伪距单点定位

单点定位 (Single Point Positioning, SPP) 算法利用码伪距测量，通过三次迭代确定 GNSS 接收机的三自由度全球位置。因此，理论上可以通过 3 颗不同的卫星得到接收机的坐标。然而，正如在 2.1 节中提到的，码伪距测量被接收机时钟偏差所抵消。由于接收机的时钟偏差可能会造成数百公里的误差，因此必须将其连同位置一起估计，以便得到一个合理的结果。为此，至少需要 4 个码伪距测量来完全约束 3-DOF 全球位置和接收机时钟偏差。由于不同的导航系统使用不同的时间参考，不同系统之间存在时钟偏移。如果卫星来自多个星座，则需要额外的测量来估计系统间的时钟偏差。综上所述，需要同时跟踪至少 (N + 3) 颗卫星才能获得唯一定位的接收机，其中 N 为被跟踪卫星中的星座数量。

在收集到足够的测量数据后，将式 $\eqref{2.1}$ 中的约束条件叠加在一起，形成一系列带有未知变量 $p_r^E$ 和 $\delta t$ 的方程。对伪距测量进行校正，使其仅为 $p_r^E$ 和 $\delta t$ 的函数。利用 Saastamoinen 模型³估计对流层延迟 $T_r^s$，利用 Klobuchar 模型⁴和星历表参数计算电离层延迟 $I_r^s$。通过排除低海拔卫星，我们忽略了由多径效应引起的延迟 $M_r^s$。在实践中，将使用超过 (N + 3) 个测量值，并通过最小化残差平方和来获得解。如⁵所示，SPP 解的噪声不仅与测量噪声有关，还与卫星的几何分布有关。如下图所示一个简化的二维例子显示了卫星分布对最终解的噪声特性的影响。因此，在卫星分布均匀的情况下，即使测量噪声不变，SPP 算法的性能也会更好。

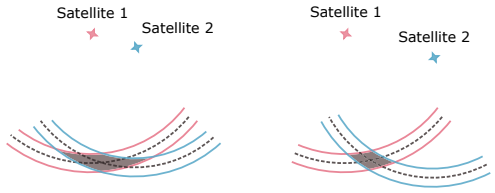
卫星分布如何影响SPP解的不确定性的简化二维插图。这里我们假设接收机与卫星之间的时间是同步的，因此两个卫星就足以进行定位。虚线表示地面真实值范围，而两条实线之间的区域表示可能的噪声测量。SPP 解的不确定性用阴影表示。

3. 系统框架

论文中提出的系统的结构如下图所示。

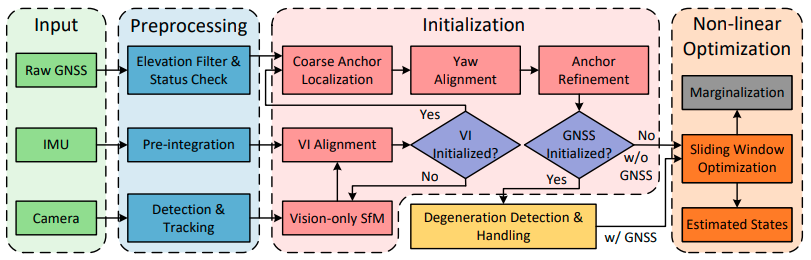
估计器将原始 GNSS、IMU 和相机测量作为输入，然后对每种类型的测量应用必要的预处理。与参考 1 ¹ 中一样，IMU 测量值是预积分，整个图像被总结为一系列稀疏特征点。对于 GNSS 原始数据，首先设置截至高度角剔除多径影响可能较大的和不健康的卫星。为了拒绝不稳定的卫星信号，只允许连续锁定一定时期的卫星进入系统。由于星历数据是通过慢速卫星接收机无线链路（50 比特/秒）获取的，因此在其相应的星历完全传输之前，GNSS 测量无法使用。在预处理阶段之后，所有的测量都为估计器做好了准备，但在进入优化部分之前，需要一个初始化阶段来正确初始化非线性估计器的系统状态。

初始化从仅视觉的 SfM 开始，从中联合估计最相似的运动和结构，然后将来自 IMU 的轨迹与 SfM 结果对齐，以恢复尺度、速度、重力和 IMU 偏差。 VI 初始化完成后，进行从粗到精的 GNSS 初始化过程。 首先通过 SPP 算法获得粗略的定位结果，然后在偏航对齐阶段使用来自 VI 初始化和 GNSS 多普勒测量的局部速度关联局部和全局框架。 最后初始化阶段以 anchor refinement 结束，它利用精确的局部轨迹并施加时钟约束来进一步细化载体的全局位置。

在初始化阶段之后，会检查并仔细处理 GNSS 退化情况，以确保稳健的性能。 然后制定来自所有测量的约束，以在非线性优化框架下联合估计滑动窗口内的系统状态。 请注意，如果 GNSS 不可用或无法正确初始化，我们的系统自然会降级为 VIO。 为了确保实时性能和处理视觉惯性退化运动，在每次优化后也也将进行边缘化策略。

4. 系统概率模型

在概率框架下制定并推导出 GVINS 状态估计问题，整个问题被组织成一个因子图，来自传感器的测量形成了一系列因子，这些因子反过来又约束了系统状态。 接下来将详细讨论概率图中的每种类型的因子。 首先先明确下一个滑动窗口内的系统状态量都包含哪些： $$ \begin{align*} {\cal X} &= [ x_0, x_1, \cdots x_n, \rho_0, \rho_1, \cdots \rho_m, \psi] \newline x_k &= [ p_{b_{t_k}}^w, v_{b_{t_k}}^w, q_{b_{t_k}}^w, b_a, b_w, \delta t, \dot{\delta t} ], \ \ k \in [0, n] \newline \delta t &= [ \delta t_G, \delta t_R, \delta t_E, \delta t_C] \end{align*} \tag{4.1} \label{4.1} $$

• 位置 $p_b^w$ 和姿态 $q_b^w$ ，速度 $v_b^w$ 、加速度 bias $b_a$ 以及陀螺仪 bias $b_w$
• n 表示滑窗的大小，m 表示在滑窗内特征点的个数，$\rho$ 为每个特征点的逆深度
• $\psi$ 表示 yaw 方向上关于局部世界坐标系与 ENU 坐标系的补偿量
• $\delta t$ 和 $\dot{\delta t}$ 分别为接收器时钟 bias 和接收器时钟漂移速率。因为系统支持四个独立的星座，因此针对 GPS、GLONASS、伽利略和北斗的时钟 bias 是分别独立估计的。而接收器时钟漂移速率只与接收端有关，因而接收器时钟漂移速率是公用的。

将最优系统状态定义为在给定所有测量值时最大似然估计（MAP）的状态。假设所有测量都相互独立，每次测量的噪声均为零平均高斯分布，MAP 问题可以进一步转化为一系列成本和最小的问题，每个代价对应于一个特定的测量。 $$ \begin{align*} {\cal X}^* &= \arg\max_{\cal X} p({\cal X} | z) \newline &= \arg \max_{\cal X} p({\cal X}) p(z | {\cal X}) \newline &= \arg \max_{\cal X} p({\cal X}) \prod_{i=1}^n p(z_i | {\cal X}) \newline &= \arg \min_{\cal{X}} \left\lbrace \lVert r_p - H_p {\cal X} \rVert^2 + \sum_{i=1}^n \lVert r(z_i, {\cal X}) \rVert_{P_i}^2 \right\rbrace \end{align*} \tag{4.2} \label{4.2} $$ 上式中，$z$ 是 $n$ 个独立传感器测量值集合，系统状态的先验因子通过 $\lbrace r_p, H_p \rbrace$ 简述，$r(\cdot)$ 表示计算各测量值的残差，而其中 $\lVert\cdot\rVert_P$ 表示为 Mahalanobis 距离。我们发现式 $\eqref{4.2}$ 适合使用因子图表示，因此将优化问题分解为与状态和测量相关的单个因子，下图显示了 GVINS 系统的因子图。除了由传感器测量结果构成的因子外，还需利用一个先验因子约束局部世界坐标系初始位姿的四个不可观方向，当进行边缘化老帧之后，该先验因子将变成一个稠密连接的复杂因子。

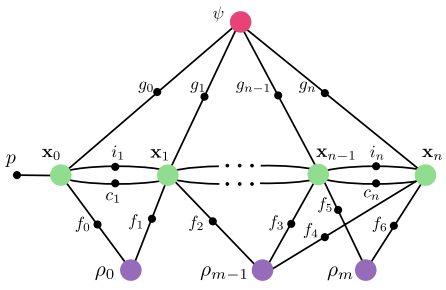
GVINS 系统中优化问题的因子图表示，其中系统状态用大彩色圆表示，因子用小黑圈表示。从各种测量中得到的因素包括惯性因子 $i$ 、视觉因子 $f$ 、伪距和多普勒因子 $g$ 和时钟因子 $c$ ，以及利用先验因子 $p$ 对局部世界坐标系的第一位姿进行约束。

关于 IMU 因子⁶、视觉因子⁷在原先的 VINS 系统中已经详细介绍过了，这里不在赘述。我们直接介绍与 GNSS 相关的因子。

4.1 伪距因子

假设 GNSS 接收机 $r$ 锁定了导航卫星 $s$ ，通过测量码移获得码伪距信息，如式 $\eqref{2.1}$ 所示。卫星时钟误差和大气延迟使用 2.3 节中描述的模型进行补偿。在 GVINS 系统中，码伪距测量噪声 $\epsilon^s_r$ 模型化为零均高斯分布: $$ \epsilon^s_r \sim {\cal N}(0, \sigma_{r,pr}^s) \ , \quad \sigma_{r, pr}^s = \frac{n_s \times n_{pr}}{\sin^2 \theta_{el}} \tag{4.3} \label{4.3} $$ 其中 $n_s$ 为广播卫星空间精度指标，$n_{pr}$ 为接收机报告的码伪距测量噪声指标。$\theta_{el}$ 在接收端表示卫星仰角，这个分母项有两个原因。首先可以抑制 GNSS 多路径效应对低海拔卫星产生的噪声；此外，导航系统广泛采用的 Klobuchar 模型得到的电离层延迟仍包含高达 50%⁴的误差。由于低空卫星存在较大的电离层延迟，采用分母项也可以减小电离层补偿带来的误差。

ECEF 坐标系中的坐标可以通过一个定位点转换为局部世界框架，ENU 坐标系就是在这个定位点上建立的。给定定位点的 ECEF 坐标，从 ENU 坐标系到 ECEF 坐标系的旋转为： $$ R_n^e = \begin{bmatrix} - \sin \lambda & - \sin \phi \cos \lambda & \cos \phi \cos \lambda \newline \quad \cos \lambda & - \sin \phi \sin \lambda & \cos \phi \sin \lambda \newline 0 & \cos \phi & \sin \phi \end{bmatrix} \tag{4.4} \label{4.4} $$ 其中，$\phi$ 和 $\lambda$ 是地理坐标系中参考点的经纬度。ENU 坐标系与局部世界坐标系之间的 1-DOF 旋转 $R_w^n$ 由偏航补偿 $\psi$ 给出。因此，ECEF 坐标系与接收机天线局部世界坐标系的关系可以表示为： $$ \begin{align*} p_r^e &= R_n^e R_w^n(p_r^w - p_{anc}^w) + p_{anc}^e \newline \text{其中}&, ,, R_w^n = \begin{bmatrix} \cos\psi & -\sin\psi & 0 \newline \sin\psi & \cos\psi & 0 \newline 0 & 0 & 1\end{bmatrix} \end{align*} \tag{4.5} \label{4.5} $$ 在实现过程中，为了方便将定位点设置为局部世界框架的原点，也就是说，局部世界框架的原点与 ENU 框架的原点重合，如图 1 所示。因此，锚点在局部世界框架中的坐标 $p_{anc}^w$ 变为零向量。接收机天线在局域坐标系中的位置可与系统状态联系起来： $$ p_r^w = p_b^w + R_b^w p_r^b \tag{4.6} \label{4.6} $$

目前为止，我们能够在给定相应系统状态的任何时刻计算出接收天线的 ECEF 坐标。由于接收端对 GNSS 测量数据进行了时间标记，因此我们定义 ECI 坐标系与 ECEF 坐标系在信号接收时间一致。这样当信号到达接收机时，有 $p_r^E = p_r^e$ 。另一方面，通过广播星历和码伪距测量可以得到信号传输时卫星在 ECEF 坐标系中的位置，将其记为 $p_s^{e’}$ 。由于地球自转的原因，信号离开卫星时的 ECEF 坐标系 $(\cdot)^{e’}$ 与信号到达时的 ECEF 坐标系 $(\cdot)^e$ 不同。因此需要把卫星的位置转换为 ECI 坐标系下（也就是信号接收时的 ECEF 坐标系），利用下式进行转换： $$ p_s^E = R_z(- w_E \cdot t_f) p_s^{e’} \tag{4.7} \label{4.7} $$ 其中 $R_z(\theta)$ 绕 ECI 坐标系 $z$ 轴旋转 $\theta$ 大小的角度，而 $t_f$ 为 GNSS 信号的 ToF。由此，在 $t_k$ 时刻一个码伪距测量因子关联系统状态有 $\lbrace p_{b_{t_k}}^w, q_{b_{t_k}}^w \delta t_k, \psi \rbrace$ 和星座 $s_j$ ，它的残差可以被定义为： $$ r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X}) = \lVert R_z(-w_E \cdot t_f) p_{s_j}^{e’} - p_{r_k}^E \rVert + c(\zeta_{s_j}^T \delta t_k - \Delta t^{s_j}) + T_{r_k}^{s_j} + I_{r_k}^{s_j} - \tilde P_{r_k}^{s_j} \tag{4.8} \label{4.8} $$ 其中 $r_k$ 代表 GNSS 接收器接接收时间戳 $t_k$ 。

4.2 多普勒频移因子

多普勒频移，如式 $\eqref{2.2}$ 所示，是由接收机与卫星之间沿信号传播路径线的相对速度导致的结果。类似于码伪距噪声，多普勒频移测量噪声 $n_{r, dp}$ 也定为零均高斯分布，对应的方差建模为 $$ \sigma_{r, dp}^s = \frac{n_s \times n_{dp}}{\sin^2 \theta_{el}} \tag{4.9} \label{4.9} $$ 其中 $n_{dp}$ 为接收机报告的测量噪声指标。在 ECEF 坐标系下的接收机速度可以由局部世界坐标系下的速度得到 $$ v_r^e = R_n^e R_w^n v_b^w \tag{4.10} \label{4.10} $$ 通过定义 ECI 坐标系为信号接受时的 ECEF 坐标系，则有 $v_r^E = v_r^e$ 。那么卫星在信号传输过程 ECEF 坐标系下的速度 $v_s^{e’}$ 可以通过下式转换到 ECI 坐标系下 $$ v_s^E = R_z( - w_E \cdot t_f ) v_s^{e’} \tag{4.11} \label{4.11} $$ 由此，在 $t_k$ 时刻一个多普勒频移因子关联系统状态有 $\lbrace p_{b_{t_k}}^w, q_{b_{t_k}}^w \delta t_k, \psi \rbrace$ 和星座 $s_j$ ，它的残差可以被定义为： $$ r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X}) = \frac 1 \lambda \kappa_{r_k}^{s_j} {^T} (v_{s_j}^E - v_{r_k}^E) + \frac c \lambda (\dot{\delta t_k} - \dot{\Delta t^{s_j}}) + \Delta \tilde f_{r_k}^{s_j} \tag{4.12} \label{4.12} $$

4.3 接收器时钟因子

GNSS 接收器时钟 bias 在 $t_k$ 到 $t_{k+1}$ 之间关联时钟漂移可以定义如下 $$ \delta t_k = \delta t_{k-1} + 1_{4 \times 1} \int_{t_{k-1}}^{t_k} \dot{\delta t} \ dt \tag{4.13} \label{4.13} $$ 其中 $1_{n \times m}$ 表示 $n \times m$ 维值全为 1 的矩阵。离散情况下的残差为

$$ r_{\cal T} (\tilde z_{k-1}^k, {\cal X}) = \delta t_k - \delta t_{k-1} - 1_{4 \times 1} \dot{\delta t} _{k-1} \tau _{k-1}^k \tag{4.14} \label{4.14} $$

这里 $\tau_{k-1}^k$ 是测量 $k-1$ 和 $k$ 之间的时间差。于此相关的协方差矩阵定义为与其离散误差对应元素描述的 $4 \times 4$ 对角矩阵 $D_{t, k}$ 。而 GNSS 接收机的时钟漂移率则是由接收机时钟的频率稳定性决定的。在低成本 GNSS 接收机中，Temperature Controlled X’tal (crystal) Oscillator (TCXO) [直译: 温控X(晶)振荡器] 是常用的时钟源。由于 TCXO 的噪声特性，接收机时钟漂移率被建模成一个随机游走过程，从而残差为

$$ r_{\cal W} (\tilde z_{k-1}^k, {\cal X}) = \dot{\delta t_k} - \dot{\delta t}_{k-1} \tag{4.15} \label{4.15} $$

相对应的方差 $\sigma_{dt, k}$ 由时钟漂移的稳定性决定。

4.4 相关雅克比

由于 GNSS 的测量并不能对齐到关键帧时刻，因此，根据 GNSS 的测量时间选取前后两个关键帧通过时间因子进行插值构建上述与 GNSS 测量模型相关的优化因子们。

在作者的源码中，伪距因子关于 $p_r^b$ 似乎直接默认为 $0$ (估计由于硬件系统设计，该值很小 [小于伪距噪声量级]，如果实际硬件该值很大则不能为 $0$ ，这个时候是需要进行杆臂补偿的)，因此雅克比关于旋转姿态的量直接设为 $0$ (即使 $p_r^b$ 不为 $0$，关于旋转分量的雅克比也会设置为 0，这是因为这个时候的旋转姿态量是插值来的，且伪距测量的噪声太大，对旋转姿态也起不到很好的约束)。与伪距因子和多普勒频移因子相关的源码主要位于 gnss_psr_dopp_factor.cpp 文件中。下面对伪距因子和多普勒因子的雅克比进行推导说明。另外代码中多了一个权重项，这是因为 Ceres 优化器只能处理传统的最小二乘运算，并不能添加信息矩阵作为马氏距离的权重到优化迭代中。雅克比的推导部分参考了⁸⁹ 。

4.4.1 伪距因子对于 $p_{b_i}^w, \ p_{b_j}^w$ 的雅克比

首先根据式 $\eqref{4.5} \eqref{4.6} \eqref{4.7}$ 得：$p_{r_k}^E = R_n^e R_w^n p_{b_k}^w + p_{anc}^e$ 代入式 $\eqref{4.8}$ 得

$$ r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X}) = \lVert R_z(-w_E \cdot t_f) p_{s_j}^{e’} - R_n^e R_w^n p_{b_k}^w - p_{anc}^e \rVert + c(\zeta_{s_j}^T \delta t_k - \Delta t^{s_j}) + T_{r_k}^{s_j} + I_{r_k}^{s_j} - \tilde P_{r_k}^{s_j} \tag{4.16} \label{4.16} $$

为了后续推导方便，令 $K = R_z(-w_E \cdot t_f) p_{s_j}^{e’} - R_n^e R_w^n p_{b_k}^w - p_{anc}^e$ ，则有：

$$ \begin{align*} \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_k}^w} &= \frac{\partial \lVert K \rVert}{\partial p_{b_k}^w} = \frac{\partial ( K^T K)^{1/2} }{\partial p_{b_k}^w} = \frac{\partial ( K^T K)^{1/2} }{\partial (K^T K)} \cdot \frac{\partial (K^T K) }{\partial K} \cdot \frac{\partial K}{\partial p_{b_k}^w} \newline &= \frac12 (K^T K)^{-1/2} \cdot 2K^T \cdot (-R_n^e R_w^n) \newline &= -\bigg(\frac{K}{\lVert K \rVert}\bigg)^T R_n^e R_w^n \newline &= - \kappa_r^{sT} R_n^e R_w^n \end{align*} \tag{4.17}\label{4.17} $$

然后根据时间戳进行线性插值获取接收机接对应测量时刻的位置 $p_{b_k}^w = {\rm ratio} * p_{b_i}^w + (1 - {\rm ratio})*p_{b_j}^w$ ，因此有：

$$ \begin{align*} \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_i}^w} &= \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_k}^w} \cdot \frac{\partial p_{b_k}^w}{\partial p_{b_i}^w} = - \kappa^s_r {}^T R_n^e \ R_w^n * {\rm ratio} \newline \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_j}^w} &= \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_k}^w} \cdot \frac{\partial p_{b_k}^w}{\partial p_{b_j}^w} = - \kappa^s_r {}^T R_n^e \ R_w^n * (1 - {\rm ratio}) \end{align*} \tag{4.18}\label{4.18} $$

4.4.2 伪距因子对于 $\psi$ 的雅克比

参照式 $\eqref{4.16} \eqref{4.17}$ 的求导过程有：

$$ \begin{align*} \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial \psi} &= \frac{\partial \lVert K \rVert}{\partial \psi} = \frac{\partial ( K^T K)^{1/2} }{\partial \psi} = \frac{\partial ( K^T K)^{1/2} }{\partial (K^T K)} \cdot \frac{\partial (K^T K) }{\partial K} \cdot \frac{\partial K}{\partial \psi} \newline &= \frac12 (K^T K)^{-1/2} \cdot 2K^T \cdot (-R_n^e \dot R_w^n p_{b_k}^w) \newline &= - \kappa_r^{sT} R_n^e \dot R_w^n p_{b_k}^w \newline \text{其中}, , \dot R_w^n &= \begin{bmatrix} -\sin\psi & -\cos\psi & 0 \newline \cos\psi & -\sin\psi & 0 \newline 0 & 0 & 0 \end{bmatrix} \end{align*} \tag{4.19}\label{4.19} $$

4.4.3 伪距因子对于 $p_{anc}^e$ 的雅克比

参照式 $\eqref{4.16} \eqref{4.17}$ 的求导过程有： $$ \begin{align*} \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{anc}^e} &= \frac{\partial \lVert K \rVert}{\partial p_{anc}^e} = \frac{\partial ( K^T K)^{1/2} }{\partial p_{anc}^e} = \frac{\partial ( K^T K)^{1/2} }{\partial (K^T K)} \cdot \frac{\partial (K^T K) }{\partial K} \cdot \frac{\partial K}{\partial p_{anc}^e} \newline &= \frac12 (K^T K)^{-1/2} \cdot 2K^T \cdot (-1) \newline &= - \kappa_r^{sT} \end{align*} \tag{4.20}\label{4.20} $$

4.4.4 伪距因子对于 $\delta t$ 的雅克比

$$ \frac{\partial r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X})}{\partial \delta t} = c\zeta_{s_j}^T \tag{4.21}\label{4.21} $$

对时间因子的导数需要注意的是作者在代码中，对时间因子的估计状态量进行了调整，所有对应的雅克比也稍微有点不同，但都是线性的，很容易得到。

4.4.5 多普勒因子对于 $p_{b_i}^w, \ p_{b_j}^w$ 的雅克比

多普勒因子对于 $p_{b_i}^w, \ p_{b_j}^w$ 的雅克比的推导是一个较为繁琐的过程，首先其中根据式 $\eqref{2.3}$ 有：（下面推导过程中需要用到 ¹⁰ 中部分公式） $$ \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_{i/j}}^w} = \frac 1 \lambda (v_{s_j}^E - v_{r_k}^E)^T \frac{\partial \kappa_r^{s}}{\partial p_{r_k}^E} \frac{\partial p_{r_k}^E}{\partial p_{b_{i/j}}^w} \tag{4.22}\label{4.22} $$ 根据式 $\eqref{4.17} \eqref{4.18}$ 得： $$ \begin{align*} \frac{\partial p_{r_k}^E}{\partial p_{b_i}^w} &= R_n^e \ R_w^n * {\rm ratio} \newline \frac{\partial p_{r_k}^E}{\partial p_{b_j}^w} &= R_n^e \ R_w^n * (1 - {\rm ratio}) \end{align*} \tag{4.23}\label{4.23} $$ 麻烦的是对式 $\eqref{4.22}$ 中链式第一部分的求导，其中根据式 $\eqref{4.12}$ 有， $$ \begin{align*} \frac{\partial \kappa_r^{s}}{\partial p_r^E} &= \frac{\partial \big( \frac{p_s^E - p_r^E}{\lVert p_s^E - p_r^E \rVert} \big)}{\partial p_r^E} = \frac{\partial \big( \frac{p_s^E - p_r^E}{\sqrt{(p_s^E - p_r^E)^2}} \big)}{\partial p_r^E} \newline \text{令} ,, p &= p_s^E - p_r^E = \begin{bmatrix} x \newline y \newline z \end{bmatrix},,\text{有:} \newline \frac{\partial \kappa_r^{s}}{\partial p_r^E} &= \frac{\partial \big( \frac{p}{\sqrt{p^T p}} \big)}{\partial p} \cdot \frac{\partial p}{\partial p_r^E} \newline &= \bigg(\frac{1}{\sqrt{p^T p}} \cdot I_{3\times3} + p \cdot \frac{\partial \frac1{\sqrt{p^T p}}}{\partial p} \bigg) \cdot (-I_{3\times3}) \newline &=-\bigg( \frac{1}{\sqrt{p^T p}} \cdot I_{3\times3} + p \cdot \frac{0 - \frac12 (p^T p)^{-1/2} \cdot 2p^T}{p^T p} \bigg) \cdot (-I_{3\times3}) \newline &= - \frac{1}{(p^T p)^{3/2}} (p^T p \cdot I_{3\times3} - pp^T) \newline &= - \frac1{(x^2 + y^2 + z^2)^{3/2}} \left( \begin{bmatrix} (x^2 + y^2 + z^2)^{3/2} & & \newline & (x^2 + y^2 + z^2)^{3/2} & \newline & & (x^2 + y^2 + z^2)^{3/2} \end{bmatrix} - \begin{bmatrix} x^2 & xy & xz \newline yx & y^2 & yz \newline zx & zy & z^2 \end{bmatrix} \right) \newline &= - \frac1{(x^2 + y^2 + z^2)^{3/2}} \begin{bmatrix} y^2 + z^2 & -xy & -xz \newline -yx & x^2 + z^2 & -yz \newline -zx & -zy & x^2 + y^2 \end{bmatrix} \end{align*} \tag{4.24}\label{4.24} $$

结合$\eqref{4.22} \eqref{4.23} \eqref{4.24}$ 有： $$ \begin{align*} \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_{i}}^w} &= \frac 1 \lambda (v_{s_j}^E - v_{r_k}^E)^T \left(- \frac1{(x^2 + y^2 + z^2)^{3/2}} \begin{bmatrix} y^2 + z^2 & -xy & -xz \newline -yx & x^2 + z^2 & -yz \newline -zx & -zy & x^2 + y^2 \end{bmatrix} \right) R_n^e \ R_w^n * {\rm ratio} \newline \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial p_{b_{j}}^w} &= \frac 1 \lambda (v_{s_j}^E - v_{r_k}^E)^T \left(- \frac1{(x^2 + y^2 + z^2)^{3/2}} \begin{bmatrix} y^2 + z^2 & -xy & -xz \newline -yx & x^2 + z^2 & -yz \newline -zx & -zy & x^2 + y^2 \end{bmatrix} \right) R_n^e \ R_w^n * (1 - {\rm ratio}) \newline {\text 其中,}\quad & p = p_s^E - p_r^E = \begin{bmatrix} x & y & z \end{bmatrix}^T \end{align*} \tag{4.25} \label{4.25} $$

4.4.6 多普勒因子对于 $v_{b_i}^w, \ v_{b_j}^w$ 的雅克比

首先根据 $\eqref{4.10} \eqref{4.12}$ 易得： $$ \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial v_{b_k}^w} = - \frac1\lambda \kappa_{r_k}^{s_j} {^T} R_n^e R_w^n \tag{4.26} \label{4.26} $$ 根据时间戳进行线性插值获取接收机接对应测量时刻的速度 $v_{b_k}^w = {\rm ratio} * v_{b_i}^w + (1 - {\rm ratio})*v_{b_j}^w$ ，因此有

$$ \begin{align*} \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial v_{b_i}^w} &= \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial v_{b_k}^w} \frac{\partial v_{b_k}^w}{\partial v_{b_i}^w} = - \frac1\lambda \kappa_{r_k}^{s_j} {^T} R_n^e R_w^n * \rm{ratio} \newline \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial v_{b_j}^w} &= \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial v_{b_k}^w} \frac{\partial v_{b_k}^w}{\partial v_{b_j}^w} = - \frac1\lambda \kappa_{r_k}^{s_j} {^T} R_n^e R_w^n * (1- \rm{ratio}) \end{align*} \tag{4.27} \label{4.47} $$

4.4.7 多普勒因子对于 $\psi$ 的雅克比

根据 $\eqref{4.10} \eqref{4.12}$ 易得： $$ \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial \psi} = - \frac1\lambda \kappa_{r_k}^{s_j} {^T} R_n^e \dot R_w^n v_{b_k}^w \tag{4.28} \label{4.28} $$

其中 $\dot R_w^n$ 如 $\eqref{4.19}$ 所示。

4.4.8 多普勒因子对于 $\dot{\delta t}$ 的雅克比

根据 $\eqref{4.12}$ 易得： $$ \frac{\partial r_{\cal D}(\tilde z_{r_k}^{s_j}, {\cal X})}{\partial \dot{\delta t}} = - \frac c\lambda \tag{4.29} \label{4.29} $$ 对时间因子的导数需要注意的是作者在代码中，对时间因子的估计状态量进行了调整，所有对应的雅克比也稍微有点不同，但都是线性的，很容易得到。

5. GNSS 初始化和退化

上一节中所述的状态估计过程相对于系统状态是非线性的，因此其性能在很大程度上依赖于初始值。通过在线初始化，初始状态可以从未知情况中恢复，而无需任何假设或手动干预。在系统运行期间，估计器也可能遇到不完美的情况，其中一些传感器出现故障或退化。由于关于视觉惯性系统的初始化和退化问题已经有大量的文献，在本节中，我们将范围限制在 GNSS 部分。在下面，我们首先介绍了所提出的粗到细的GNSS初始化方法，然后我们讨论了降低我们系统性能的几种场景。

5.1 GNSS 初始化

如前所述，需要一个具有已知全局和局部坐标的点来融合全局 GNSS 测量与局部视觉和惯性信息。由于该点已经设置为局部世界坐标系的原点，因此需要事先对局部世界原点的 ECEF 坐标进行校准。此外， ENU 与局部世界坐标系之间的偏航补偿 $\psi$ 也需要一个合理的初始化值，使系统在非线性优化阶段阶段收敛。在本文中，提出了一个多级 GNSS-VI 初始化程序来在线校准目位点和偏航补偿。在 GNSS-VI 初始化之前，我们假设 VIO 已成功初始化，即重力矢量、初始速度、初始 IMU 偏差和尺度已获得初始值。 之后，在局部世界坐标系中形成一条平滑的轨迹，并准备在 GNSS-VI 初始化阶段使用。GNSS-VI 初始化程序要求至少跟踪 4 颗卫星（如果所有卫星都属于单个星系；否则要求为 $(N+3)$ 颗，当涉及 N 个卫星系统）。此外，为了获得可靠的初始量，还要求最小运动距离为 4 米。如下图所示，在线 GNSS-VI 初始化以粗到细的方式进行，包括以下三个步骤：

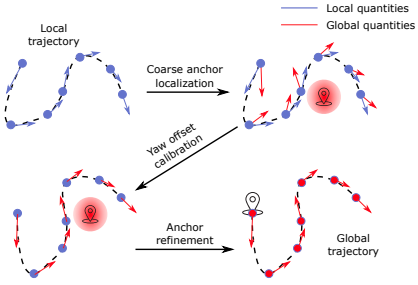
GNSS 由粗到精初始化模块，该模块获取 VIO 的局部世界坐标系下的位置和速度结果，并在全局 ECEF 坐标系中输出相应的轨迹。

5.1.1 锚点粗略定位

首先，由 GNSS SPP 算法在没有任何先验信息的情况下生成一个粗略 ECEF 坐标。SPP 算法将滑动窗口的所有伪距测量作为输入。由于滑动窗口内的测量值是时间和空间跨度的，因此来自 SPP 的结果是当前窗口的平均位置。

5.1.2 偏航角补偿标定

其次，通过低噪声的多普勒频移测量标定出关于 ENU 坐标系与局部世界坐标系的偏航角补偿初始值。初始的偏航补偿值与接收器时钟偏移速率可以通过下面这个优化问题求解得到： $$ \underset{\dot{\delta t},\ \psi}{\rm minimize} \sum_{k=1}^n \sum_{j=1}^{p_k} \left \lVert r_{\cal D} (\tilde z_{r_k}^{s_j} , {\cal X}) \right \rVert_{\sigma_{r_k}^{s_j}, \ dp}^2 \tag{5.1}\label{5.1} $$ 其中 $n$ 是窗口的大小，而 $p_k$ 是窗口内第 $k$ 个时期观测到的卫星数。在窗口内假设速度 $v_b^w$ 固定为 VIO 的估计结果，且 $\dot{\delta t}$ 恒定。由于方向向量 $\kappa_r^s$ 和旋转 $R_n^e$ 对接收机的位置不敏感，因此通过利用第一步得到的粗锚坐标来计算得到的 $\kappa_r^s$ 和 $R_n^e$ 是足够充分的。由此，估计参数仅包括整个滑窗测量的偏航误差 $\psi$ 和平均时钟偏移速率 $\dot{\delta t}$ 。最后对 ENU 坐标系与局部世界坐标系之间的转换进行充分标定估计。

5.1.3 锚点精细化

最后，对第一步估计的粗锚点进行精细化，并将局部世界坐标系轨迹与 ECEF 坐标系中的轨迹对齐。与第一步不同的是，使用 VIO 的位置结果作为先验信息，利用下式优化模型，在滑动窗口测量中精细化估计值 $$ \underset{\delta t, \ p_{anc}^e}{\rm minimize} \left( \sum_{k=1}^n \sum_{j=1}^{p_k} \big\lVert r_{\cal P} (\tilde z_{r_k}^{s_j}, {\cal X}) \big\rVert_{\sigma_{r_k ,\ pr}^{s_j}}^2 + \sum_{k=1}^n \big\lVert r_{\cal T} (\tilde z_{k-1}^k, {\cal X}) \big\rVert_{D_{t,\ k}}^2 \right) \tag{5.2}\label{5.2} $$ 对上式进行优化估计之后，我们可以利用初始化历来每一个 GNSS 测量进行精细化锚点与接收器时钟 bias 。在这一步之后，定位锚点（ENU 坐标系原点）被设置为局部世界坐标系原点。最后，整个估计器的初始化阶段结束，所有必要的量都被赋予了初始值。

5.2 GNSS 退化

毫无疑问，我们的融合系统将在 GNSS 信号稳定、卫星分布良好的开放区域内表现最好。下面，讨论几种可能降低系统性能的情况。

5.2.1 低速运动

由于多普勒频移测量的噪声水平比伪距低一个数量级，局部世界坐标系和 ENU 坐标系之间的偏航偏移可以通过多普勒频移测量的短窗口得到很好的约束。 一旦 GNSS 接收机的速度低于多普勒频移的噪声水平，估计的偏航偏移可能会被测量噪声破坏。 此外，低速移动也意味着窗口内的平移距离较短，因此偏航估计也可能受到伪距的影响。 在平台仅进行旋转运动的极端情况下，GNSS 无法提供有关旋转方向的任何信息，并且偏航分量将像 VIO 中那样漂移。 因此，如果窗口内的平均速度低于阈值 $v_{ths}$，则就固定偏航偏移变量。在我们的系统中， $v_{ths}$ 设置为 $0.5 m/s$，即使是行人也可以轻松满足。

5.2.2 被跟踪的卫星少于 4 个

如果被跟踪的卫星数量少于 4 个，则 SPP 或松耦合方法将无法解决接收机的位置。然而，在紧耦合结构的帮助下，我们的系统仍然能够利用可用的卫星，并随后更新状态向量。关于各种卫星配置下的性能退化研究更为详尽的结束，感兴趣的可以约定原文。

5.2.3 无 GNSS 信号

在 GNSS 信号完全不可用的室内或杂乱环境中，与全局信息相关的状态，即偏航偏移 $\psi$、接收机时钟偏差 $\delta t$ 和漂移率 $\dot{\delta t}$ 不再可观测。 然而，在优化过程中仍然保留了式 $\eqref{4.14}$ 和式 $\eqref{4.15}$ 中的约束。正如我们在接收机静止分析中发现的那样，低成本接收机的时钟漂移率非常稳定，因此（接近）最佳时钟漂移率由约束式 $\eqref{4.15}$ 的约束维持。 类似地，接收机的 bias 通过式 $\eqref{4.14}$ 约束传播，当重新捕获 GNSS 信号时，它反过来提供一个良好的初始值。 当 GNSS 信号变化无常时，这种机制提高了我们融合系统的稳定性，并消除了在信号丢失和重新捕获时重新初始化的问题。

Reference