Camera - Lidar 标定

Extrinsic Calibration Of Camera and Lidar

通常，标定激光和相机之间的外参数有两类方法：一类是利用 3D-3D 的约束，即利用激光测量的三维激光点 (3D) 和相机测量的标定板三维坐标 (3D) 两者来构建约束；另一类是利用 3D-2D 的约束，即利用激光测量的三维激光点 (3D) 和图像二维特征（2D、点特征、线段特征）来构建约束。下文主要讲解利用 3D-3D 约束来进行外参数标定的方法。标定过程的通常做法是先利用少量观测求解外参数的初始值，然后利用多帧数据的约束进行最小二乘优化对初始值进行 refine ¹。

1. 基于平面约束的激光标定算法

如 Fig. 1 所示，相机可以通过标定板平面的二维码或棋盘格来计算标定板平面在相机坐标系下的表示。同时，激光发出的光束落在标定板平面上（图中红点），利用激光点在激光坐标系下的坐标和平面方程在相机坐标系下的坐标，构建点在平面上的约束从而求解外参数。¹²³

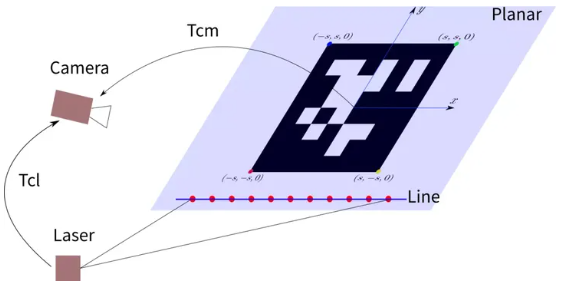
Fig. 1: 基于平面约束的激光标定算法示意图

1.1 平面约束

假设标定板平面在相机坐标系 $c$ 中的参数为 $\pi^c = [\mathbf n^c, d] \in \mathbb R^4$，其中 $\mathbf n^c \in \mathbb R^3$ 是平面的三维法向量， $d$ 是相机坐标系原点到平面的距离。平面上的一个三维点在相机坐标系下的坐标为 $P^c \in \mathbb R^3$，点在平面上满足 $$ \mathbf n^c {}^\top P^c + d = 0 \tag{1} \label{1} $$ 假设从激光坐标系 $l$ 到相机坐标系 $c$ 之间的旋转和平移为 $R_{cl}$ 和 $\mathbf t_{cl}$ 。如果知道激光坐标系中某个激光点 $P^l$ 落在标定板上，则通过点在平面上这个约束能够构建关于外参数的方程 $$ \mathbf n^c {}^T (R_{cl} P^l + \mathbf t_{cl}) + d^c = 0 \tag{2} \label{2} $$ 上述方程能够提供一个约束，通过多个这样的约束就能求解外参数。求解时，一个直观的想法是利用 g2o 或者 ceres 等优化工具构建非线性最小二乘进行优化求解。但是对于非线性最小二乘问题，需要知道外参数的一个初始值，如果初始值不准确，则有可能会优化到局部最小值。因此，一个合理的求解流程应该是闭式解提供初始值，对该初始值利用多帧数据进行优化，得到更准确的标定结果。

虽然平面约束对于 2D 激光和 3D 激光而言是一样的，但 2D 激光和 3D 激光闭式求解外参数的方式稍有不同。因为 3D 激光的激光点更多，从而可以直接计算激光点云的法向量，利用这个法向量简化外参数计算流程，下文将详述。接下来，介绍 2D 激光和 3D 激光与相机外参数的求解。

2. 2D 激光和相机外参数初始值求解

2.1 方式 1 : 近似直接求解法

第一种求解方式参考于 ² 论文。该方式以类似 DLT 的方式计算 $H$ ，并将计算结果因式分解为旋转 $R$ 和平移 $\bf t$ 。论文中估计的参数为从相机坐标系 $c$ 到激光坐标系 $l$ 的变换矩阵 $\lbrace R_{lc},\mathbf t_{lc}\rbrace$ 。考虑激光为 2D 激光，激光束形成的平面不妨假设为 $\rm xy$ 平面，即 $z = 0$ ，此时有 $P^l = [x, y, 0]^T$ ，结合 1.1 中的内容，坐标系变换可以写成更紧凑的形式

$$ P^c = R_{lc}^\top \left( \begin{bmatrix} x \newline y \newline 0 \end{bmatrix} - \mathbf t_{lc} \right) = \underbrace{ R_{lc}^\top \begin{bmatrix} 1 & 0 & \newline 0 & 1 & -\mathbf t_{lc} \newline 0 & 0 & \end{bmatrix} }_H \begin{bmatrix} x \newline y \newline 1 \end{bmatrix} = H \bar P^l \tag{3} \label{3} $$

结合 $\eqref{1}\eqref{3}$ ，可以得到一个简洁紧凑的形式

$$ \mathbf n^c {}^\top H \bar P^l = -d^c \tag{4} \label{4} $$

如果把 $3\times3$ 的 $H$ 矩阵当做新的未知量（ 9 个参数）进行估计，那上述约束就变成了一个线性最小二乘问题。对于单线激光而言，一帧激光可以提供两个有效约束（直线上两个点在平面上即能确定直线在平面上），因此需要大于等于 5 帧激光（不同姿态）以获取 10 个以上的约束，来求得 9 参数的 $H$ 。然后恢复出 $\lbrace R_{lc},\mathbf t_{lc}\rbrace$ $$ \begin{align*} R_{lc} &= \begin{bmatrix}\mathbf h_1 & \mathbf h_2 & \mathbf h_1 \times \mathbf h_2 \end{bmatrix}^\top \newline t_{lc} &= -\begin{bmatrix}\mathbf h_1 & \mathbf h_2 & \mathbf h_1 \times \mathbf h_2 \end{bmatrix}^\top \mathbf h_3 \end{align*} \tag{5} \label{5} $$ 不幸的是，直接因式分解并不能提供有效的旋转矩阵 $R$ （不满足旋转矩阵的性质 $R^\top R = I_{3\times3}$ ），而需要对 $SO(3)$ 进行非最佳投影。假设期望的旋转矩阵为 $\hat R_{lc}$ ，则可以通过计算带约束的最小化 Frobenius norm 问题来估计 $\hat R_{lc}$ $$ \arg\min \lVert \hat R_{lc} - R_{lc} \rVert \quad s.t. \ \hat R_{lc}^\top \hat R_{lc} = I_{3\times3} \tag{6} \label{6} $$

通俗的讲，上面这个方程的含义为：找一个最接近 $R_{lc}$ 又满足旋转矩阵质 $R^\top R = I_{3\times3}$ 的矩阵 $\hat R_{lc}$ 作为外参数。对于上述方程的求解，实际上有闭式解，可以参考文献 ⁴ 。正如文献 ⁴ 指出的，上述方式求解的精度不高，实际应用过程并不推荐。

2.2 方式 2 : 双空间配准 (Registration in the dual space)

方式一由于矩阵 $H$ 有 9 个未知量，因此估计需要 $N \ge 5$ 个校准平面并且校准算法是非最小化和非最优的，这往往会导致错误的结果。优雅的方式应该是直接闭式求解 6 自由度的外参数，即旋转矩阵只用 3 个参数而不是上述方法中先估计 9 个参数。参考文献 ³ 给出了一种闭式求解 6 自由度外参数的方法，由于估计的参数为 6 ，因此需要的最少激光观测变成了 3 帧（每帧提供两个有效约束）。

从相机坐标系 $c$ 到激光坐标系 $l$ 的变换矩阵可以如下式定义

$$ \begin{bmatrix} P^l \newline 1 \end{bmatrix} = \underbrace{ \begin{bmatrix} R_{lc} & \mathbf t_{lc} \newline \mathbf 0_3^\top & 1 \end{bmatrix} } _{T _{lc}} \begin{bmatrix} P^c \newline 1 \end{bmatrix} \tag{7} \label{7} $$

假设标定板平面在相机坐标系 $c$ 中的平面法向量齐次坐标为 $\Pi^c = [\mathbf n^c, 1] \in \mathbb R^4$，其中 $\mathbf n^c \in \mathbb R^3$ 是平面的三维法向量。双空间配准求解的思路是：将线拟合到激光点上，并将问题表述为一组共面线 $L_i^l$ 与一组平面 $\Pi_i^c$ 的三维配准。换句话说，我们的目标是找到旋转 $R_{lc}$ 和平移 $t_{lc}$，使式 $\eqref{8}$ 给出的平面 $\Pi_i^l$ 经过线 $L_i^l$ 。

$$ \Pi_i^l = \underbrace{ \begin{bmatrix} R_{lc} & \bf 0_3 \newline -\mathbf t_{lc}^\top R_{lc} & 1 \end{bmatrix} } _{T _{lc}^{-\top}} \Pi_i^c \tag{8} \label{8} $$

众所周知，点和平面是 3D 中的对偶实体 (dual entities) ，射影空间 $\mathcal P^3$ 中的平面表示为对偶空间 $\mathcal P^{3^* }$ 中的点，反之亦然。 因此，如 Fig. 2(a) 所示，方程 $\eqref{8}$ 可以理解为 $\mathcal P^{3^* }$ 中的投影变换，将点 $\Pi_i^c$ 映射到点 $\Pi_i^l$ 。在该小结后文中，如果没有特别说明，我们将根据对偶空间进行推理，以导出所需的配准算法。

$\mathcal P^3$ 中的线 $L_i^l$ 的对偶是 $\mathcal P^{3^* }$ 中的线 $L_i^{l^*}$ ，在 Plücker 坐标中的表示是

$$ L_i^{l^*} \sim \begin{bmatrix} \mathbf v_i^l \newline \mathbf u_i^l \end{bmatrix} \tag{9} \label{9} $$

其中 3 维向量 $\mathbf u_i^l$ 和 $\mathbf v_i^l$ 表示原直线 $L_i^l$ 的方向和动量 (direction and momentum) ， $L_i^{l^* }$ 上的通用点 $\Pi_i^l$ 是包含直线 $L_i^l$ 的平面的对偶表示。此外，由于 2D 激光束检测到的线 $L_i^l$ 必然是共面的，因此对偶线 $L_i^{l^*}$ 一定相交于表示激光扫描平面的点 $\Sigma^l$ 。

外参标定问题转化为在对偶空间中找到变换 $T_{lc}^{-\top}$ ，将以相机坐标表示的点 $\Pi_i^c$ 映射到2D 激光束检测到的线 $L_i^l$ 中的点 $\Pi_i^l$ （见 Fig. 2(a) ）。后者显然是以激光坐标表示的校准平面的对偶表示。等式 $\eqref{8}$ 中的变换 $T_{lc}^{-\top}$ 可以分解为两种不同的变换：

1. 一个将点 $\Pi_i^c$ 映射到点 $\hat\Pi_i^c$ 的旋转 $M$ ，如 Fig. 2(a) 所示 $$ \hat\Pi_i^c \sim \begin{bmatrix} R_{lc} & \bf 0 \newline \bf 0^\top & 1 \end{bmatrix} \Pi_i \tag{10} \label{10} $$ 旋转必须使得由 $\hat\Pi_i^c$ 和对偶空间 $O^{c^}$ 的原点定义的每条线 $W_i$ 与相应的线 $L_i^{l^ }$ 相交。

2. 将点 $\hat\Pi_i^c$ 沿线 $W_i$ 移动以将其映射为点 $\Pi_i^l$ 的平移变换 $S$ $$ \Pi_i^l \sim \begin{bmatrix} I_{3\times3} & \bf 0_3 \newline -\mathbf t_{lc}^\top & 1 \end{bmatrix} \hat\Pi_i^c \tag{11} \label{11} $$ 其中 $I_{3\times3}$ 是一个 $3 \times 3$ 的单位矩阵。

接下来的两个小节将展示如何通过 $N = 3$ 个平面和共面线之间的对应关系来估算 $M$ 和 $S$ 。

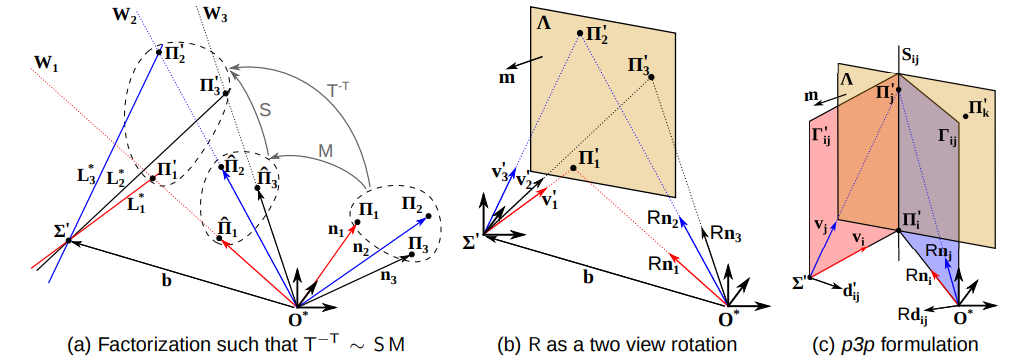
Fig. 2: 在对偶射影空间 $\mathcal P^{3^* }$ 中进行推理，用于估计将 $N = 3$ 个平面 $\Pi_i^c$ 与 $N = 3$ 条共面线 $L_i^l$ 对齐的变换 $T_{lc}^{-\top}$ 。(a) $T_{lc}^{-\top}$ 可以分解为旋转 $M$ （使旋转后的线段 $W_i$ 与线段 $L_i^{l^* }$ 相交）和平移变换 $S$ （使旋转后的点 $\hat\Pi_i^c$ 与交点 $\Pi_i^l$ 重合）; (b) 计算旋转相当于估计已知基线 $\bf b$ 的两个视图之间的相对方向（我们认为在以 $O^{c^*}$ 和 $\Sigma^l$ (2D 激光束形成的平面) 为中心的坐标系上彼此平行）；(c) 通过观察平面 $\Gamma$、$\Gamma’$ 和 $\Lambda$ 位于同一笔画中（相交与同一直线），将 $R$ 的估计公式化为 p3p 问题。

2.2.1 旋转变换

由于线 $L_i^{l^* }$ 是共面向的对偶表示，因此它们在 $\mathcal P^{3^* }$ 中定义了一束穿过 $\Sigma^l$ 的笔画线。在不失一般性的前提下，我们假设 2D 激光束参考系的原点从不位于扫描平面内，并且 $\Sigma^l$ 具有以下投影表示 $$ \Sigma^l \sim \begin{bmatrix} \bf b \newline 1\end{bmatrix} \tag{12} \label{12} $$ 通过将对偶点 $\Pi_i^c$ 与坐标系 $O^{c^* }$ 的原点连接起来可以得到第二束笔画线（见 Fig. 2(a) ）。 目标是找到绕经过 $O^{c^*}$ 的轴的旋转，从而使第二束笔画线与第一束笔画线相交。

2.2.1.1 $R$ 为两个虚拟视图之间的相对旋转

我们可以把 Fig. 2(a) 中的两束笔画线看作两个针孔摄像机，其投影中心分别位于 $\Sigma^l$ 和 $O^{c^* }$ 。这样，找到旋转 $R$ 使线 $W_i$ 与线 $L_i^{l^* }$ 相交的问题，在几何上就等同于在已知基线方向的情况下确定两个虚拟视图之间的相对方向（ Fig. 2(b) ）。Moriya 和 Takeda 在 ⁵ 中展示了如何根据图像之间 $N = 3$ 点的对应关系计算 $R$ 来解决了这一问题。

在该例子中，虚拟视图 $O^{c^* }$ 中图像点的投影坐标由向量 $\mathbf n_i^c$ 给出。 这些向量是标定平面 $\Pi_i^c$ 的法线方向。同样，虚拟视图 $\Sigma^l$ 中的图像点由向量 $\mathbf v_i^l$ 给出，这些向量与 2D 激光束检测到的线 $L_i^l$ 的矩量相对应 ($\eqref{9}$) 。基线方向由 $\eqref{12}$ 中提供的激光扫描平面的投影坐标定义。Fig. 2(b) 展示了这种几何结构，其中中心位于 $\Sigma^l$ 的局部参照系与原点位于 $O^{c^*}$ 的世界坐标系平行。

下一小节将对 ⁵ 中提出的解决方案进行另一种更直观的推到，并说明如何通过 $N = 3$ 个对应点 $\mathbf n_i^c$ ， $\mathbf v_i^l$ 确定相对方向 $R$，这些对应点被解释为两个虚拟视图中的图像点，它们被一条方向为 $\bf b$ 的基线隔开。

2.2.1.2 通过求解 P3P 问题来确定 $R$

如果相对方向 $R$ 已知，则方向为 $\mathbf v_i^l$ 和 $R_{lc} \mathbf n_i^c$ 的反投影线与 3D 点 $\Pi_i^l$ 相交，如 Fig. 2(b) 所示。因此，如果考虑 $N = 3$ 个对应关系，将获得唯一定义一个平面的 3 个点。 设 $\Lambda$ 为这个平面，用世界坐标表示为： $$ \Lambda \sim \begin{bmatrix} \bf m \newline 1 \end{bmatrix} \tag{13} \label{13} $$

现在考虑其中的两个点： $\Pi_i^l$ 和 $\Pi_j^l$ ，它们定义了三维直线 $S_{ij}$，如 Fig. 2(c) 所示。让 $\Gamma_{ij}$ 成为包含 $S_{ij}$ 和原点 $O^{c^* }$ 的平面。不难看出， $\Gamma_{ij}^c$ 的法向量一定是 $R_{lc} \mathbf d_{ij}^c$ ，且 $$ \mathbf d_{ij}^c \sim \mathbf n_i \times \mathbf n_j \tag{14} \label{14} $$ 考虑到该平面包含 $O^{c^*}$ ，因此它在世界坐标中的投影表示为 $$ \Gamma_{ij}^c \sim \begin{bmatrix} R_{lc} \mathbf d_{ij}^c \newline 0 \end{bmatrix} \tag{15} \label{15} $$ 同样，直线 $S_{ij}$ 和点 $\Sigma^l$ 定义了一个平面 $\Gamma_{ij}^l$ ，其法向量为

$$ \mathbf d_{ij}^l \sim \mathbf v_i^l \times \mathbf v_j^l \tag{16} \label{16} $$ 从 $\eqref{12}$ 可以得出， $\Gamma_{ij}^l$ 在世界坐标中的投影表示为 ： $$ \Gamma_{ij}^l \sim \begin{bmatrix} \mathbf d_{ij}^l \newline -\mathbf b^\top \mathbf d_{ij}^l \end{bmatrix} \tag{17} \label{17} $$ 直线 $S_{ij}$ 定义了一个平面的一维笔画，它不仅包含 $\Gamma_{ij}^c$ 和 $\Gamma_{ij}^l$ ，还包含经过三个重建点的平面 $\Lambda$ 。因此，由于 $\Gamma_{ij}^c$ 和 $\Gamma_{ij}^l$ 总是不同的平面，可以作为笔画的投影基础，因此存在一对标量 $\alpha_{ij}$ 和 $\beta_{ij}$，使得下面的条件成立： $$ \Lambda \sim \alpha_{ij} \Gamma_{ij}^c + \beta_{ij} \Gamma_{ij}^l \tag{18} \label{18} $$ 用等式 $\eqref{13} \eqref{15} \eqref{17}$ 的结果替换 $\Lambda$、 $\Gamma_{ij}^c$ 和 $\Gamma_{ij}^l$ 即可得出： $$ \begin{bmatrix} \bf m \newline 1 \end{bmatrix} \sim \begin{bmatrix} \alpha_{ij} R_{lc} \mathbf d_{ij}^c + \beta_{ij} \mathbf d_{ij}^l \newline -\beta_{ij} \mathbf b^\top \mathbf d_{ij}^l \end{bmatrix} \tag{19} \label{19} $$ 可以通过以下方法固定比例系数 $$ \beta_{ij} = -\frac{1}{\mathbf b^\top \mathbf d_{ij}^l} \tag{20} \label{20} $$ 将 $\eqref{20}$ 代回 $\eqref{19}$ 中，可以得到 $$ \mathbf m = -\frac1{\mathbf b^\top \mathbf d_{ij}^l} \mathbf d_{ij}^l + \alpha_{ij} R_{lc} \mathbf d_{ij}^c \tag{21} \label{21} $$ 式 $\eqref{21}$ 可以被改写成 $$ \alpha_{ij} \mathbf d_{ij}^c = R_{lc}^\top (\frac1{\mathbf b^\top \mathbf d_{ij}^l}\mathbf d_{ij}^l + \mathbf m) \tag{22} \label{22} $$

由于 $N = 3$ 对应的 $\mathbf n_i^c$ ， $\mathbf v_i^l$ 产生三个不同的方程，可以得到下面的系统： $$ \begin{cases} \alpha_{12} \mathbf d_{12}^c = R_{lc}^\top (Q_{12}^l + \mathbf m) \newline \alpha_{13} \mathbf d_{13}^c = R_{lc}^\top (Q_{13}^l + \mathbf m) \newline \alpha_{23} \mathbf d_{23}^c = R_{lc}^\top (Q_{23}^l + \mathbf m) \end{cases} \quad ; \qquad Q_{ij}^l = \frac1{\mathbf b^\top \mathbf d_{ij}^l} \mathbf d_{ij}^l \tag{23} \label{23} $$ 仔细分析可以发现，旋转 R 可以通过考虑两个众所周知的几何问题来求得：未知数 αij 可以作为标量深度来处理，以确定 perspective-3- pose (p3p) 问题的解； 并且，给定点对应的非齐次表示 $\alpha_{ij} \mathbf d_{ij}^c$、$Q_{ij}^l$，可以通过求解参考系之间的相对方向来计算旋转 $R_{lc}$ 和移位 $\mathbf m$ 。重新排列方程组 $\eqref{23}$ 以消除 $R_{lc}$ 和 $\mathbf m$ ，得到 $$ \begin{cases} \lVert \alpha_{12} \mathbf d_{12}^c - \alpha_{13} \mathbf d_{13}^c \rVert = \lVert Q_{12}^l - Q_{13}^l \rVert \newline \lVert \alpha_{12} \mathbf d_{12}^c - \alpha_{23} \mathbf d_{23}^c \rVert = \lVert Q_{12}^l - Q_{23}^l \rVert \newline \lVert \alpha_{13} \mathbf d_{13}^c - \alpha_{23} \mathbf d_{23}^c \rVert = \lVert Q_{13}^l - Q_{23}^l \rVert \end{cases} \tag{24} \label{24} $$ 在不失一般性的前提下，考虑向量 $\mathbf d_{ij}^c$ 具有单元范数（式 $\eqref{16}$ ）。应用余弦定律，我们就得到了 p3p 问题的经典方程： $$ \begin{cases} \alpha_{12}^2 + \alpha_{13}^2 - 2 \alpha_{12} \alpha_{13} \mathbf d_{12}^\top \mathbf d_{13} = \lVert Q_{12}^l - Q_{13}^l \rVert^2 \newline \alpha_{12}^2 + \alpha_{23}^2 - 2 \alpha_{12} \alpha_{23} \mathbf d_{12}^\top \mathbf d_{23} = \lVert Q_{12}^l - Q_{23}^l \rVert^2 \newline \alpha_{13}^2 + \alpha_{23}^2 - 2 \alpha_{13} \alpha_{23} \mathbf d_{13}^\top \mathbf d_{23} = \lVert Q_{13}^l - Q_{23}^l \rVert^2 \end{cases} \tag{25} \label{25} $$ 如 Fig. 3 所示，标量 $\alpha_{12}$、 $\alpha_{13}$ 和 $\alpha_{23}$ 被理解为未知深度值，可以通过 ⁶ 来求解。将深度值代入等式 $\eqref{23}$ 可生成一个方程组，该方程组涉及以不同参考系表示的 3 个点的非齐次坐标。这两个参照系之间的欧几里得变换 $R_{lc}$ 和移位 $\mathbf m$ 可以通过绝对定向算法直接计算出来。

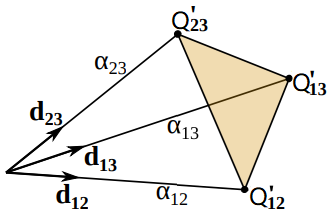
Fig. 3: 经典的 p3p 问题：给定点 $Q_{12}^l$、 $Q_{13}^l$ 和 $Q_{23}^l$ 之间的距离，以及向量 $\mathbf d_{12}$、 $\mathbf d_{13}$ 和 $\mathbf d_{23}$ 之间的夹角，求出未知深度 $\alpha_{12}$、 $\alpha_{13}$ 和 $\alpha_{23}$ 。

2.2.1.3 对于该求解方式的探讨

为了更好地理解方程组 $\eqref{23}$ 与将平面与共面线配准的原始问题有何关系。从方程 $\eqref{16}$ 可知， $\mathbf d_{ij}^c$ 是 $\Pi_i^c$ 和 $\Pi_j^c$ 法线的叉积，这意味着 $\mathbf d_{ij}^c$是两个平面相交线在相机坐标中的方向。另一方面， $\mathbf d_{ij}^l$ 是线 $L_i^l$ 和 $L_j^l$ 动量的叉积，即它对应于由原点 $O^l$ 和 $L_i^l$ 与 $L_j^l$ 交点所定义的直线的方向。从等式 $\eqref{12}$ 可以直接得出，方程 $\eqref{23}$ 中提供的 3 向量 $Q_{ij}^l$ 是线 $L_i^l$ 与 $L_j^l$ 的交点在激光坐标中的非齐次表示。最后，如 Fig. 2(b) 所示，向量 $\mathbf m$ 表示对偶空间中由 $\Pi_1^l$、 $\Pi_2^l$ 和 $\Pi_3^l$ 定义的平面的法线。 转换为 $\mathcal P^3$ 可知， $\mathbf m$ 是 3 个标定平面相交点在 2D 激光参考系中的非齐次表示。

由此可见，等式 $\eqref{23}$ 的 p3p 表述可以理解为对投影中心位于 $\mathbf m$ 的虚拟针孔摄像机的姿态进行估计，该摄像机观察由直线 $L_1^l$、 $L_2^l$ 和 $L_3^l$ 定义的三角形顶点（见 Fig. 4-b ）。请注意， $\mathbf m$ 的确定与平面线配准问题无关。因此，在使用 Grunert 算法找到标量深度后，只需求解旋转未知量的绝对方位，这意味着方程 $\eqref{23}$ 中的平移分量 $\mathbf m$ 并没有明确计算。众所周知，标准 p3p 问题最多有 4 个不同的实数解。不幸的是，方程 $\eqref{23}$ 中的标量未知数 $\alpha_{ij}$ 不具有深度的物理意义，允许取负值。因此，方程 $\eqref{25}$ 的 p3p 问题最多有 8 个不同的解，导致相同数量的相对旋转 $R$ 。

众所周知，只要出现以下情况之一，p3p 问题就会退化：（i）相机中心位于无穷远或与 3 个控制点位于同一平面； (ii) 摄像机中心位于包含 3 个控制点的圆柱体中，并且与它们定义的平面正交（危险圆柱体）。 在此问题中，只要一个棋盘平面平行于（或包含）其他两个平面相交的线（ Fig. 4-a ），就会出现第一种情况。 每当 3 个棋盘平面相交的点位于由 2D 激光重建的线的交点定义的危险圆柱体中时，就会出现第二种情况（ Fig. 4-b ）。

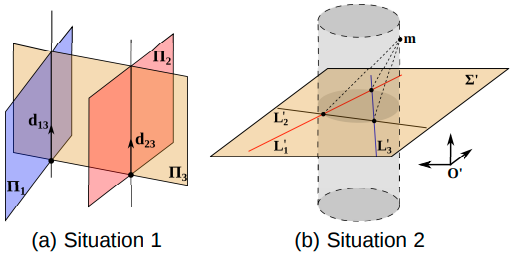
Fig. 4: 求解相对旋转 $R$ 时的奇异构型。情况 1：棋盘平面相交线平行。情况 2：3 个棋盘平面相交于一个点 m，该点位于由 2D 激光检测到的直线交点所定义的危险圆柱体。

2.2.2 位移变换

如 Fig. 2(a) 所示，对于每个可能的 $M$，对偶点 $\Pi_i^c$ 根据公式 $\eqref{10}$ 映射到 $\hat\Pi_i^c$ ，并通过连接 $\hat\Pi_i^c$ 和原点 $O^{c^* }$ 确定线 $W_i$。标定平面在 2D 激光参照系中的表示 $\Pi_i^l$ 由相应的线 $L_i^{l^*}$ 和 $W_i$ 相交确定。下一步是计算将 $\hat\Pi_i^c$ 映射到 $\Pi_i^l$ 的投影比例 $S$，并以唯一的方式定义两个传感器之间的相对平移 $\mathbf t_{lc}$ 。根据所述，我们首先替换方程 $\eqref{11}$ 中的 $\Pi_i^l$ 和 $\hat\Pi_i^c$ ，得出 $$ \mu_i \begin{bmatrix} \bf n_i^l \newline 1 \end{bmatrix} = \begin{bmatrix} I_{3\times3} & \mathbf 0_3 \newline -\mathbf t_{lc}^\top & 1 \end{bmatrix} \begin{bmatrix} R_{lc} \mathbf n_i^c \newline 1 \end{bmatrix} \tag{26} \label{26} $$ 其中，$\mathbf n_i^l$ 是平面 $\Pi_i^l$ 的法线，$\mu_i$ 表示未知的比例因子。考虑到前三个方程，可以得出 $$ \mu_i = \cfrac{\mathbf n_i^l {}^\top R_{lc} \mathbf n_i^c}{\mathbf n_i^l {}^\top \mathbf n_i^l} \tag{27} \label{27} $$ 并重新把 $\mu_i$ 代回式 $\eqref{26}$ 得 $$ \mathbf n_i^l {}^\top \mathbf n_i^l \mathbf n_i^c {}^\top R_{lc}^\top \mathbf t_{lc} - \mathbf n_i^l {}^\top \mathbf n_i^l + \mathbf n_i^l {}^\top R_{lc} \mathbf n_i^c = 0 \tag{28} \label{28} $$

因此，每个标定平面都会对矢量 $\mathbf t_{lc}$ 的条目产生线性约束，这意味着平移可以通过以下方法直接计算出来 $$ \begin{gather} \mathbf t = A^{-1} \mathbf b \newline A = \begin{bmatrix} \mathbf n_1^l {}^\top \mathbf n_1^l \mathbf n_1^l {}^\top \newline \mathbf n_2^l {}^\top \mathbf n_2^l \mathbf n_2^l {}^\top \newline \mathbf n_3^l {}^\top \mathbf n_3^l \mathbf n_3^l {}^\top \end{bmatrix} R_{lc}^\top \qquad \mathbf b = \begin{bmatrix} \mathbf n_1^l {}^\top \mathbf n_1^l - \mathbf n_1^l {}^\top R_{lc} \mathbf n_1^c \newline \mathbf n_2^l {}^\top \mathbf n_2^l - \mathbf n_2^l {}^\top R_{lc} \mathbf n_2^c \newline \mathbf n_3^l {}^\top \mathbf n_3^l - \mathbf n_3^l {}^\top R_{lc} \mathbf n_3^c \end{bmatrix} \end{gather} \tag{29} \label{29} $$ 总之，对于满足方程 $\eqref{23}$ 系统的每一种可能的旋转 $R$ ，都有一个相应的平移 $\mathbf t_{lc}$ ，可通过方程 $\eqref{29}$ 确定。

3. 3D 激光和相机外参数初始值求解

跟 2D 激光的单线数据仅仅能提供一条线相比， 3D 激光的多线数据能提供点云面的信息。因此，同样是利用激光点在标定板平面上这个约束，3D 激光的约束可以比 2D 激光更多一个。

3D 的激光的点云平面和标定板平面重合，意味着单帧 3D激光提供的有效约束为 3 个（即点云平面上的3个点落在标定板平面上），从而可以用 3 个激光点来构建公式 $\eqref{1}$ 的约束。这样两帧激光（6个约束）就能求解外参数了，求解方式可以利用前面 2D 激光所描述的方法（则同样存在 DLT 方法初始值不准的问题）。

这里给出了 3D 激光求解外参数的另一个思路，将单帧激光的点云平面和标定板平面重合的约束进行简单置换： $$ \begin{gather} R_{cl} \mathbf n^l = \mathbf n^c \newline \mathbf n^c {}^\top (R_{cl} P^l + \mathbf t_{cl}) + d^c = 0 \end{gather} \tag{30} \label{30} $$ 公式 $\eqref{30}$ 中的两个方程中，第一个方程能提供 2 个有效约束，第二个方程提供 1 个有效约束。虽然公式 $\eqref{30}$ 中和三个点落在平面上的物理意义一样，但是，公式 $\eqref{30}$ 中第一个方程只和旋转矩阵有关，和平移无关。意味着可以先求解旋转矩阵，再线性求解平移向量，从而简化参数估计。

当激光帧数 N 大于等于 2 时，可以求解如下非线性最小二乘问题来计算旋转矩阵： $$ C = \sum_{i=1}^N \lVert \mathbf n^c - R_{cl} \mathbf n^l \rVert^2 \tag{31} \label{31} $$ 求解参考 ^{1 7}介绍上述问题的通用解法。

4. 基于平面约束的优化

通过上述方式计算出外参数的初始值之后，再对采集的 $N$ 组数据进行联合优化得到最优估计，假设第 $i$ 帧激光有 $N_i$ 个激光点落在标定板上，同时第 $i$ 帧激光对应的标定板平面方程在相机坐标系的表示为$[\mathbf n_i^c, d_i^c]^\top$：

$$ \hat R _{cl}, \hat{\mathbf t} _{cl} = \underset{R _{cl}, \mathbf t _{cl}}{\arg \min} \sum _{m=1}^N \frac1{N_i} \sum _{i=1}^{N_i} \lVert \mathbf n_i^c {}^\top (R _{cl} P _{im}^l + \mathbf t _{cl}) + d^c \rVert^2 \tag{32} \label{32} $$

5. 其他方式的相机激光雷达标定

参考文献 ^{8 9 10 11 12 13} 。

Reference