ELSED: 增强型线段绘制

ELSED: Enhanced Line SEgment Drawing

检测数字图像中的线段和完整线条是计算机视觉（CV）中经常出现的一个问题。线段在理解场景的几何内容方面发挥着重要作用，因为它们是图像内容的压缩和有意义的表示。此外，线段仍然存在于低纹理的环境中，而基于角点或斑点的经典方法在这些环境下通常会检测失败。线段检测已用于大量 CV 任务，例如三维重建、SLAM、视觉里程计、通过消失点检测的三维相机定位、飞机上的电缆检测，或合成孔径雷达图像中的道路检测。

如今 CV 算法无处不在，它们有望在资源有限的设备上运行。 为此，诸如局部特征检测器这样的低级算法必须非常高效。传统的基于霍夫变换 (Hough transform) 的全局线检测方法效率低下。 因此，出现了各种解决效率问题的局部方法。LSD 是最早以局部方法取得优异结果的方法之一。边缘绘制方法进一步提高了效率。在第一步中，它们的工作方式是沿着与梯度垂直的方向连接边缘像素。在第二步中，他们将所需的曲线（最简单的情况下是一条线）与这些边缘拟合。

文献 ¹ 提出的方法通过对连接的边缘像素进行线段拟合并使用其方向来指导绘图过程，从而改进了绘图方法。将绘图和线段拟合融合在一个步骤中，节省了时间，并提高了检测到的线段的整体质量。此外，作者的方案允许跳过梯度不连续的地方，检测完整的整条线段，或者只检测单个线段而不跳过。这一点很重要，因为线段是在梯度层面上的特征，很容易被遮挡、阴影、突发事件等破坏。通过这种方式，用户可以定义最适合应用程序的线段类型。 例如，如果目标是进行消失点估计或用于重建和匹配的较短片段，我们可能会选择检测大片段。

在本文中，我们提出了一种高效的线段检测方法，即增强型线段绘制 (Enhanced Line SEgment Drawing, ELSED)¹ 。作者在实验中，将 ELSED 的准确性和效率与其他近期的检测器进行了比较。如 Fig. 1 所示，ELSED 不仅是最有效的（注意速度维度的对数尺度），而且在线段检测中也是最准确的，并且可重复性更高，它提高了资源有限设备中现有方法的效率，为在任何类型的硬件上运行的新 CV 应用程序打开了大门。

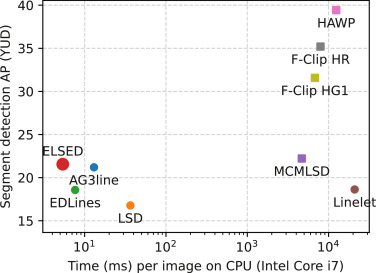
Fig. 1: 线段检测问题中的平均精度 (Average Precision, AP) 与执行时间 (ms) 曲线。 基于局部特征的方法用圆形标记显示，全局方法用方形标记显示。

目前，线段检测的方法可以将其分为四大类 ²³：1) 基于全局霍夫变换方法的检测器、2) 贪婪检测局部特征的线段检测器 (又可以细分: a. 基于局部梯度统计; b. 基于局部边缘拟合) 、3) 基于神经网络的线段检测器 (又可以细分: a. 线段检测 [Line segment approach] ; b. 线框检测 [Wireframe approach]) 、4) 基于混合方式的线段检测器。每种方式都有各自的优缺点。ELSED 是基于局部边缘拟合的线段检测器，下文对其算法进行详细的展开。

1. 增强型边缘绘制算法 - Enhanced Edge Drawing algorithm (EED)

EED 需要以下高级步骤： 1) 高斯平滑以抑制噪声； 2) 梯度大小和方向计算； 3) 提取锚点像素，梯度幅值的局部最大值； 4）使用增强路径算法连接锚点。对于降噪步骤，使用 $5 \times 5$ 大小标准差 $\sigma = 1$ 的高斯内核对图形进行卷积。对于梯度大小和方向计算，首先通过应用 Sobel 算子计算水平梯度 $G_x$ 和垂直梯度 $G_y$ ，然后使用 $L1$ 范数作为幅值 $G = |G_x| + |G_y|$ 。设定一个梯度阈值，对低于该阈值的像素设置 $G=0$ ，并将梯度方向 $O$ 量化为两个可能的值：垂直边缘 $|G_x| \geq |G_y|$ ，或水平边缘 $|G_x|<|G_y|$ 。

1.1 锚点像素的提取 - Extraction of anchor pixels

锚点是绘制过程开始的像素。扫描 $G>0$ 的图像像素，并测试它是否是梯度幅值 $G$ 中沿梯度量化方向 $O$ 的局部最大值。如果像素方向 $O(x, y)$ 对应于垂直边缘有 $G[x,y] - G[x-1,y] \geq T_{anchor}$ 且 $G[x,y]-G[x+1,y] \geq T_{anchor}$ 则为锚点。同理，适用于垂直方向的水平边缘。为了提高处理速度，可以通过增加 $T_{anchor}$ 的值来限制锚的数量，也可以通过每 $SI=2$ 列和行扫描像素来限制。

1.2 通过增强路径算法连接锚点 - Connecting the anchors by an enhanced routing algorithm

边缘绘制 (Edge Drawing, ED ⁴) 比 LSD 的区域增长更快，因为从最初的锚点开始，它只沿着边缘像素链行走，在每一步评估 3 个邻居（见 Fig. 2-(a)）并选择具有最大梯度幅度的作为下一步。 这些评估对于算法的速度至关重要，因为它们是针对从锚点出发的每个可到达的边缘像素进行的。

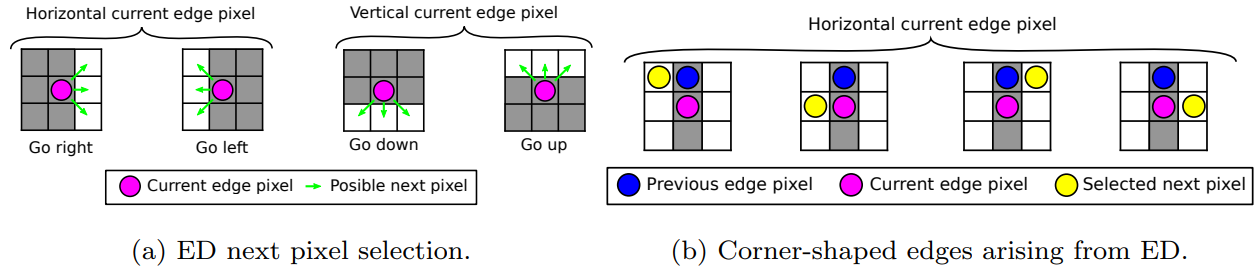
Fig. 2: ED贪婪段增长。在 (a) 中，它只考虑当前边缘像素。在 (b) 的情况下，行走是从蓝色像素开始的，并找到一个水平的边缘像素（粉红色的）。因此，它将开始向左和向右行走，这可以产生具有显示配置的边缘链（蓝-粉-黄像素序列）。

在 EED 程序中，同时进行边缘绘制和线条拟合。这能够通过减少检查像素的数量来节省计算量。在绘制过程中，考虑前一个和当前一个像素。在行走过程中，只要边缘方向没有从上一个像素变为当前像素，我们就会探索与 ED 相同的像素（见 Fig. 3-(b) 中的 “Go right”, “Go left”, “Go up” and “Go down”）。当前一个像素处于垂直边缘，而当前像素处于水平边缘时，ED 有 6 个候选像素要加入到当前线段中（见 Fig. 3-(a) ）。这可能会产生这样的情况，即算法会画一个角，打破线的假设（见 Fig. 2-(b)）。同样的情况也发生在前一个像素处于水平边缘而当前像素位于垂直边缘的情况下。

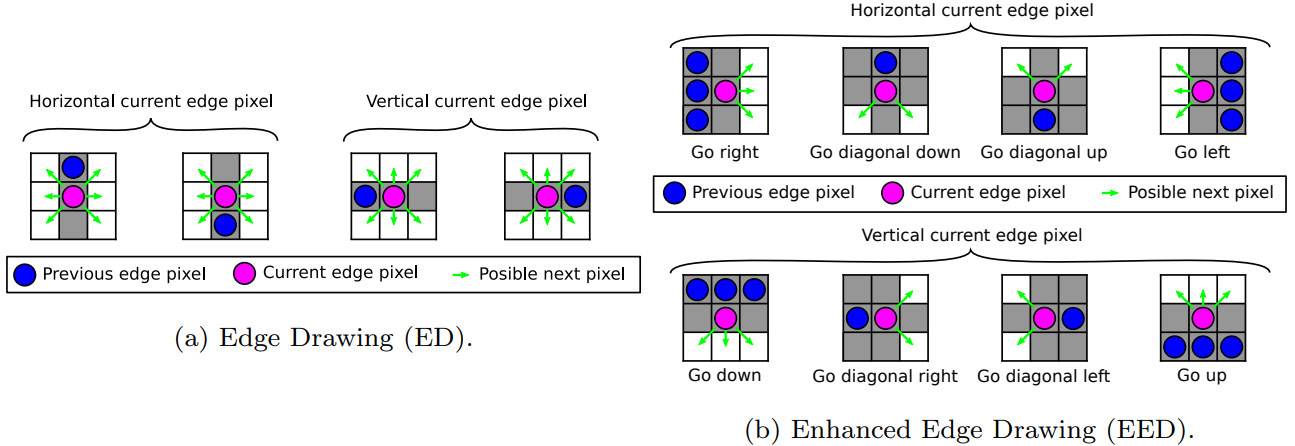
Fig. 3: 绘制对角线的边缘：当前一个像素的方向（垂直与水平）与当前像素不同时，原始 ED 有 6 个候选像素，而 EED 有 3 个或 2 个。当有相同的前一个像素选项的候选像素时，会显示一个以上的前一个边缘像素。

在这里，我们引入了一种不同的方法来处理这些对角线像素，同时跟随一条线。增加一个假设，即边缘链应该形成一条线。然后，考虑到 Bresenham 的线图方案，在这种情况下，检查的像素数量从 ED 的 6 个（见 Fig. 3-(a) ）变为 EED 的只有 2 个（见 Fig. 3-(b) 中的四个 “对角线 “情况），而对于其他可能的前一个像素（非对角线情况）则保持3个。这有两个优点： 1）它比原来的 ED 路径化算法更快，因为它探索的像素更少；2）它避免了寻找线段的非意义情况。

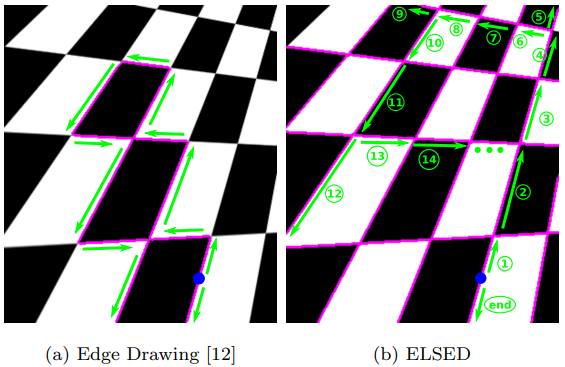
Fig. 4: 从一个单一的锚点（蓝点）开始的 ED 和 EED 的绘制过程的结果（紫色像素）。绿色箭头和数字确定了哪些区段首先被访问。

第二个重要的想法也是试图寻找对齐的边缘像素的结果。当检测到边缘方向发生变化时，ED 会改变行走过程的方向（见 Fig. 4-(a)），而 EED 则试图沿着一条线继续沿同一方向前进。 然而，边缘方向的任何变化都不会被遗忘，并且会被推入不连续点堆栈 $D_{stack}$ 以供以后处理（参见 Alg. 1）。如果链接了超过 $T_{minLength}$ 个像素并且像素对齐的平方误差低于 $T_{LineFitErr}$，EED 就会尝试将一条线拟合到当前的像素链上。线段段搜索的最后一个参数是 $T_{PxT oSegDist}$，它是考虑像素是否属于当前段的最大距离（以像素为单位）。这是在 Alg. 1 第 15 行的函数 addPxToSegment 内部完成的。当没有更多的像素可以链接时（即在图像的极限，只有已经访问过的像素或弱边缘像素作为候选）或检测到线边缘不连续（例如，两个对齐窗口之间的间隙，树枝 遮挡建筑物的一部分等）。 如果检测到不连续性，将按顺序执行以下操作：

1. 如果沿着一条线段行走（即已经拟合了一条线），则尝试沿线方向延伸它（行走过程使用 Alg. 1 中的 canContinueForward 和 forwardPxAndDir 函数叠加，第 23 行至 26 行）
2. 如果沿着一条线段行走，并且不能继续前进，则尝试向后延伸该线段（行走过程使用 Alg. 1 中的 canContinueBackward 和 backwardPxAndDir 函数叠加，第 27 行至 30 行）
3. 沿着梯度方向继续前进，也就是在不连续的地方改变（ Alg. 1 中堆积的行走过程，第 22 行）

Alg. 1: 增强型边缘绘制算法 - Enhanced Edge Drawing algorithm (EED)

这种有序的行动序列保证了如果检测到一条线段，它的所有像素将被一起检测。在 Fig. 4-(b) 中展示了一个说明性示例，EED 启动了两个行走过程，一个向上走，另一个向下走。与 ED（见 Fig. 4-(a)）不同，EED 检测到棋盘角的边缘方向的不连续性，并继续沿着当前的线方向行走。每个不连续点都被储存在 $D_{stack}$ 中，以便以后处理。在片段 (1) 到 (5) 中的像素被链起来之后，要处理的下一个边缘方向从 $D_{stack}$ 的顶部提取。绘制过程从它开始不断绘制，将 (6) 到 (9) 段的像素连接起来。当 $D_{stack}$ 中没有更多的边缘方向变化时，路径化算法结束。然后，下一个锚点被路径化算法处理。从一个锚点检测更多的线段是该方法的一个重要特征，它增加了与 EDLines⁵ 相比的检测召回率。

2. 线段的不连续性 - The line segment discontinuities

一条线段可以被多个边缘不连续点打断。这些是梯度方向发生变化或梯度幅度变为零的图像区域。无论目标是检测整条线还是仅仅检测线段，不同长度的不连续点（即没有边缘或边缘方向与线段不一致的像素数）在绘制过程中应该被正确跳过，以便正确检测线段。

Alg. 1 自然地处理了这种现象。一旦检测到不连续，算法的目标是跳过它并尽可能在线段方向继续绘制。先验的，不连续长度是未知的，该算法测试不同长度的候选者。由于使用了 $5 \times 5$ 高斯平滑核，任何 1 像素的不连续都会在至少 5 像素的邻域产生影响，因此将不连续的最小长度设定为 5 像素。在函数 canContinueFordward（ Alg. 1 第 23 行）和 canContinueBackward（ Alg. 1 第 27 行）中，检查了不同的跳跃长度 $J$（在算法的默认参数中，使用 $J \in [5, 7,9]$ ）。如果以下条件的有序结合为真，那么绘制过程将在出现不连续后继续：

1. 该段长于要跳过的像素数 $J$
2. 与片段对齐的像素 $a$ 和远离当前像素 $c$ 有 $J$ 个像素，在图像内且 $G[a]>0$（即不是一个弱边缘像素）
3. 从 $a$ 开始，EED 至少可以沿着边缘方向绘制 $J$ 个像素点。 称这组 $J$ 像素为扩展像素
4. 延伸像素与线段对齐良好。为了检查这一点，计算了一个小邻域中图像梯度的自相关矩阵 $M$ （在延伸像素的每一侧取一个像素）然后进行断言：$\cfrac{\lambda_1}{\lambda_2} \geq T_{EigenExt}$ ，其中 $\lambda_1 ,\lambda_2 (\lambda_1 > \lambda_2)$ 是 $M$ 的特征值且 $\angle({\bf v} _1 ,{\bf n}) \leq T _{AngleExt}$ ，其中 $\angle(\cdot, \cdot)$ 是角距离，${\bf v}_1$ 是 $M$ 的第一个特征向量，$\bf n$ 是该段的法线向量。

在 Fig. 5 中，展示了合成图像中不连续管理算法的不同步骤。在 Fig. 5-(d) 中展示了从图像左侧开始的检测过程，将边缘像素（蓝色）与水平线（绿色）相匹配。当边缘方向从水平方向变为垂直方向时，将最后一个边缘像素检测为异常值（橙色），因此该算法的方法检测到处于不连续状态中。在这种情况下，红色像素是 $|E|>T_{ol}$ 时检测到的最后一个像素，其中 $T_{ol}$ 是异常值的最大数量。

接下来的 Fig. 5-(e) 显示了为决定是否应该继续画直线或线段已经完成而进行的检查。紫色像素是处于不连续状态的像素，在当前线段方向使用 Bresenham 算法绘制时会跳过。 红色像素是沿着边缘方向（绿色）绘制的，从不连续点 $a$ 之后的第一个像素开始。还用红色标记了用来计算 $M$ 的特征值验证区域的邻居像素，如果 canContinueForward 函数中的扩展像素可以继续前进。此合成示例中的像素没有统一的梯度方向，因此，该过程会丢弃所有使用长度 $J \in [5, 7,9]$ 测试的扩展。因此，该算法关闭了第一线段并继续在主要梯度方向向上绘制。 当收集到足够的像素时，会拟合另一个线片段（ Fig. 5-(f) ）。当到达图像的顶部时，该段被向后方向向下延伸。当这种情况发生时，管理不连续的机制再次被激活，如 Fig. 5-(g) 所示，但这次该区域满足所有定义的标准，因此执行了跳跃。 Fig. 5-(h/i) 分别显示了拟合的边缘和直线片段。局部分段检测方法的局限性之一是产生了许多由梯度不连续产生的小段。上述过程可以帮助缓解这种情况。

Fig. 5: ELSED 不连续性管理算法示例。 (c) 中的梯度方向用红色（向右）、紫色（向上）、青色（向左）和浅绿色（向下）编码。

3. 验证生成的候选直线段 - Validation of the generated segment candidates

在 EED 之后，在检测出来的线段中可能存在错误（见 Fig. 6 的红色线段）。它们主要发生在具有高密度边缘像素的区域。 为了验证一条线，使用线段像素的梯度方向，将其方向与线段的法线方向进行比较，即角度误差。这种验证可以有效地进行，而不会损害整体性能。

Fig. 6: ELSED 检测到的“真”直线（绿色）和“假”直线（红色）段。 通过比较 YorkUrban-LineSegment 数据集（蓝色）的 ground truth 段与未经验证的 ELSED 检测（洋红色）进行比较得到这些标签

为了进行良好的验证，丢弃了位于不连续点和端点附近的像素，因为即使在正确的检测中，它们通常也具有不同的梯度方向。尽管如此，真实片段中的梯度方向误差是一个嘈杂的信号。 在 Fig. 7 中，可以看到真实直线区段检测（TP）（蓝色）、假直线区段（FP）（橙色）和随机噪声强度图像中检测到的假直线区段（绿色）上的像素方向误差的概率分布函数（PDF）。很明显，TP 段上的像素比 FP 段上的像素的角度误差小。但是，FP 和 TP 分布之间存在明显的重叠。因此，使用了一个对噪声稳健的验证标准。如果一个区段至少有 $50 %$ 的像素的角度误差低于阈值 $T_{valid}$，将之验证一个直线片段。为了将积极的检测（即有效的检测）与消极的检测区分开来，学习了一个阈值 $T_{valid}=0.15$ 弧度，它可以保持较高的召回率，放弃少数真正的检测。

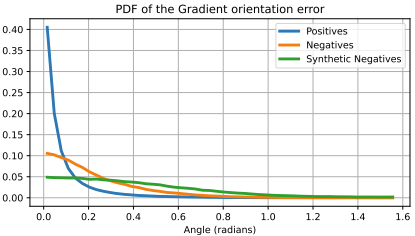
Fig. 7: 正确片段（蓝色）、消极片段（橙色）和随机强度图像中检测到的片段（绿色）的梯度方向误差的 PDF

4. 参数选择 - Parameter selection

ELSED 算法的实现在 iago-suarez/ELSED 。大多数 ELSED 参数已根据经验设置，用户无需更改。 使用高斯平滑滤波器（$\sigma=1$，内核大小 $=5\times5$），梯度阈值$T_{grad}=30$ ，锚点阈值 $T_{anchor}=8，SI=2$，定义了锚点每隔 $SI$ 行/列的扫描间隔。对于线段拟合：$T_{ol} = 3，T_{minLength} = 15，T_{LineF itErr} = 0.2，T_{PxToSegDist} = 1.5$ ，和用于验证的 $T_{EigenExt} = 10，T_{AngleExt} = 10^\circ，T_{valid} = 0.15$ 弧度。

然而，其他参数可以由用户调整，以定义要检测的段的类型；在不连续管理中要检测的跳跃长度列表就是这种情况。由于这与第一步中高斯平滑核的大小（在实现中为 $5\times5$ ）和梯度卷积核的大小（在例子中为 $3\times3$ ）直接相关，因此定义了一组默认值 $(5,7,9)$，在实验中取得了良好的结果。

Reference