高效的自适应非极大值抑制

Efficient adaptive non-maximal suppression

关键点检测通常是各种任务的第一步，如 SLAM、全景图拼接、相机标定和视觉跟踪。因此，这个阶段可能会影响到上述应用的鲁棒性、稳定性和准确性。在过去的十年中，我们见证了关键点检测器的重大进展，导致在准确性、速度和可重复性方面的重大改进。但是，虽然对关键点的检测进行了深入的研究，但对确保其均匀的空间分布的关注程度却相当低。众所周知，空间点的分布对于避免像 Fig. 1 中描述的结构退化（针对于 SFM 或 SLAM）或冗余信息（例如，点群）这样的问题情况至关重要。此外，均匀且非簇状的点分布可能会加快大多数计算机视觉 pipelines 的速度，因为覆盖整个图像所需的关键点数量较少。确保良好分布的关键点检测的最有效解决方案之一是对检测器提取的关键点应用自适应非最大抑制（ANMS）算法。然而，尽管这些方法有很多优点，但由于其高计算复杂性，这些方法在实践中很少被使用。为了克服这一局限性，文章¹中提出了三种新的方法，即 Range Tree ANMS (RT ANMS)、K-d tree ANMS (K-dT ANMS) 和通过方形覆盖抑制（Suppression via Square Covering, SSC）。所开发的算法旨在有效地选择整个图像中最强和分布良好的关键点。我们使用以最佳和直观的方式初始化方形搜索范围近似来实现这样的性能（见 Fig. 2 ）。作者通过大量的实验在速度、空间分布和内存效率方面以及应用于 SLAM 上后的性能表现证明所提出的算法高效且有用，并提供了代码 BAILOOL/ANMS-Codes 。

Fig. 1: 关键点检测：(a) TopM NMS，(b) Bucketing，(c) Efficient ANMS。右下角的子图像表示使用高斯核计算的关键点的覆盖率和集群性。子图像中的红色代表密集的点群，而蓝色代表未覆盖的区域。

1. 桶状方法 - Bucketing approach

目前，基于 bucketing 的点检测方法是最常用的技术，用于确保关键点的良好再分配。这种方法相对简单：将源图像划分为一个个网格，在每个网格单元中检测关键点（亦或是相似的变形，来源于 ORB-SLAM 中利用四叉图结构将关键点进行离散均匀化）。基于桶的方法对于检测整个图像的关键点是有效的，然而，它无法避免冗余信息的存在（例如关键点的集群）。

2. 非极大值抑制 - Non-maximal suppression

NMS（也被称为 TopM ）经常被用来去除大量的关键点，这些关键点大多是冗余的或者是关键点检测器的噪音反应。最常见的 NMS 方法：使用经验确定的阈值来抑制较弱的关键点，然后通常通过抑制不属于特定半径的局部最大值的关键点来减少集群性。NMS 是一种直接和快速的方法来拒绝不必要的角落，但是，在许多实际情况下，这种方法导致关键点的空间传播非常有限（见 Fig. 1-(a) ）。

3. 自适应非极大值抑制 - Adaptive non-maximal suppression

为了解决上述缺点，M. Brown² 出了自适应非极大值抑制算法，实现了特征点在局部上的稀疏分布和全局上的均匀分布。自适应非极大值抑制算法基本思想是评估所有候选点的极大区域，并进行排序。具体来说，就是对所有点 $N$ 寻找它的响应 $f({\bf x}_i)$ 能作为区域最大值的最小区域半径 $r_i$

$$ r_i = \min_j \lVert {\bf x}_i - {\bf x}_j \rVert \quad {\rm s.t.} \ f({\bf x}_i) < c _{\rm robust} f({\bf x}_j) \quad {\bf x} _{i/j} \in \mathcal I \tag{1} \label{1} $$

其中 $i/j \in [0,1,\cdots,N-1]$ ，${\bf x}_i$ 表示候选点坐标，$\mathcal I$ 是所有候选点的集合。使用 $c _{\rm robust} = 0.9$ 的值，这可以确保一个邻居必须有明显更高的强度才能发生抑制。不幸的是，这种 ANMS 的原始实现具有二次复杂性，不适合于 SLAM 等实时应用。

double computeR(cv::Point2i x1, cv::Point2i x2) {
  return norm(x1 - x2);
}
template <typename T>
std::vector< size_t> sortIndexes(const std::vector< T>  & v) {
  // initialize original index locations
  std::vector< size_t>  idx(v.size());
  for (size_t i = 0; i != idx.size(); ++i) idx[i] = i;

  // sort indexes based on comparing values in v
  sort(idx.begin(), idx.end(),
       [&v](size_t i1, size_t i2) {return v[i1] >  v[i2]; });

  return idx;
}

std::vector<cv::KeyPoint> ANMS(const std::vector<cv::KeyPoint>& kpts,int num = 500) {
  int sz = kpts.size();
  double maxmum = 0;
  std::vector<double> roblocalmax(kpts.size());
  std::vector<double> raduis(kpts.size(), INFINITY);
  for (size_t i = 0; i < sz; i++) {
    auto rp = kpts[i].response;
    if (rp > maxmum)
      maxmum = rp;
    roblocalmax[i] = rp*0.9;
  }
  auto max_response = maxmum*0.9;
  for (size_t i = 0; i < sz; i++) {
    double rep = kpts[i].response;
    cv::Point2i p = kpts[i].pt;
    auto& rd = raduis[i];
    if (rep>max_response) {
      rd = INFINITY;
    } else {
      for (size_t j = 0; j < sz; j++) {
        if (roblocalmax[j] > rep) {
          auto d = computeR(kpts[j].pt, p);
          if (rd > d)
            rd = d;
        }
      }
    }
  }
  auto sorted = sortIndexes(raduis);
  std::vector<cv::KeyPoint> rpts;

  for (size_t i = 0; i < num; i++) {
    rpts.push_back(kpts[sorted[i]]);
  }
  return std::move(rpts);
}

4. 基于树状数据结构的自适应非极大值抑制 - ANMS based on tree data structure

为了决绝实时性问题，作者提出了依赖于保持良好空间关键点分布的树状数据结构 (Tree Data Structure, TDS) 的 ANMS。K-dimensional Tree (K-dT) 和 Range Tree (RT) 被用于此目的。首先，K-dT 是一个二进制搜索树，其中每个节点的数据是空间中的一个 K 维点。使用这种数据结构可以进行空间分区，以组织 K 维空间中的点。这种分区可以用来有效地检索属于某个特定点周围的定义范围的点集 ${\bf P}_w$ 。另一方面，RT 是 K-dT 的一个替代方案，与 K-dT 相比，RT 通过更为复制的存储结构来换取更快的查询时间。虽然这两种数据结构本质上是不同的，但从高层的角度来看，该算法是通用的，适合于任何能够检索定义范围内的点集的数据结构。

按强度降序排列（即角点得分）对关键点 $P_{in}$ 建立 TDS 。 以便在给定搜索范围的情况下有效地获取特定关键点的最近邻居的方法。 该搜索范围由二分搜索确定，二分搜索试图猜测最合适的搜索范围 $w$ 以满足查询的关键点数量。 对于每个 $w$ 猜测，每个关键点的最近邻居（按强度降序处理）被抑制，这样它们将不会在所选 $w$ 下的进一步迭代中被考虑。 为此，索引列表 ${\bf Idx}_s$ 用于跟踪被抑制的关键点。 根据公差阈值 $m \pm t$，当检索到的关键点数接近查询的关键点数 $m$ 时，二分搜索终止。算法流程如下（搜索范围 $w$ 的初始值由 6 小节 提供）：

比较了 K-dT ANMS 和 RT ANMS，观察到它们在关键点重复性和集群性方面有相似的表现。值得一提的是，在 K-dT 的情况下，搜索范围是由候选点周围的半径定义的，而 RT 使用的是搜索范围的平方近似值。这种平方近似可以潜在地提高 ANMS 的速度性能。

5. 通过方形覆盖抑制 - Suppression via Square Covering

构建树状数据结构会随着数据的增大而增大耗时，因此，作者通过在关键点上叠加一个网格 $G_w$ 来模拟一个近似的半径-近邻查询。一旦设置了网格 $G_w$ ，就会尝试覆盖位于 $2w$ 范围内的单元格，而不管这些点在这个方形覆盖范围内的确切位置。 这极大地提高了算法的性能，因为单元格的覆盖仅通过遍历方形搜索范围来执行，而不需要欧几里得距离计算。算法的图示过程如下：

(a) 原始图像中的关键点检测（以蓝色表示），(b) 按搜索范围的强度和初始化对关键点进行排序，(c) 我们的 ANMS 算法的概念表示，其中：每一列代表搜索范围猜测 （橙色框）通过二分制搜索过程迭代，直到达到查询的点数（本例中为 100）； 虽然每一行都描述了通过输入点的迭代，(d) 最终结果，其中红点代表选定的关键点。

算法的伪代码如下（搜索范围 $w$ 的初始值由 6 小节 提供）：

6. 搜索范围的初始化 - Initialization of search range

在第 4、5 小节中使用二分法搜索来猜测适当的搜索范围。如果假设二分法起初的上界限 $a_h$ 为图像宽度 $W_I$ ，下界限 $a_l$ 为 $1$ 的话，往往会导致不必要的迭代并降低收敛速度。为此，作者设计了一个制定初始边界的算法。

根据需求，希望的是在图像上均匀地分布 $m$ 个被检测的点，而且没有任何集群。 为此，我们尝试用边长为 $2a_h$ 的正方形覆盖图像，正方形中心之间的距离最小为 $a_h + 1$（见下图）。

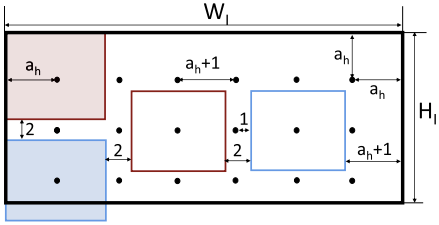
最佳点分布的图形表示，不同颜色的边框代表候选点周围的搜索范围

给定 $a_h$ 和 $W_I$ ，可以计算出完全适合一行图像的正方形的最大数量。 把这个行定义为一组放置在图像中相同高度的方块，其中一行的第一个和最后一个方块与图像边界完全对齐。如果每行里面有 $q$ 个点（即正方形中心），那么每行中这些点之间有 $q-1$ 个距离。此外，左边和右边的极端点位于与图像的左右边界的 $a_h$ 处。因此，我们可以用 $a_h$ 和 $q$ 来表示图像宽度 $W_I$ ： $$ W_I = 2 a_h + (a_h + 1) (q - 1) \tag{2} \label{2} $$ 因此，根据式 $\eqref{2}$ 可以得到每行里面的点数： $$ q = \frac{W_I - a_h + 1}{a_h +1} \tag{3} \label{3} $$ 类似地，可能适合图像高度 $H_I$ 的正方形中心 $l$ 的最大数量为： $$ H_I = 2 a_h + (a_h + 1) (l - 1) \tag{4} \label{4} $$ 期望检测的点数 $m$ 等于 $q$ 和 $l$ 的乘积。通过将 $l = m/q$ 代入方程式 $\eqref{4}$ ，并从公式 $\eqref{4}$ 代入 $q$ ，得： $$ (m-1) a_h^2 + a_h(W_I + 2m + H_I) + m + W_I - H_I W_I = 0 \tag{5} \label{5} $$ 求解这个等式 $a_h$ 会产生两个解，其中一个总是负数，而另一个则给我们提供了正方形边的最终估计： $$ \begin{align*} a_h &= - \frac{H_I + W_I + 2m - \sqrt \Delta}{2(m - 1)} \newline \Delta &= 4W_I + 4m + 4H_Im + H_I^2 + W_I^2 - 2W_I H_I + 4 W_I H_I m \end{align*} \tag{6} \label{6} $$ 虽然该方案试图分配尽可能多的点，但它并不保证图像上的点的数量将完全等于 $m$ 。可以通过最差的点分布来确定二分法搜索的下界限 $a_l$ 。 当所有的 $n$ 个输入点都位于图像上的一个正方形中，并且它们之间没有空间时，就会发生这种情况。考虑到这样的分布，希望通过用边长为 $2a_l$ 的最小的正方形填充这个空间来检索出至少 $m$ 个被查询的点。这在数学上可以表示为 $m(2a_l)^2=n$ 。因此，二元搜索的下限公式如下： $$ a_l = \frac12 \sqrt{\frac nm} \tag{7} \label{7} $$

Reference