边缘绘制: 一个兼具实时性的边缘段检测器

Edge Drawing: A combined real-time edge and segment detector

边缘检测是一个非常基本和重要的问题，是许多计算机视觉和模式识别应用程序中流行的第一步。高质量的边缘图，被定义为由完美连续的、定位良好的、无抖动的和一个像素宽的边缘段组成，可以显著提高计算机视觉和模式识别应用的其余部分的性能 ; 然而，低质量的边缘图（连接性差、边缘宽度变化、错误的分支和缺口等）会严重影响应用程序其余部分的成功。

在传统的边缘检测算法中，检测边缘的一个通用方法是对图像应用一系列的过滤器。 第一步通常是让图像通过低通滤波器，以减少噪声并平滑图像。由于边缘是图像的高频分量，因此应用高通滤波器（导数或梯度算子，例如 Prewitt、Sobel 和 Feldman、Scharr等）来提取区域边缘所在的位置。梯度算子的输出被称为梯度图，它通常被阈值化以抑制图像的低频、非边缘区域。经过梯度阈值处理的像素构成了所谓的边缘区域，它由几个像素宽的图像厚条组成 (见 Fig. 3-(a)) 。最后的任务是对边缘区域的剩余像素进行处理，获得薄的、连续的、无抖动的和定位良好的边缘。这是边缘检测中最重要和最困难的一步，可以通过镂空化 (skeletonization) 、非极大值抑制、边缘细化或形态学算子的应用等技术来实现。但是，这些技术以孤立和单独的方式评估边缘区域的每个像素，使其成为潜在的边缘元素 (edge element, edgel) ，如果它（在预先设定的阈值梯度大小中）高于其邻居沿同一梯度方向的梯度值，则该像素被标记为边缘元素。这种短视的局部推理导致了低质量的边缘图。（见 Fig. 1 ，它显示了由 OpenCV Canny 算法生成的著名 Lena 图像的边缘图，其中一些低质量的边缘斑块已突出显示）

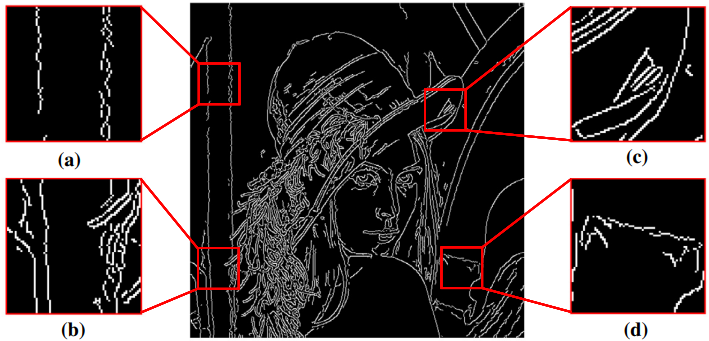
Fig. 1: 在中间 —— Lena 的边缘图由 OpenCV Canny (low threshold: 30, high threshold: 60, aperture: 3) 得到。Lena 图像首先由 $\sigma = 1$ 的 $5\times5$ 高斯核平滑。 (a) 由噪声引起的缺口实例和不连续性，(b) 未被关注的边缘形成，(c) Lena 帽子边界上两像素宽的边缘段，(d) 具有不连续性的不光滑边缘段。

文献¹² 提出了一种边缘段检测算法，提出的算法模仿了在点对点的边界完成拼图中通过绘制一个边缘段来连接连续的点的想法 (见 Fig. 2-(a)) ，通过计算一组代表给定图像强度变化的稳定地标的点（称为锚点），然后使用一个智能路径算法来连接连续的锚点。所提出的算法是在连续的锚点之间绘制一个边缘段，因此被称为边缘绘制 (Edge Drawing, ED) 。文献中贡献的最重要部分，不应该与传统边缘连接范式混为一谈，后者是将已经计算好的边缘图作为输入，并在边缘质量指标方面进行改进。因为 ED 从一开始就通过计算少量的点来检测边缘，所以不需要后期处理方法就可以得到高质量的边缘。此外，ED 能够以向量形式输出结果，作为链式检测边缘段的数组。

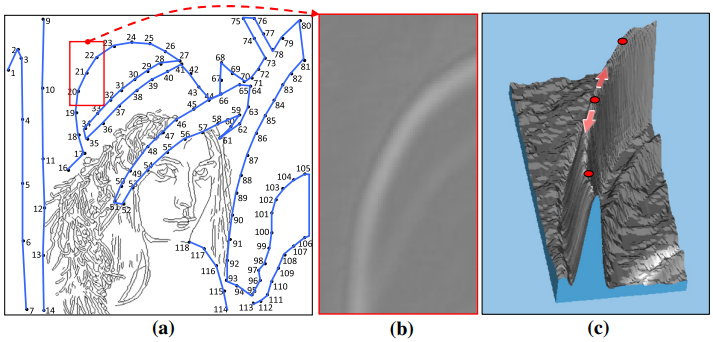
Fig. 2: (a) Lena 的边缘图计算问题被表述为一个点到点的边界完成难题。当连续的点被连接起来时，可以得到一个由干净的、一像素宽的、连续的边缘段组成高质量的边缘图。(b) Lenas 帽子的梯度图中的一个区块。(c) 为 (b) 中区块的三维图，两个锚点样本用红色标记，箭头表示锚点的连接方向。

1. 边缘绘制算法 - Edge Drawing algorithm

ED 算法实现在灰度图像上，由四个主要步骤组成：

1. 通过高斯滤波抑制噪声
2. 计算梯度大小和边缘方向图
3. 锚点的提取
4. 通过智能路径连接锚点

1.1 高斯滤波 - Gaussian filtering

ED 的第一步与大多数图像处理方法相似：将图像与高斯核进行卷积以抑制噪声并平滑图像。 对于文中给出的所有结果，使用了 $\sigma = 1$ 的 $5\times5$ 的高斯核。

1.2 梯度幅值和边缘方向图的计算 - Computation of the gradient magnitude and edge direction maps

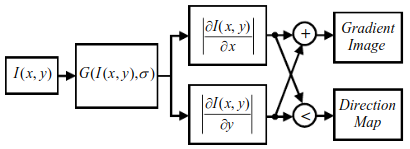
ED 的第二步是计算梯度大小和边缘方向图。使用平滑后图像，分别计算水平和垂直梯度 $G_x$ 和 $G_y$ 。任何著名的梯度算子，例如 Prewitt 、Sobel 和 Feldman 、Scharr 等，都可以用于此步骤。然后通过公式 $G = \sqrt{G_x^2 + G_y^2}$ 获得像素处的梯度幅度 $G$ 。另外，梯度大小可以通过简单地将 $G_x$ 和 $G_y$ 相加来计算，即 $G = |G_x| + |G_y|$，以加快计算速度，并且可以重新调整阈值。在计算梯度图的同时，还可以通过比较每个像素的水平和垂直梯度来计算边缘方向图。如果水平梯度较大，即 $|G_x| \geq |G_y|$，则假定有一条垂直边缘通过该像素。否则，就假定一条水平边缘通过该像素。实验表明，使用两个梯度方向就足以有效地用 Fig. 4-(b/c) 所示的路径机制对锚点的连接过程进行路径化。增加梯度角的数量只会增加计算时间，而不会改善锚点连接过程。

为了帮助抑制具有平滑强度变化的图像位置，对梯度图设置阈值并消除所谓的 “弱” 像素。 Fig. 3-(a) 显示了 Lena 图像以及相应的阈值梯度图。这个经过阈值处理的梯度集群代表了边缘区域，因为图像的所有边缘必须位于这个集群的边界内。换句话说，最终的边缘图将是这个集群的一个子集，被消除的黑色像素中没有一个包含边缘。ED 的前两个步骤（高斯滤波和梯度图计算）与大多数边缘检测算法相似。 然而，在边缘区域计算之后，ED 采用了一种非常非正统的方法：ED 不是测试边缘区域内的单个像素是否为边缘，而是首先发现像素的子集（称为锚点），然后通过一个智能启发式路径化程序连接这些锚点。

Fig. 3: Lena 的 (a) 阈值梯度集群，(b) 计算的锚点，(c) Lena 的最终边缘图由 ED 使用 (b) 中的锚点生成。

1.3 锚点的提取 - Extraction of the anchors

直观地讲，锚点应该对应于边缘将被覆盖的点。满足这一条件的点可以通过各种方式计算出来。例如，角落将是非常好的锚点候选者，因为它们位于图像上，其强度在水平和垂直方向上都有急剧变化。这种情况大大增加了边缘位于该位置的概率。一个旨在检测刚性几何物体的应用可能是一个很好的例子，可以选择角落作为锚点。另外，锚点提取程序可以根据应用专门设计，即为了性能，可以用一个兴趣点检测器或/和一个关键点描述符来代替检测图像上的特定边缘。因此，不必要的细节的边缘可以被过滤掉，不管它们有多尖锐。在本文中，作者倾向于使用局部梯度极值作为锚点，原因如下，即已经在前面的步骤中获得了计算局部梯度极值所需的信息，因此它简化了对算法主要思想的解释，并在计算上变得有利。请注意，锚点只是绘制边缘程序开始的一个位置，并不意味着每个锚点都会被包含在最终的边缘地图中。

如果把梯度图看成是三维的，那么锚点就会位于梯度图山的山峰上。为了连接连续的锚点，只需在梯度山的山峰上进行。 Fig. 2-(a/c) 显示了 Lena 帽子的部分梯度图，以及相应的三维视图。很明显，梯度算子在边缘交叉处产生最大值。也就是说，边缘位于梯度山的顶部。锚点（用红色圆圈标记）是这座山的山峰。 ED 将首先识别这些峰值，然后用智能路径程序连接它们。在 Fig. 2-(c) 中，两个箭头表示锚点的前进方向。

算法 1 显示了我们测试一个像素 $(x, y)$ 是否为锚点的直观算法。由于锚点必须是梯度图的局部峰值，我们只需将该像素的梯度值与它的邻居进行比较。对于水平边缘，我们比较上下邻居；对于垂直边缘，我们比较左右邻居。如果该像素的梯度值比它的两个邻居都大一定的阈值，那么该像素就被标记为一个锚点。通过改变锚点阈值，可以调整锚点的数量。锚点阈值越低，锚点就越密集。锚点阈值越高，锚点就越清晰，越稀疏。此外，锚点测试可以在不同的扫描间隔内进行，即每行/列，每隔二行/列等。增加锚的数量会增加边缘图的细节，反之亦然。根据不同的应用，不同的扫描间隔也可以用于水平和垂直锚点的计算，因此可以排除不需要的特征。锚点扫描间隔是可以独立调整的，然而，有一个重要的问题需要考虑。尽管边缘绘制算法具有固有的稳健性，但整体的边缘精度在一定程度上取决于锚点的选择和稀疏程度。尽管锚点搜索的扫描间隔是一个自由参数，但它必须保持在平滑核的半径以下（在这里提出的实验中恰好是 “5”），以确保没有突出的边缘特征被丢弃。这样一来，子采样（由于扫描间隔的选择）操作被保证保持在奈奎斯特速率以下，并避免获得模糊的结果。也可以采用多尺度的方法，通过尺度空间的方法改善边缘细节参数化。然而，目前的工作是引入新的边缘绘制范式，所以多尺度的概念被保留在本工作的范围之外，作为一个单独的案例研究。Fig. 3-(b) 显示了 Lena 图像的一组锚点，其锚点阈值为 8，扫描间隔为 4；也就是说，每隔 4 行或 4 列就扫描一次来寻找锚点。

1.4 通过智能路径连接锚点 - Connecting the anchors by smart routing

ED 最后也是最关键的一步是通过在锚点之间绘制边来连接锚点。 由于边缘图是在该步骤中使用算法前三个步骤中收集的信息构建的，因此该步骤值得特别注意。为了连接连续的锚点，只需从一个锚点到下一个锚点，在梯度图山的线状峰上前进。 该过程由算法第 2 步中计算的梯度幅度和边缘方向图指导。智能路径化过程独立于锚点提取方法， 从一个锚点开始，我们看一下通过锚点的边缘的方向。如果一条水平边穿过锚点，我们就开始向左和向右的连接过程（参考 Fig. 4-(b) ）。如果一条垂直的边穿过锚点，我们通过向上和向下进行连接过程（参考 Fig. 4-(c) ）。在移动过程中，只考虑三个直接邻居，并选择具有最大梯度值的那个。该过程在两种情况下停止：

1. 移出边缘区域，即当前像素的阈值梯度值为 0
2. 遇到了先前检测到的边缘。

算法 2 描述了从锚点 $(x,y)$ 开始的智能路径化。 假设一条水平边穿过这个锚点，给出的算法是在锚点左侧进行的。 向右、向上或向下进行非常相似，因此不再详细说明。 从锚点 $(x,y)$ 开始，只要满足上面列出的两个条件，就会向左移动。 在循环的每次迭代中，只需查看左侧的三个直接邻居，即 $(x-1,y-1)$、$(x-1,y)$ 和 $(x-1,y+1)$，以及 选择具有最大梯度值的那个。 如果向右走，会考虑右边的三个直接邻居，即 $(x+1,y-1)$、$(x+1,y)$ 和 $(x+1,y+1)$。

Fig. 4-(a) 给出了智能路径化程序的详细说明，它是在一个经过阈值处理的梯度集群的放大区域上。像素内的数字是梯度的大小；黑色的像素代表阈值化的像素。锚点用红色的圆圈标记，连接过程中收集的像素用黄色圆圈标记。假设 $(8,4)$ 处的像素是起始锚点。因为有一条水平线穿过这个锚点，所以开始了水平行走（先向左走，然后向右走）。小箭头表示路径化过程中所考虑的像素，蓝色箭头表示所选的像素。如 Fig. 4-(b/c) 所示，在每次迭代时都会检查三个紧邻的边缘方向，并选择具有最大梯度值的像素。在 (3,5) 处，边缘的方向从水平方向变为垂直方向。在这一点上，停止当前的水平左行，并开始两个垂直行，一个向上走，一个向下走。垂直向上行走立即终止，因为它将选择已经选定的边段像素 (4,4)。垂直向下行走一直持续到 (5,10)。请注意，同一边缘段内可能有许多不同的行走。也就是说，在提取一个边缘段的过程中，我们可能会在水平和垂直方向上多次移动，如 Fig. 4 所示，有一次水平左移，一次垂直下移。同时注意到，所得到的边缘段总是连续的，而且是一像素宽。所有锚点不一定都要包括在最终的边缘图中。如果一些边缘段由少于特定数量的锚点或边缘组成，就可以舍弃这些边缘段。这种简单的控制可以通过毫不费力地排除短而小的结构来改进最终的边缘图。

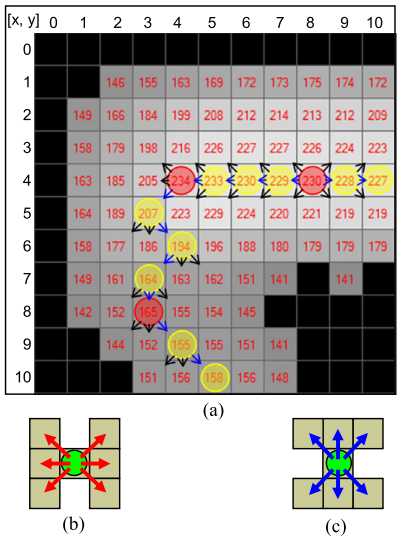
Fig. 4: (a) 智能路径化程序的图示，(b) 水平进行，(c) 垂直进行。

作者的算法实现 CihanTopal/ED_Lib ，效果如下图

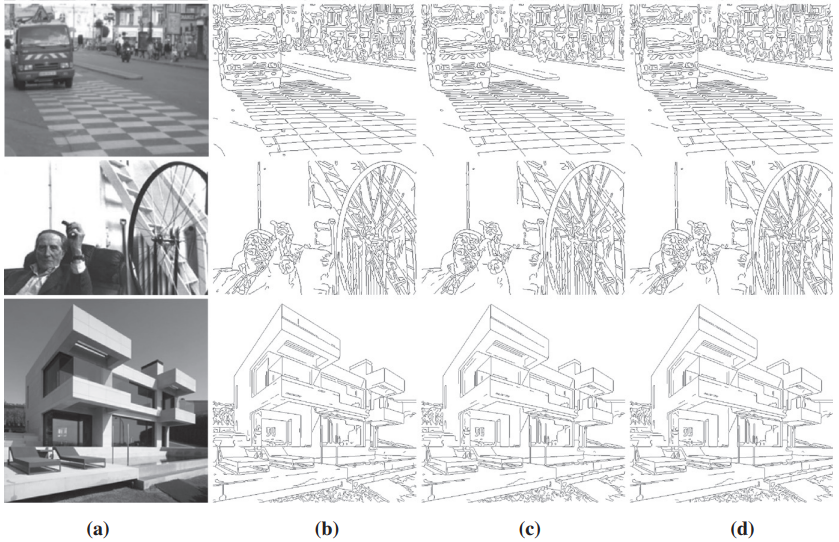
(a) 原始图像。 (b–d) ED 的边缘图分别使用 Prewitt、Sobel 和 Scharr 梯度算子。梯度阈值、锚点阈值对分别为：Prewitt (24, 5)、Sobel (36, 8) 和 Scharr (144,32)。

Reference