DynaVINS: 适用于动态环境的 VI-SLAM

DynaVINS: A Visual-Inertial SLAM for Dynamic Environments ¹

SLAM 算法在各种机器人应用中被广泛利用，这些应用需要在 GPS 信号受阻的环境中进行精确定位或导航。各种类型的传感器已被用于 SLAM 算法中。特别是视觉传感器，由于其成本和重量相对较低，信息丰富而被广泛使用。各种视觉 SLAM 方法已经被研究了许多年，然而，大多数研究人员都假设地标是隐性的静态的。因此，许多视觉 SLAM 方法在与包含各种动态物体的现实世界环境互动时仍有潜在风险。

近些年来开始有研究专注于仅仅使用视觉传感器来处理动态物体。多数研究通过深度聚类、特征重投影或深度学习来检测动态物体的区域来解决这些问题。此外，也有一些研究将物体的动态性纳入优化框架。然而，基于几何学的方法需要准确的相机姿势，因此只能处理有限的动态物体部分；而基于深度学习辅助的方法有一个局限性，即只适用于预定的物体。

同时，视觉-惯性 SLAM（VI-SLAM）框架也逐渐被广泛使用。将惯性测量单元（IMU）集成到视觉 SLAM 中，与纯视觉 SLAM 不同，来自 IMU 的运动先验有助于 VI-SLAM 算法在一定程度上容忍有动态物体的场景。然而，如 Fig.1-(b) 所示，如果主要的动态物体遮挡了大部分的视野，那么仅仅使用运动先验就无法解决问题。此外，在现实世界的应用中，暂时静止的物体在被观察时是静止的，但在不被观察时是运动的。如 Fig.1-(c) 所示，这些物体可能会因为误检而导致回环过程的严重失败。

Fig. 1 : DynaVINS 在各种动态环境中的表现。(a)–(b) VIODE 数据集的 city_day 序列中的特征剔除结果。即使大多数特征是动态的，DynaVINS 也能摒弃动态特征的影响。(c) 在作者实验的数据集的E形状序列中，将特征匹配结果分离成多个假设。即使存在一个暂时的静态物体，也只有来自静态物体的假设被确定为误检测。在这两种情况下，高权重和低权重的特征分别表示为绿色圆圈和红色十字。

在这项研究中，为了解决上述问题，提出了一个稳健的 VI-SLAM 框架，称为 DynaVINS，它对动态和临时静态对象具有稳健性。具体贡献总结如下：

• 提出了稳健的 VI-SLAM 方法来处理占主导地位的、未定义的动态物体，这些物体不能仅仅通过基于学习的方法或纯视觉方法来解决
• 提出了一个新的光束平差法（BA）处理流程管道（见 Fig.2），用于同时估计摄像机的位置和放弃动态物体中明显偏离运动先验的特征
• 提出了一个强大的全局优化，其约束条件被分组为多个假设，以拒绝来自暂时静态物体的持续循环闭合

Fig. 2 : 在传感器预处理步骤中，对单目或双目图像的特征进行跟踪，并对 IMU 数据进行预积分。然后，应用鲁棒的 BA 来丢弃动态物体的跟踪特征，只保留静态物体的特征。利用跟踪特征的数量对关键帧进行分组，并在当前关键帧组中检测到的回环被聚类到假设中。在选择性优化中使用或拒绝每个具有权重的假设。使用所提出的框架，可以得到一个对动态和临时静态物体具有鲁棒性的轨迹。

1. 鲁棒的光束平差 - Robust Bundle Adjustment

1.1 符号 - Notation

在文章中规定以下符号。第 $i$ 帧相机和第 $j$ 个跟踪的特征分别表示为 $C_i$ 和 $f_j$ 。对于两帧 $C_A$ 和 $C_B$ ，$T_B^A \in SE(3)$ 表示 $C_A$ 相对于 $C_B$ 的姿态。而 $C_A$ 在世界坐标系 $W$ 中的姿态表示为 $T_W^A$ 。$\mathcal B$ 是一组 IMU 预积分的序列，而 $\mathcal P$ 是一组视觉对 $(i,j)$ ，其中 $i$ 对应于帧 $C_i$ ， $j$ 对应于特征 $f_j$ 。由于特征 $f_j$ 是在多个相机帧中追踪的，不同的相机帧可以包含相同的特征 $f_j$ 。因此，当前移动窗口中所有被跟踪的特征的索引集合表示为 ${\bf F}_{\mathcal P}$ ，包含特征 $f_j$ 的相机帧的索引合集表示为 ${\mathcal P}(f_j)$ 。在当前滑动窗口的视觉-惯性优化框架中，$\mathcal X$ 代表完整的状态向量，其中包含关键帧的姿势和速度、IMU 的偏置，即加速度和陀螺仪偏置，以及估计的特征深度的集合。

1.2 常规的光速平差法 - Conventional Bundle Adjustment

在常规的视觉-惯性状态估计器中，视觉-惯性 BA 的定义如下：

$$ \min _{\mathcal X} \left\lbrace \big\lVert {\bf r}_p - {\bf H} _p {\mathcal X} \big\rVert^2 + \sum _{k \in {\mathcal B}} \big\lVert {\bf r} _{\mathcal I} (\hat {\bf z}^{b_k} _{b _{k+1}}, {\mathcal X}) \big\rVert _{{\bf P}^{b_k} _{b _{k+1}}} ^2 + \sum _{(i,j) \in {\mathcal P}} \rho_H \big( \big\lVert {\bf r} _{\mathcal P} (\hat {\bf z}_j^{C_i}, {\mathcal X}) \big\rVert _{{\bf P} _j^{C_i}}^2 \big) \right\rbrace \tag{1.1} \label{1.1} $$

其中，$\rho_H(\cdot)$ 表示 Huber 损失函数，${\bf r}_p \ , {\bf r} _{\mathcal I}$ 和 ${\bf r} _{\mathcal P}$ 分别表示边缘化、IMU 和视觉重投影测量的残差，$\hat {\bf z}^{b_k} _{b _{k+1}}$ 和 $\hat {\bf z}_j^{C_i}$ 分别代表 IMU 和特征点的观测，${\bf H}_p$ 表示边缘化的测量估计矩阵，$\bf P$ 表示每个项的协方差。为了方便起见，${\bf r} _{\mathcal I} (\hat {\bf z}^{b_k} _{b _{k+1}}, {\mathcal X})$ 和 ${\bf r} _{\mathcal P} (\hat {\bf z}_j^{C_i}, {\mathcal X})$ 分别简化为 ${\bf r} _{\mathcal I}^k$ 和 ${\bf r} _{\mathcal P}^{j, i}$ 。

一旦 outliers 的比例增加，Huber 损失函数就不能成功工作。这是因为 Huber 损失函数并不能完全拒绝 outliers 的残差。另一方面，重新降序的 M 估计法 (M-estimators)，如 Geman-McClure（GMC），由于它们的 zero-gradients，一旦残差超过一个特定的范围，就完全忽略了 outliers 。不幸的是，这种截断引发了一个问题，即被认为是 outliers 的特征将永远不会再成为 inliers，即使这些特征来源于静态物体。

为了解决这些问题，作者提出的 BA 方法由两部分组成：

1. 利用 IMU 预积分的正则化因子
2. 考虑每个权重的先前状态的动量因子，以涵盖预积分变得暂时不准确的情况

1.3 正则化因子 - Regularization Factor

首先，为了拒绝离群的特征，同时稳健地估计姿势，提出了一个新的损失项，其灵感来自 Black-Rangarajan 对偶性 (B-R duality) ²，具体如下： $$ \rho (w_j, {\bf r}^j_{{\mathcal P}}) = w_j^2 {\bf r}^j_{{\mathcal P}} + \lambda_w \Phi^2(w_j) \tag{1.2} \label{1.2} $$

其中，为了简单起见 ${\bf r}^j_{{\mathcal P}}$ 表示 $\sum_{i\in{\mathcal P}(f_j)} \lVert {\bf r} _{\mathcal P}^{j, i} \rVert^2$ ，$w_j \in [0, 1]$ 表示每个特征 $f_j$ 对应的权重，$w_j$ 接近 $1$ 的特征 $f_j$ 被确定为静态特征，$\lambda_w \in {\mathbb R}^+$ 是一个常量参数，$\Phi(w_j)$ 表示权重 $w_j$ 的正则化因子，定义如下：

$$ \Phi(w_j) = 1 - w_j \tag{1.3} \label{1.3} $$

然后，采用式 $\eqref{1.2}$ 中的 $\rho (w_j, {\bf r}^j_{{\mathcal P}})$ 替代式 $\eqref{1.1}$ 中视觉重投影项中的 Huber 范数。因此，BA 公式可以表示为：

$$ \min _{\mathcal{X, W}} \left\lbrace \big\lVert {\bf r}_p - {\bf H} _p {\mathcal X} \big\rVert^2 + \sum _{k \in {\mathcal B}} \big\lVert {\bf r} _{\mathcal I}^k \big\rVert^2 + \sum _{j \in {\bf F} _{\mathcal P}} \rho (w_j, {\bf r}^j _{{\mathcal P}}) \right\rbrace \tag{1.4} \label{1.4} $$

其中，$\mathcal W = \lbrace w_j | j \in {\bf F}_{\mathcal P} \rbrace$ 代表所有权重的集合。通过采用受 B-R 对偶启发的权重和正则化因子，在保持状态估计性能的同时，可以减少与估计状态相比具有高重射误差的特征的影响。细节将在下文进行展开。

式 $\eqref{1.4}$ 可以使用交替优化求解²。因为当前状态 $\mathcal X$ 可以从 IMU 预积分和先前的优化状态中估计出来，$\mathcal W$ 首先用固定的 $\mathcal X$ 更新。然后，用固定的 $\mathcal W$ 优化 $\mathcal X$ 。在优化 $\mathcal W$ 时，除权重外的所有项都是常量。因此，优化权重的公式可以表达如下：

$$ \min_{\mathcal W} \left\lbrace \sum_{j \in {\bf F} _{\mathcal P}} \rho (w_j, {\bf r} _{\mathcal P}^j) \right\rbrace \tag{1.5} \label{1.5} $$

因为权重 $w_j$ 是相互独立的，所以式 $\eqref{1.5}$ 可以对每个 $w_j$ 进行独立优化，如下所示：

$$ \min_{w_j \in [0, 1]} \left\lbrace w_j^2 \Big( \sum_{i \in \mathcal P (f_i)} \big\lVert {\bf r}_{\mathcal P}^{j, i} \big\rVert^2 \Big) + \lambda_w \Phi^2 (w_j) \right\rbrace \tag{1.6} \label{1.6} $$

由于式 $\eqref{1.6}$ 是关于 $w_j$ 的二次形式，因此可以得出最佳 $w_j$ 如下（对 $w_j$ 求一阶导，并令导数等于 $0$ ，易得）：

$$ w_j = \frac{\lambda_w}{{\bf r}_{\mathcal P}^j + \lambda_w} \tag{1.7} \label{1.7} $$

如前所述，权重首先根据估计状态进行优化。因此，具有重投影误差的特征的权重从小值开始。然而，如 Fig.3-(a) 所示，除非权重为零，否则特征 $\rho(w_j, {\bf r} _{\mathcal P}^j)$ 的损失是一个凸函数，不仅在 outliers 的特征的损失中存在非零梯度，而且在 inliers 的特征的损失中也存在非零梯度，所以，无论使用何种类型的损失函数，这意味着新的特征在一开始就会影响 BA 。在重复优化步骤直到状态和权重收敛的同时，outlier 特征的权重被降低，其损失也更加扁平化。因此，outlier 特征的损失接近零梯度并且不再会影响 BA 。收敛后，可以用式 $\eqref{1.7}$ 来表示重投影误差的权重。因此，收敛后的损失 $\bar \rho ({\bf r} _{\mathcal P}^j)$ 可以通过将式 $\eqref{1.7}$ 应用于式 $\eqref{1.2}$ 得出，具体如下：

$$ \bar \rho ({\bf r} _{\mathcal P}^j) = \frac{\lambda_w {\bf r} _{\mathcal P}^j}{\lambda_w + {\bf r} _{\mathcal P}^j} \tag{1.8} \label{1.8} $$

如 Fig.3-(b) 所示，增加 $\lambda_w$ 会在两个方向上影响 $\bar \rho ({\bf r} _{\mathcal P}^j)$ : 增加梯度值和凸性。通过增加梯度值，视觉重投影残差对 BA 的影响要大于边缘化和 IMU 预积分残差。而通过增加凸度，一些 outlier 的特征会影响 BA 。总而言之，所提出的因子通过以自适应的方式调整权重，同时受益于Huber loss 和 GMC ，上述方法能够有效地过滤掉了 outliers ，美中不足的是优化一开始时并不能完全忽略掉的 outliers 。

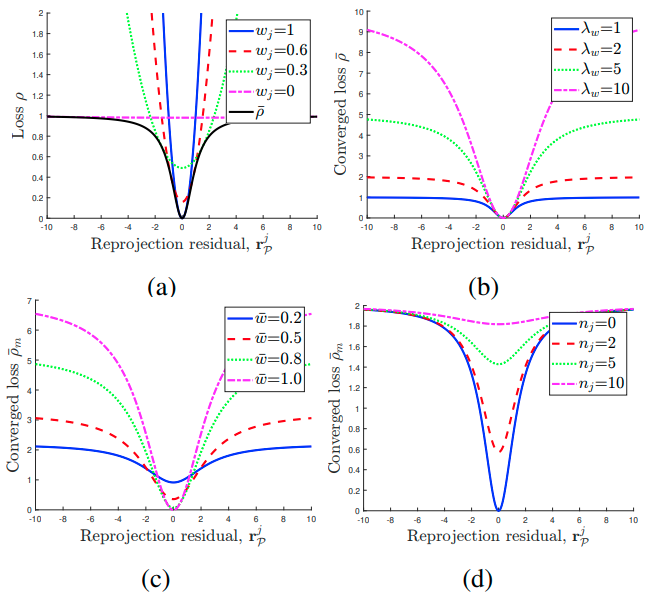
Fig. 3 : (a) 当 $\lambda_w = 1$ 时，$\rho(w_j, {\bf r}^j _{\mathcal P})$ 关于 $w_j$ 交替优化中的变化， $\bar \rho ({\bf r} _{\mathcal P}^j)$ 表示收敛的损失函数。(b) $\bar \rho ({\bf r} _{\mathcal P}^j)$ 相对于 $\lambda_w$ 的变化。(c) 当 $n_j = 5$ 时，$\bar \rho_m ({\rm r}^j _{\mathcal P})$ 关于 $\bar w_j$ 的变化。(d) 当 $\bar w_j = 0$ 时， $\bar \rho_m ({\bf r} _{\mathcal P}^j)$ 关于 $n_j$ 的变化。

1.4 权重动量因子 - Weight Momentum Factor

当运动变得激进时，IMU的预积分变得不精确，因此估计的状态变得不准确。在这种情况下，来自静态物体的特征的重投影残差变得更大，因此，通过正则化因子，这些特征将在 BA 过程中被忽略，即使以前的权重接近于 1 。如果增加 $\lambda_w$ 来解决这个问题，即使是动态对象的高重射残差的特征也会被使用。因此，BA 的结果将是不准确的。因此，增加 $\lambda_w$ 并不足以解决这个问题。为了解决这个问题，提出了一个额外的因子，即权重动量因子，以使先前估计的特征权重不受激进运动的影响。由于特征是连续跟踪的，所以每个特征 $f_j$ 用它以前的权重 $\bar w_j$ 进行了 $n_j$ 次优化。为了使当前的权重倾向于保持在 $\bar w_j$ 并且随着 $n_j$​ 的增加而增加倾向的程度，权重动量因子 $\Psi(w_j)$ 被设计如下： $$ \Psi (w_j) = n_j (\bar w_j - w_j) \tag{1.9} \label{1.9} $$ 然后，将式 $\eqref{1.9}$ 加入到 $\eqref{1.2}$ 中，可以得出修改后的损失项，如下所示： $$ \rho_m (w_j, {\bf r} _\mathcal P^j) = w_j^2 \sum _{i \in \mathcal P (f_i)} \big\lVert {\bf r} _\mathcal P^{j, i} \big\rVert^2 + \lambda_w \Phi^2(w_j) + \lambda_m \Psi^2(w_j) \tag{1.10} \label{1.10} $$

其中 $\lambda_m \in {\mathbb R}^+$ 表示一个常数参数，用于调整动量因子对 BA 的影响。综上所述，所提议的鲁棒 BA 可以用 Fig.4 来说明。追踪到的特征的先前权重被用于权重动量因子，而当前窗口中所有特征的权重被用于正则化因子。因此，鲁棒 BA 表示如下：

$$ \min _{\mathcal{X, W}} \left\lbrace \big\lVert {\bf r}_p - {\bf H} _p {\mathcal X} \big\rVert^2 + \sum _{k \in {\mathcal B}} \big\lVert {\bf r} _{\mathcal I}^k \big\rVert^2 + \sum _{j \in {\bf F} _{\mathcal P}} \rho_m (w_j, {\bf r}^j _{{\mathcal P}}) \right\rbrace \tag{1.11} \label{1.11} $$

式 $\eqref{1.11}$ 可以通过使用与 $\eqref{1.4}$ 相同的方法进行交替优化来解决。交替优化迭代到 $\mathcal X$ 和 $\mathcal W$ 收敛为止。那么，可以得到收敛的损失项 $\bar \rho_m ({\bf r} _{\mathcal P}^j)$ 。 $\bar \rho_m ({\bf r} _{\mathcal P}^j)$ 与 $\bar w_j$ 和 $n_j$ 的关系分别如 Fig.3-(c) 和 Fig.3-(d) 所示。如 Fig.3-(c) 所示，如果 $\bar w$ 很低，即使 ${\bf r} _\mathcal P^j$ 接近于 0，损失的梯度也很小。因此，推测来源于动态物体的特征对 BA 的影响不大，即使它们在当前步骤中的重投影误差很低。此外，如 Fig.3-(d) 所示，如果 $\bar w_j$ 为零，梯度会随着 $n_j$ 的增加而变小，因此，跟踪的 outlier 特征对 BA 的影响较小，而且跟踪的时间越长，对 BA 的影响越小。对于双目相机的配置，除了在一个相机上的重投影外，在同一关键帧的另一个相机上的重投影 ${\bf r} _\mathcal P^{stereo}$ ，或另一个关键帧的 ${\bf r} _\mathcal P^{another}$ 也存在。在这种情况下，权重也适用于重投影 ${\bf r} _\mathcal P^{another}$ ，因为它也受到特征移动的影响，而 ${\bf r} _\mathcal P^{stereo}$ 对特征的移动是不变的，只被作为深度估计的标准。

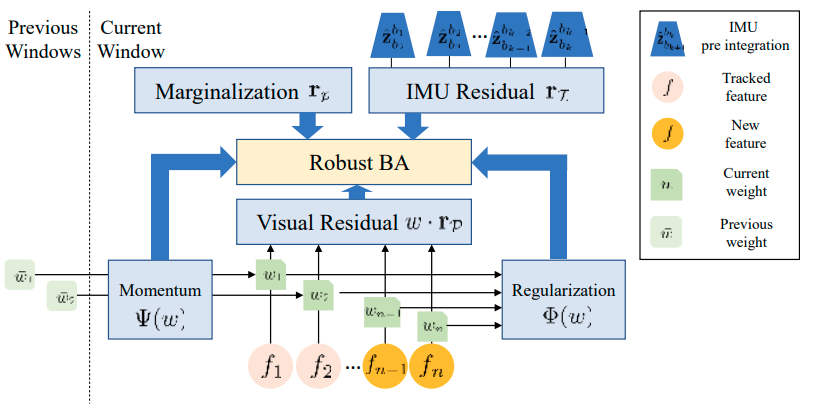
Fig. 4 : 鲁棒 BA 结构框架。每个特征都有一个权重，并被用于视觉残差。每个权重都通过正则化因子和权重动量因子进行了优化。预积分 IMU 数据被用于 IMU 残差项。所有的参数都在鲁棒 BA 中进行了优化。

2. 选择性全局优化 - Selective Global Optimization

在 VIO 框架中，沿着轨迹累积漂移是不可避免，因为优化只在移动窗口内进行。因此，例如使用 DBoW2 的回环检测，对于优化所有轨迹是必要的。在一个典型的视觉 SLAM 中，所有的回环链路都被利用，即使其中一些是来自暂时静止的物体。这些错误回环可能导致 SLAM 系统的崩溃。此外，来自临时静态物体和静态物体的特征可能存在于同一个关键帧中。因此，在下文中，提出了一种方法来消除错误回环链路，同时保持真正回环链路。

2.1 关键帧分组 - Keyframe Grouping

与传统的单独处理回环的方法不同，将来自相同特征的回环被分组，即使它们来自不同的关键帧。因此，每组只使用一个权重，可以更快地进行优化。如 Fig.5-(a) 所示，在分组之前，相邻的关键帧必须至少共享最低数量的跟踪特征，才能进行分组。从第 $i$ 个摄像机帧 $C_i$ 开始的分组定义如下： $$ Group(C_i) = \lbrace C_k | \ |{\bf F}_i^k| \geq \alpha, k \geq i \rbrace \tag{2.1} \label{2.1} $$ 其中，$\alpha$ 表示跟踪特征的最小数量，${\bf F}_i^k$ 表示从 $C_i$ 到 $C_k$ 跟踪的特征集合。为简单起见，下文中 $Group(C_i)$ 将被记为 $G_i$ 。

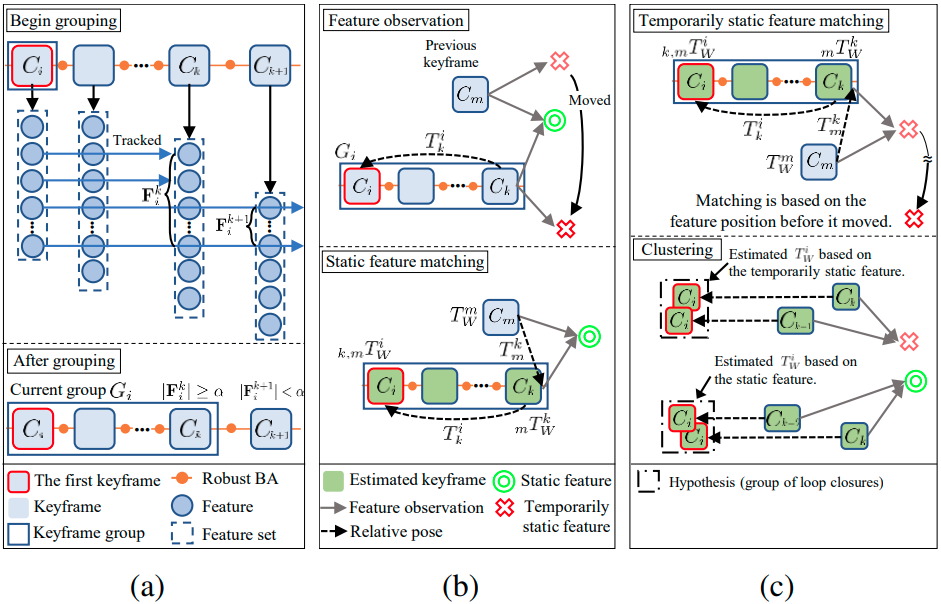
Fig. 5 : 多重假设聚群的过程。(a) 共享最小数量的跟踪特征的关键帧被分组。(b) 有两种类型的特征用于匹配：静态特征和临时静态特征。$C_i$ 的估计姿态 $_{k,m}T_W^i$ 可以使用匹配结果 $T_m^k$ 和局部相对姿态 $T_k^i$ 来估计。如果使用静态特征进行匹配，则可以估计出准确的关键帧姿态。(c) 临时静态特征从之前的位置移动。 由于匹配结果是基于特征的先前位置。 因此，估计的关键帧姿态将是不准确的。 最后，基于欧几里德距离对具有相似 $T^i_W$ 的特征匹配结果进行聚类。

2.2 多重假设聚群 - Multiple Hypotheses Clustering

在上一小节中对关键帧进行分组后，使用 DBoW2 从 $C_i (C_k \in G_i \ {\rm and} \ m < i)$ 开始识别当前组 $G_i$ 中与每个关键帧 $C_k$ 相似的关键帧 $C_m$ 。注意，如果没有相似的关键帧，则跳过 $C_k$ 。在为 $k$ 识别出最多三个不同的 $m$ 之后，在 $C_k$ 和这些关键帧之间进行特征匹配，可以得到相对位姿 $T^k_m$ 。依据 $T^k_m$ ，$C_k$ 在世界坐标系中的估计位姿 $_mT_W^k$ ，如下所示： $$ _mT_W^k = T_m^k \cdot T_W^m \tag{2.2} \label{2.2} $$ 其中，$T_W^m$ 表示为 $C_m$ 在世界坐标系下的姿态。然而，很难直接计算当前组中不同关键帧与回环帧的相似性。假设 $C_k$ 和 $C_i$ 之间的相对姿态 $T_k^i$ 足够准确， $C_i$ 在世界帧中的估计姿态可以表示如下： $$ _{k,m}T_W^i = T_k^i \cdot _mT_W^k \tag{2.3} \label{2.3} $$ 如果用于匹配的特征来自同一个物体，那么即使匹配的 $C_k$ 和 $C_m$ 不同，匹配的估计 $T_W^i$ 也会位于彼此附近。因此，在计算了闭合环路的估计 $T_W^i$ 之间的欧氏距离后，可以将欧氏距离小的类似闭合环路进行聚类，如 Fig.5-(c) 所示。根据选择哪一个环路闭合集群，来自图形优化的轨迹结果是不同的。因此，每个集群可以被称为一个假设。为了减少计算成本，通过比较假设内回环集群的个数 (cardinality) ，采用最排前的两个假设。当前组 $G_i$ 的这两个假设被表示为 $H_i^0$ 和 $H_i^1$ 。然而，目前还无法区分真假检测假设。因此，在候选假设中确定正确检测假设的方法将在下一节描述。

2.3 约束群的选择性优化 - Selective Optimization for Constraint Groups

今年来的视觉 SLAM 算法大多数使用图优化。让 $\mathcal C, \mathcal T, \mathcal L$ 和 $\boldsymbol W$ 分别表示关键帧、姿态、回环和所有权重的集合。那么，图优化可以表示为：

$$ \min_\mathcal T \Big\lbrace \underbrace{ \sum _{i \in \mathcal C} \big\lVert {\bf r}(T _{i+1}^i, \mathcal T) \big\rVert^2 _{{\bf P} _{T^i} ^{T^{i+1}}} } _{\rm local \ \ edge} + \underbrace{ \sum _{(j,k) \in \mathcal L} \rho_H \big\lVert {\bf r} (T_k^j , \mathcal T) \big\rVert^2 _{{\bf P} _{\mathcal L} } } _{\rm loop \ \ closure \ \ edge} \Big\rbrace \tag{2.4} \label{2.4} $$

其中，$T_{i+1}^i$ 表示两个相邻关键帧 $C_i$ 和 $C_{i+1}$ 之间的局部姿态，$T_k^j$ 是来自回环 $C_j$ 和 $C_k$ 之间的相对姿态，${\bf P} _{T^i}^{T^{i+1}}$ 和 ${\bf P} _{\mathcal L}$ 分别表示局部姿态和回环的协方差。对于 $G_i$ 组的两个假设，权重表示为 $w_i^0$ 和 $w_i^1$ ，权重之和表示为 $\boldsymbol w_i$ ，假设集表示为 $\mathcal H$ 。使用与 1.3 节 类似的程序，Black-Rangarajan 对偶性被应用于式 $\eqref{2.4}$ ，如下所示：

$$ \begin{align*} & \min_{\mathcal{T}, {\boldsymbol W}} \bigg\lbrace \sum _{i \in \mathcal C} \big\lVert {\bf r}(T _{i+1}^i, \mathcal T) \big\rVert^2 _{{\bf P} _{T^i}^{T^{i+1}}} \ \ + \newline & \sum _{H_i \in \mathcal H} \Big( \underbrace{ \big( \sum _{(j,k) \in H_i^0} \big\lVert \frac{w_i^0}{|H_i^0|} {\bf r}(T_k^i, \mathcal T) \big\rVert^2 _{{\bf P} _\mathcal L} \big) } _{\rm residual \ for \ hypothesis \ 0} + \underbrace{ \big( \sum _{(j,k) \in H_i^1} \big\lVert \frac{w_i^1}{|H_i^1|} {\bf r}(T_k^i, \mathcal T) \big\rVert^2 _{{\bf P} _\mathcal L} \big) } _{\rm residual \ for \ hypothesis \ 1 \ (optional) } + \underbrace{ \lambda_l \Phi_l^2(\boldsymbol w_i) } _{\rm hypothesis \ regularization \ function} \Big) \bigg\rbrace \end{align*} \tag{2.5} \label{2.5} $$

其中，$\lambda_l \in {\mathbb R}^+$ 是一个常量常数。回环的正则化系数 $\Phi_l$ ，定义如下： $$ \Phi_l (\boldsymbol w_i) = 1 - \boldsymbol w_i = 1 - (w_i^0 + w_i^1) \tag{2.6} \label{2.6} $$ 其中，$w_i^0,w_i^1 \in [0, 1]$ 。为了确保权重不受假设中闭环次数的影响，权重除以每个假设中回环集群个数 (cardinality) 。然后，式 $\eqref{2.5}$ 以与式 $\eqref{1.11}$ 相同的方式进行优化。相应地，在优化过程中只采用权重高的假设。当所有假设由于多个临时静态对象而为误报时，所有权重都可以接近于 0。因此，可以防止由误报假设引起的失败。由于关键帧的姿势在优化后发生了变化，所以在下一次优化时，要对所有组别再次进行 2.2 节 的假设聚类。

Reference