A micro Lie theory for state estimation in robotics ¹

在过去的几年里，机器人界为正确制定估计问题做出了巨大的努力。这是因为对解决方案的精度、一致性和稳定性的要求越来越高。事实上，对状态和测量、相关函数及其不确定性的正确建模对于实现这些目标至关重要。这导致了涉及所谓 “流形” 的设计，在这种情况下，流形不亚于状态表征演化的李群的光滑拓扑表面。依靠李氏理论 (Lie Theory, LT) ，我们能够构建一个严格的微积分理论来精确和轻松地处理不确定性、导数和积分。通常，这些工作都集中在众所周知的旋转 $SO(3)$ 和刚性运动 $SE(3)$ 流形上。

当第一次引入李群时，尝试从不同的角度看待它们是很重要的。拓扑学的观点，见 Fig. 1 ，涉及流形的形状，并传达其与切线空间和指数映射关系的直观感受。代数学观点涉及群运算及其具体实现，允许利用代数特性来开发闭合形式的公式或简化这些公式。几何学的观点，在机器人学中特别有用，利用群组元素将物体自身和参考坐标系的位置、速度、方向和 (/或) 其他修改联系起来。原点坐标系可以与群组的特性相联系，流形上的任何其他点都代表某个 “局部 “坐标系。通过诉诸这些类比，LT 的许多数学抽象可以更接近于矢量空间、几何学、运动学和其他更经典领域的直观概念。

Representation of the relation between the Lie group and the Lie algebra

Fig. 1: 李群和李代数之间关系的表示。李代数 $T_\varepsilon \cal{M}$ （红色平面）是李群流形 $\cal M$ （此处表示为蓝色球体）在特征 $\varepsilon$ 处的切线空间。通过指数映射，在李代数上通过原点的每条直线路径 ${\rm v}t$ 都会产生一条围绕流形的路径 $\exp({\rm v}t)$ ，该路径沿各自的测地线 (geodesic) 运行。反过来说，群的每个元素在李代数中都有一个等价物。这种关系是如此深刻，以至于（几乎）所有曲线和非线性群中的操作在李代数（线性向量空间）中都有一个精确的等价物。尽管 ${\mathbb R}^3$ 中的球体不是一个李群（我们只是把它作为一个可以画在纸上的表示），但 ${\mathbb R}^4$ 中的球体是，它描述的是单位四元数的群 – 见 Fig. 4 和 Ex. 5 。

李氏理论绝非简单。为了掌握 LT 的最低概念，可以考虑以下三个参考资料。首先，Abbaspour 的 “Basic Lie theory”²有 400 多页。Howe 的 “Very basic Lie theory”³也有类似的标题，有 24 页（密集的），有时被认为是必读的介绍。最后，更现代的、经常被人称道的 Stillwell 的 “Naive Lie theory”⁴有 200 多页。有了这些被称为 “basic”、“very basic " 和 “naive” 的先例，本文仅有 17 页，目的是将李氏理论进一步简化（因此作者在标题中使用了形容词 “微观”）。作者通过两种方式做到这一点。首先，从李氏理论中选择一个小的材料子集。这个子集是如此之小，以至于它仅仅探索了 LT 的潜力。然而，它对于我们在机器人技术中处理的那种估计问题（如惯性预积分、里程计和 SLAM、视觉伺服等）中的不确定性管理似乎非常有用，从而使优雅而严格的最佳优化器设计成为可能。第二，作者以教学的方式对其进行解释，以便进一步减少学习 LT 的门槛，这仍然是需要的。也就是说，作者坚持在这个方向上的努力，用一个典范的标题（Stillwell ⁴）来命名，并提供了一个更简化的版本。正文的主体是通用的，尽管作者试图将抽象程度降到最低。插入的例子作为应用于已知组（旋转和运动矩阵、四元数等）的一般概念的基础。此外，大量的数字加上非常详细的说明，再次解释了相同的概念。作者特别关注 jacobians 的计算，这对大多数最优估计器来说是必不可少的，也是设计新算法时很多麻烦的来源。作者提供了一个章节，其中包含一些机器人定位和建图的应用示例，实现了 EKF 和基于 LT 的非线性优化算法。最后，几个附录包含了机器人学中最常用的群组的相关细节的充分参考：单位复数、四元数、二维和三维旋转矩阵、二维和三维刚性运动矩阵，以及微不足道的平移群组。

作者对李氏理论最重要的简化是在范围方面。Howe³ 的以下一段话可以帮助作者说明作者精简后剩下的基础内容: “李氏理论的基本现象是，人们可以以一种自然的方式将李群 $\mathcal G$ 与它的李代数 $\mathfrak g$ 联系起来。李代数 $\mathfrak g$ 首先是一个矢量空间，其次是被赋予一个称为李氏括号 […] 的双线性非关联积。令人惊讶的是，群 $\mathcal G$ 几乎完全由 $\mathfrak g$ 及其李括号决定。由于 $\mathcal G$ 是一个复杂的非线性对象，而 $\mathfrak g$ 只是一个矢量空间，通常使用 $\mathfrak g$ 会简单得多。[…] 是李氏理论的力量来源之一。” 对此，Stillwell 在 ⁴ 中甚至谈到了 “the miracle of Lie theory”。在这项工作中，作者将有效地把李代数降到第二平面，而支持其等价的向量空间 ${\mathbb R}^n$ ，并且完全不引入李括号。因此，李群和它的李代数之间的联系在这里就不再深究了。作者写此论文的立场是，鉴于所预见的目标应用领域，这种材料往往是不必要的。因为，如果包括在内，那么将无法实现清晰和有用的目标，因为读者将不得不去了解那些因其抽象或微妙而不必要的复杂的数学概念。

作者的努力与最近关于这一主题的其他文献 ⁵, ⁶, ⁷ 相一致，这些文献也确定了使 LT 更接近机器人学家的需要。作者的方法旨在让本文的目标读者感到熟悉：一个熟练掌握状态估计（卡尔曼滤波、基于图的优化等），但尚未熟悉李氏理论的理论库的读者。为此，在符号方面采取了一些举措，特别是在导数的定义方面，使其接近于矢量的对应物，从而使链式法则清晰可见。如前所述，作者选择实际上避免使用属于李代数特有的材料，而倾向于在其同构切向空间 ${\mathbb R}^n$ 上工作，这是最终表示不确定性或（小）状态增量的地方。所有这些步骤都是在绝对不损失精度或精确性的情况下进行的，作者相信它们会使对 LT 的理解和对其工具的操作更加容易。

本文附有一个新的开源 C++ 头文件库，名为 manif ⁸，可以在 https://github.com/artivis/manif 找到。 manif 实现了广泛使用的 $SO(2)$、$SO(3)$、$SE(2)$ 和 $SE(3)$ 群，并支持创建解析性 jacobians。该库的设计旨在实现易用性、灵活性和性能。

1. 微观的李氏理论 - A MICRO LIE THEORY

1.1 李群 - The Lie group

李群在一个独特的主体中包含了群和光滑流形的概念：李群 $\mathcal G$ 是一个其元素满足群公理的光滑流形。在把这两个概念结合起来之前，先简要地介绍一下这两个概念。一方面，可微或光滑流形是一个局部类似于线性空间的拓扑空间。读者应该能够直观地了解流形的概念 (Fig. 2) ：它就像一个弯曲的、光滑的（超）表面，没有边缘或尖峰，嵌入在一个高维的空间中。在机器人学中，我们说我们的状态矢量在这个表面上演化，也就是说，流形描述或由施加在状态上的约束来定义。例如，具有单位规范约束的向量定义了一个半径为 1 的球面流形。流形的平滑性意味着在每个点上都存在一个唯一的切线空间。这个空间是一个线性空间或向量空间，我们可以在上面进行微积分。

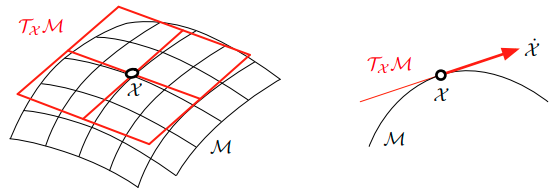
manifold and tangent space

Fig. 2: 一个流形 $\mathcal M$ 和向量空间 $T_\mathcal X \mathcal M$ (在本例中 $\cong \mathbb R^2$ ) 相切于点 $\mathcal X$ ，且是一个方便的侧切。速度元素 $\dot{\mathcal X} = \partial \mathcal X / \partial t$ 不属于流形 $\mathcal M$ ，而是属于切空间 $T_\mathcal X \mathcal M$

另一方面，$group (\mathcal G, \circ)$ 是一个具有组合操作 $\circ$ 的集合 $\mathcal G$ ，对于元素 $\mathcal{X, Y,Z} \in \mathcal G$ ，满足以下公理： $$ \begin{align*} \text{封闭性 (Closure under) ‘} \circ \text{’} \ &: \quad \mathcal X \circ \mathcal Y \in \mathcal G \tag{1.1.a} \label{1.1.a} \newline \text{幺元 (Identity) } \mathcal E \ &: \quad \mathcal E \circ \mathcal X = \mathcal X \circ \mathcal E = \mathcal X \tag{1.1.b} \label{1.1.b} \newline \text{逆 (Inverse) } \mathcal X^{-1} \ &: \quad \mathcal X^{-1} \circ \mathcal X = \mathcal X \circ \mathcal X^{-1} = \mathcal E \tag{1.1.c} \label{1.1.c} \newline \text{结合律 (Associativity) } \ &: \quad (\mathcal X \circ \mathcal Y) \circ \mathcal Z = \mathcal X \circ (\mathcal Y \circ \mathcal Z) \tag{1.1.d} \label{1.1.d} \end{align*} $$ 在李群中，流形在每一点上看起来都是一样的（比如在球体的表面，见 Ex. 1 和 Ex. 2 ），因此在任何一点上的所有切空间都是相似的。群结构要求流形元素的组成保持在流形上 $\eqref{1.1.a}$ ，并且每个元素在流形中也有一个逆 $\eqref{1.1.c}$ 。这些元素中的一个特殊元素是幺元 $\eqref{1.1.b}$ ，因此切线空间中的一个特殊元素是在幺元处的切线，我们称之为李群的李代数。李群将光滑流形的局部属性 (使能够进行微积分) 与群的全局属性结合起来，使远处物体的非线性组合成为可能。

Example 1: 单位复数群 (The unit complex numbers group) $S^1$
第一个最容易形象化李群的例子是复数乘法下的单位复数群 (见 Fig. 3) 。单位复数的形式是 ${\bf z} = \cos \theta + i \sin \theta$ 。
作用：向量 ${\mathbf x} = x + iy$ 在平面上旋转了一个角度 $\theta$ ，通过复数乘法，${\bf x}’ = {\bf zx}$
群事实：单位复数的乘积是单位复数，幺元为 1，逆是共轭 ${\bf z}^*$
流形事实：单位范数约束定义了复平面中的单位圆（可以看作是 1-sphere，因此被称为 $S^1$）。这是在二维空间中的一个 1-DoF 曲线。单位复数在这个圆上随时间演化。该群（圆）与线性空间（切线）局部相似，但不是全局相似。

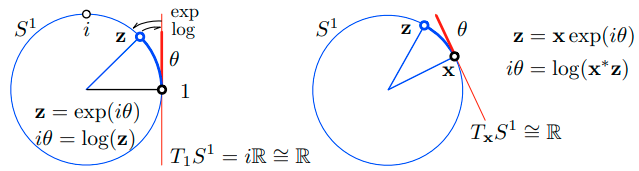
The S^1 manifold

Fig. 3: $S^1$ 流形是平面 $\mathbb C$ 中的单位圆（蓝色），存在单位复数 ${\bf z}^* {\bf z} = 1$ 。李代数 $\mathfrak s^1 = T_\mathcal E S^1$ 是虚数 $i\mathbb R$ 的线（红色），任何切线空间 $TS^1$ 都与线 $\mathbb R$ （红色）同构。切线向量（红色段）包裹流形，形成圆弧（蓝色弧）。映射 $\exp$ 和 $\log$ （箭头）将 $i\mathbb R$ 的元素映射（环绕和展开 (wrap and unwrap)）到 $S^1$ 的元素或从 $S^1$ 的元素（蓝色弧）映射。单位复数之间的增量通过组合和指数映射在切线空间中表示（我们将为此定义特殊的运算符 $\oplus, \ominus$）。有关解释，请参见文本，对于类似的群，请参见 Fig. 4 。

Example 2: 单位四元数群 (The unit quaternions group) $S^3$
李群的第二个例子也是相对容易形象化的四元数乘法下的单位四元数群 (见 Fig. 4) 。单位四元数的形式是 ${\bf q} = \cos(\theta/2) + {\bf u}\sin(\theta/2)$ ，其中 ${\bf u} = i u_x + j u_y + k u_z$ 为单位轴，$\theta$ 为旋转角。
作用：向量 ${\bf x} = ix+jy+kz$ 在三维空间中通过双四元乘积 ${\bf x}’ = {\bf qxq}^*$ 围绕单位轴 $\bf u$ 旋转了角度 $\theta$
群事实：单位四元数的乘积是单位四元数，幺元为 1，逆是共轭四元数 ${\bf q}^*$
流形事实：单位范数约束定义了 3-sphere $S^3$ ，球状的 3 维表面或 4 维空间的流形。单位四元数在这个表面上随时间演化。群（球体）与线性空间（切向超平面 $\mathbb R^3 \subset \mathbb R^4$ ）局部相似，但不是全局相似。

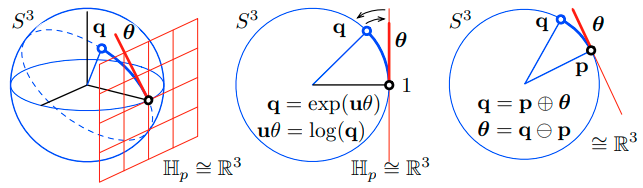
The S^3 manifold

Fig. 4: $S^3$ 流形是四元数 $\mathbb H$ 的 4-space 中单位 3-sphere （蓝色），其中存在单位四元数 ${\bf q}^* {\bf q} = 1$ 。李代数是纯虚四元数空间 $ix+jy+kz \in \mathbb H_p$ ，与超平面 $\mathbb R^3$ （红色网格）同构，任何其他切线空间 $TS^3$ 也与 $\mathbb R^3$ 同构。切线向量（红色线段）将流形包裹在大弧或测地线（虚线）上。中间图和右图显示了同构测地线的一个侧切（注意它与 Fig. 3 中的 $S^1$ 很相似）。映射 $\exp$ 和 $\log$ （箭头）将 $\mathbb H_p$ 的元素映射（包裹和展开）到/从 $S^3$ 的元素（蓝弧）。四元数之间的增量在切线空间通过运算符 $\oplus, \ominus$ 表示。

1.2 群运算 - The group actions

李群重要的是具有转换其他集合元素的能力，例如产生旋转、平移、缩放和它们的组合。这些都被广泛用于机器人技术，包括在二维和三维空间。给定一个李群 $\mathcal M$ 和一个集合 $\mathcal V$ ，其中有 $\mathcal X \in \mathcal M$ 对 $v\in \mathcal V$ 的运算 $\mathcal X \cdot v$ 定义如下： $$ \cdot \ : \ \mathcal M \times \mathcal V \to \mathcal V \ ; \ (\mathcal X, v) \mapsto \mathcal X \cdot v \tag{1.2} \label{1.2} $$ 要使 $\cdot$ 成为群运算，它必须满足以下公理： $$ \begin{align*} \text{幺元 (Identity) } \ &: \quad \mathcal E \circ \mathcal X = \mathcal X \circ \mathcal E = \mathcal X \tag{1.3.b} \label{1.3.a} \newline \text{兼容性 (Compatibility) } \ &: \quad (\mathcal X \circ \mathcal Y) \cdot v = \mathcal X \cdot (\mathcal Y \cdot v) \tag{1.3.d} \label{1.3.b} \end{align*} $$ 常见的例子有旋转矩阵群 $SO(n)$ ，单位四元数群，以及刚性运动群 $SE(n)$ 。它们各自对向量的作用满足： $$ \begin{align*} SO(n) \ &: \text{rotation matrix} & {\bf R} \cdot {\bf x} &\triangleq {\bf R x} \tag{1.4.a} \label{1.4.a} \newline SE(n) \ &: \text{Euclidean matrix} & {\bf H} \cdot {\bf x} &\triangleq {\bf R x} + {\bf t} \tag{1.4.b} \label{1.4.b} \newline S^1 \ &: \text{unit complex} & {\bf z} \cdot {\bf x} &\triangleq {\bf zx} \tag{1.4.c} \label{1.4.c} \newline S^3 \ &: \text{unit quaternion} & {\bf q} \cdot {\bf x} &\triangleq {\bf qxq}^* \tag{1.4.d} \label{1.4.d} \end{align*} $$ 更详细的阐述见 Table 1，以及附录中的内容。群的组合 $\eqref{1.1.a}$ 可以被看作是群对自身的运算，即 $\circ：\mathcal M \times \mathcal M \to \mathcal M$ 。另一个有趣的作用是伴随运算 (adjoint action)，我们将在 1.6 节中介绍。

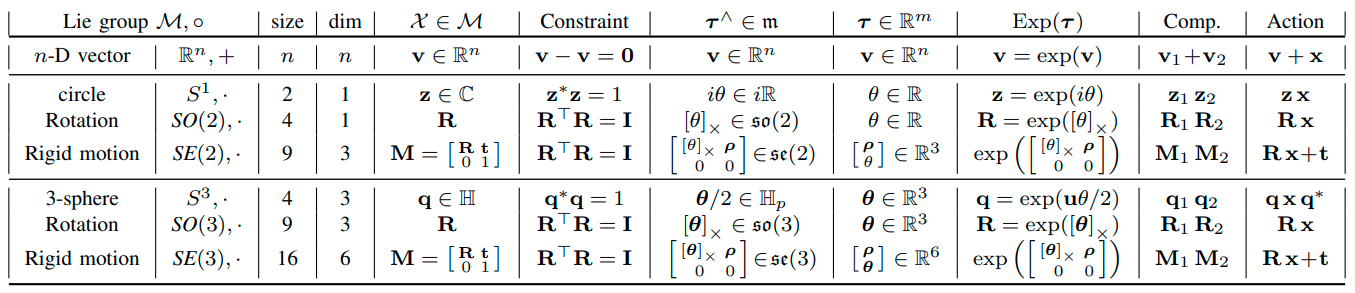
group actions

Tabel 1: 2D 和 3D 运动中使用的典型李群，包括平凡的 $\mathbb R^n$ 。请参阅附录以获取完整参考或¹ 中 [Lie theory cheat sheet] 。

1.3 切线空间和李代数 - The tangent spaces and the Lie algebra

设 $\mathcal X(t)$ 是一个在李群流形 $\mathcal M$ 上运动的点，其速度 $\dot{\mathcal X} = \partial \mathcal X / \partial t$ 属于在 $\mathcal X$ 处与 $\mathcal M$ 相切的空间（见 Fig. 2 ），记为 $T_\mathcal X \mathcal M$ 。流形的平滑性，即没有边缘或尖峰，意味着在每一点上存在一个唯一的切线空间。这种切线空间的结构处处相同。

1.3.1 李代数 $\mathfrak m$

幺元 $T_\mathcal E \mathcal M$ 处的切空间称为 $\mathcal M$ 的李代数，记为 $\mathfrak m$ ， $$ \text{Lie algebra : } \qquad \mathfrak m \triangleq T_\mathcal E \mathcal M \tag{1.5}\label{1.5} $$ 每个李群都有一个关联的李代数。我们通过以下事实⁶将李群与其李代数联系起来（见 Fig. 1 和 Fig. 6 ）：

李代数 $\mathfrak m$ 是一个向量空间。因此，它的元素可以与 $\mathbb R^m$ 中的向量相对应，其维数 $m$ 是 $\mathcal M$ 的自由度数
指数映射 (exponential map) ，$\exp: \mathfrak m \to \mathcal M$ 正好将李代数的元素转换成群的元素。对数映射是逆运算
$\mathcal X$ 处的切空间向量可以通过线性变换变换到幺元 $\mathcal E$ 处的切空间。这种变换称为伴随变换 (adjoint) 。

可以在切点 $\mathcal X$ 的局部范围内定义李代数，从而建立 $T\mathcal{_X M}$ 的局部坐标系 (Fig. 5) 。将采用 ‘hat’ 修饰符来表示李代数的元素，例如 $\bf v^\wedge$ 表示速度或 ${\boldsymbol \tau}^\wedge = ({\bf v}t)^\wedge = {\bf v}^\wedge t$ 表示一般元素。还可以添加左上标来制定精确的切线空间，例如 $^{\mathcal X}{\bf v}^\wedge \in T \mathcal{_X M}$ 和 $^{\mathcal E}{\bf v}^\wedge \in T \mathcal{_E M}$ 。

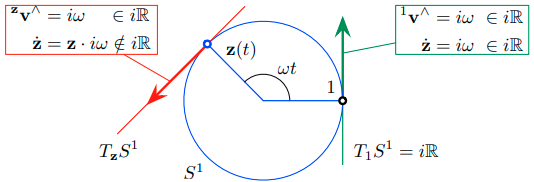
tangent spaces

Fig. 5 : 设点 ${\bf z}\in S^1$ 以恒定的旋转速率 $\omega$ 运动，${\bf z}(t) = \cos\omega t + i \sin\omega t$ 。它通过 $1$ 和 $\bf z$ 时的速度分别位于各自的切线空间 $T_1S^1$ 和 $T_\mathbf z S^1$ 中。在 $T_\mathbf z S^1$ 的情况下，速度用全局坐标系表示为 $\dot {\bf z} = {\bf z} i \omega = -\omega \sin \omega t + i\omega \cos \omega t$ ，用局部坐标系表示为 $^{\bf z}{\bf v}^\wedge = i\omega$ 。它们之间的关系为 $^{\bf z}{\bf v}^\wedge = {\bf z}^{-1} \dot{\bf z} = {\bf z}^*\dot{\bf z}$ 。在 $T_1S^1$ 的情况下，该关系就是幺元等式 $^1{\bf v}^\wedge = \dot{\bf z} = i\omega$ 。显然，所有切空间的结构都是 $i\mathbb R$ ，也就是李代数。这也是 $\dot{\bf z}$ 位于幺元处的结构，这就是为什么李代数被定义为幺元处的切空间。

通过对群约束条件 $\eqref{1.1.c}$ 进行时间微分，可以找到李代数的结构（参见示 Ex. 3 和 Ex. 5 ）。对于乘法群，这将产生新的约束 $\mathcal X^{-1} \dot{\mathcal X} + \dot{\mathcal X}^{-1} \mathcal X = 0$ ，它适用于与 $\mathcal X$ 相切的元素（项 $\dot{\mathcal X}^{-1}$ 是逆的导数）。因此李代数的元素形式为（对于加性李群，约束 $\mathcal{X - X} = 0$ 微分为 $\dot{\mathcal X} = \dot{\mathcal X}$ ，也就是说，没有任何约束会影响切空间。这意味着切空间与群空间相同。详见附录 E）： $$ {\bf v}^\wedge = \mathcal{X}^{-1} \dot{\mathcal X} = - \dot{\mathcal X}^{-1} {\mathcal X} \tag{1.6} \label{1.6} $$

Example 3: 旋转群 $SO(3)$ ，与其李代数 $\mathfrak{so}(3)$ 和向量空间 $\mathbb R^3$
在旋转群 $SO(3)$ 中，$3\times3$ 旋转矩阵 $\bf R$ 具有正交条件 ${\bf R^\top R} = \bf I$ 。可以通过对该约束求时间导数来找到切空间 ${\bf R}^\top \dot{\bf R} + \dot{\bf R}^\top {\bf R} = 0$ ，即将其重新排列为
$$ {\bf R}^\top \dot{\bf R} = - \dot{\bf R}^\top {\bf R} $$
该表达式揭示了 ${\bf R}^\top \dot{\bf R}$ 是一个倾斜对称矩阵（矩阵的转置为其负值）。斜对称矩阵通常被称为 $[\omega]_\times$，其形式为
$$ [\boldsymbol\omega]_\times = \begin{bmatrix} 0 & -\omega_z & \omega_y \newline \omega_z & 0 & -\omega_x \newline -\omega_y & \omega_x & 0 \end{bmatrix} $$
设 ${\bf R}^\top \dot{\bf R} = [\boldsymbol\omega]_\times$ ，则当 $\bf{R} = \bf{I}$ 时有
$$ \dot{\bf R} = [\boldsymbol\omega]_\times $$
也就是说，$[\boldsymbol\omega] _\times$ 属于 $SO(3)$ 的李代数，将其命名为 $\mathfrak{so}(3)$ 。由于 $[\boldsymbol\omega] _\times \in \mathfrak{so}(3)$ 有 3 个自由度 (DoF) ，所以 $SO(3)$ 的维数为 $m = 3$ 。李代数是一个向量空间，其元素可以分解为
$$ [\boldsymbol\omega]_\times = \omega_x {\bf E}_x + \omega_y {\bf E}_y + \omega_z {\bf E}_z $$
其中 ${\bf E}_x = \begin{bmatrix} 0 & 0 & 0 \newline 0 & 0 & -1 \newline 0 & 1 & 0 \end{bmatrix}, {\bf E}_y = \begin{bmatrix} 0 & 0 & 1 \newline 0 & 0 & 0 \newline -1 & 0 & 0 \end{bmatrix}, {\bf E}_z = \begin{bmatrix} 0 & -1 & 0 \newline 1 & 0 & 0 \newline 0 & 0 & 0 \end{bmatrix}$ 是 $\mathfrak{so}(3)$ 的生成器，其中 $\boldsymbol \omega = (\omega_x, \omega_y, \omega_z) \in \mathbb R^3$ 是角速度向量。根据上述一一对应的线性关系，可以将 $\mathfrak{so}(3)$ 与 $\mathbb R^3$ 相提并论，即写成 $\mathfrak{so}(3) \cong \mathbb R^3$ 。使用线性运算符 hat 和 vee 在 $\mathfrak{so}(3)$ 与 $\mathbb R^3$ 之间互相变换，
$$ \begin{align*} &{\rm Hat}: & \mathbb R^3 &\to \mathfrak{so}(3) & \boldsymbol\omega &\mapsto \boldsymbol\omega^\wedge = [\boldsymbol\omega] _\times \newline &{\rm Vee}: & \mathfrak{so}(3) &\to \mathbb R^3 & [\boldsymbol\omega] _\times &\mapsto [\boldsymbol\omega] _\times^\vee = \boldsymbol\omega \end{align*} $$

1.3.2 笛卡尔向量空间 $\mathbb R^m$

李代数的元素 $\boldsymbol \tau^\wedge$ 具有非第一的结构（斜对称矩阵、虚数、纯四元数，见 Table 1），但对我们来说，关键的一点是它们可以表示为一些基本元素 $E_i$ 的线性组合，其中 $E_i$ 被称为 $\mathfrak m$ 的生成器（它们是 $\mathcal X$ 在第 $i$ 个方向上绕原点的导数）。因此，只需将 $\mathbb R^m$ 中的向量进行坐标操作处理即可，将简称为 $\boldsymbol \tau$ 。可以通过两个相互逆的线性映射或同构 (isomorphisms) ，从 $\mathfrak m$ 传递到 $\mathbb R^m$ ，反之亦然，通常称为 hat 和 vee（见 Fig. 6 ）， $$ \begin{align*} &{\rm Hat}: & \mathbb R^m &\to \mathfrak{m} & \boldsymbol\tau &\mapsto \boldsymbol\tau^\wedge = \sum_{i=1}^m \tau_i E_i \tag{1.7.a} \label{1.7.a} \newline &{\rm Vee}: & \mathfrak{m} &\to \mathbb R^m & \boldsymbol\tau^\wedge &\mapsto (\boldsymbol\tau^\wedge)^\vee = \boldsymbol\tau = \sum_{i=1}^m \tau_i {\bf e}_i \tag{1.7.b} \label{1.7.b} \end{align*} $$ 其中 ${\bf e}_i$ 为 $\mathbb R^m$ 的基向量（有 ${\bf e}_i^\wedge = E_i$ ）。这意味着 $\mathfrak m$ 与向量空间 $\mathbb R^m$ 同构可以写成 $\mathfrak m \cong \mathbb R^m$ 或 $\boldsymbol \tau^\wedge \cong \boldsymbol \tau$ 。与同构的 $\boldsymbol \tau \in \mathfrak m$ 相比， $\boldsymbol \tau \in \mathbb R^m$ 对我们来说更方便，因为它们可以堆叠在更大的状态向量中，更重要的是，它们可以用矩阵算子进行线性代数运算。在本研究中，强制执行 $\mathbb R^m$ 优先于 $\mathfrak m$ 的原则偏好，以至于定义的大多数算子和对象（特别是：伴随矩阵、雅可比矩阵、扰动及其协方差矩阵）都在 $\mathbb R^m$ 上。

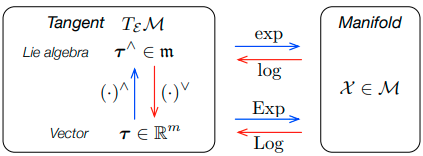
linear maps

Fig. 6: 流形 $\mathcal M$ 与其在原点 $T\mathcal{_E M}$ 处的切空间之间的映射表示。映射 ${\rm hat}(\cdot)^\wedge$ 和 ${\rm vee}(\cdot)^\vee$ 是现行可逆映射或同构映射 $\eqref{1.7.a} \eqref{1.7.b}$ ，$\exp(\cdot)$ 和 $\log(\cdot)$ 把李代数映射到了流形或从流形映射到李代数，${\rm Exp}(\cdot)$ 和 ${\rm Log}(\cdot)$ 是直接把向量空间 $\mathbb R^m$ 映射到了 $\mathcal M$ 或从 $\mathcal M$ 映射到 $\mathbb R^m$ 的快捷方式。

1.4 指数映射 - The exponential map

指数映射 $\exp()$ 使能够将李代数的元素精确地转移到群中 (Fig. 1) ，这种操作通常称为回缩 (retraction) 。直观上， $\exp()$ 沿着大弧或测地线将切线元素包裹在流形上（就像将绳子缠绕在球上一样，Fig. 1、Fig. 3、Fig. 4）。逆映射是 $\log()$ ，即展开操作。通过考虑流形上 $\mathcal X \in \mathcal M$ 的时间导数， $\exp()$ 映射自然产生，如下所示。从 $\eqref{1.6}$ 可以得出 $$ \dot{\mathcal X} = \mathcal X \bf v^\wedge \tag{1.8} \label{1.8} $$ 对于常数 $\bf v$ ，这是一个常微分方程 (ordinary differential equation, ODE) ，其解为 $$ \mathcal X (t) = \mathcal X(0) \exp( {\bf v}^\wedge t) \tag{1.9} \label{1.9} $$ 由于 $\mathcal X(t)$ 和 $\mathcal X(0)$ 是群中的元素，那么 $\exp({\bf v}^\wedge t) = \mathcal X(0)^{-1} \mathcal X(t)$ 也一定在群中，因此 $\exp({\bf v}^\wedge t)$ 将李代数中的元素 ${\bf v}^\wedge t$ 映射到群中。这就是所谓的指数映射。为了提供指数映射的更通用的定义，让我们将切线增量 $\boldsymbol \tau \triangleq {\bf v} t \in \mathbb R^m$ 定义为单位时间的速度，这样就有了李代数中的一个点 $\boldsymbol\tau^\wedge = {\bf v}^\wedge t \in \mathfrak m$ 。指数映射及其逆对数映射现在可以写为 $$ \begin{align*} \exp &: & \mathfrak m &\to \mathcal M & \boldsymbol\tau^\wedge &\mapsto \mathcal X = \exp(\boldsymbol\tau^\wedge) \tag{1.10.a} \label{1.10.a} \newline \log &: & \mathcal M &\to \mathfrak m & \mathcal X &\mapsto \boldsymbol\tau^\wedge = \log(\mathcal X) \tag{1.10.b} \label{1.10.b} \end{align*} $$ 通过写出绝对收敛的泰勒级数，可以得到乘法群中指数的封闭形式 (Closed forms ) $$ \exp (\boldsymbol\tau^\wedge) = \mathcal E + \boldsymbol\tau^\wedge + \frac12\boldsymbol\tau^{\wedge2} + \frac1{3!}\boldsymbol\tau^{\wedge3} + \cdots \tag{1.11} \label{1.11} $$ 并利用 $\boldsymbol\tau^\wedge$ 幂的代数性质（有关 $SO(3)$ 和 $S^3$ 中的指数映射推导，请参见 Ex. 4 和 EX. 5）。然后将其反转，就能找到对数映射。指数映射的主要性质如下： $$ \begin{align*} \exp((t+s)\boldsymbol\tau^\wedge) &= \exp(t\boldsymbol\tau^\wedge) \exp(s\boldsymbol\tau^\wedge) \tag{1.12.a} \label{1.12.a} \newline \exp(t\boldsymbol\tau^\wedge) &= \exp(\boldsymbol\tau^\wedge)^t \tag{1.12.b}\label{1.12.b} \newline \exp(-\boldsymbol\tau^\wedge) &= \exp(\boldsymbol\tau^\wedge)^{-1} \tag{1.12.c}\label{1.12.c} \newline \exp(\mathcal X \boldsymbol\tau^\wedge \mathcal X^{-1}) &= \mathcal X \exp(\boldsymbol\tau^\wedge) \mathcal X^{-1} \tag{1.12.d}\label{1.12.d} \end{align*} $$ 其中 $\eqref{1.12.d}$ 是一个令人惊讶且有力的陈述，可以通过展开泰勒级数并简化许多项 $\mathcal X^{−1} \mathcal X$ 来轻松证明。

1.4.1 大写的指数映射 - The capitalized exponential map

大写的 $\rm Exp$ 和 $\rm Log$ 映射是直接将向量元素 $\boldsymbol\tau \in \mathbb R^m (\cong T\mathcal{_E M})$ 与元素 $\mathcal{X \in M}$ 之间直接映射的便捷方式，有

$$ \begin{align*} {\rm Exp} &: & \mathbb R^m &\to \mathcal M & \boldsymbol\tau &\mapsto \mathcal X = {\rm Exp}(\boldsymbol\tau) \tag{1.13.a} \label{1.13.a} \newline {\rm Log} &: & \mathcal M &\to \mathbb R^m & \mathcal X &\mapsto \boldsymbol\tau = {\rm Log}(\mathcal X) \tag{1.13.b} \label{1.13.b} \end{align*} $$ 从 Fig. 6 中可以明显看出 $$ \begin{align*} \mathcal X &= {\rm Exp} (\boldsymbol\tau) \triangleq \exp(\boldsymbol\tau^\wedge) \tag{1.14.a} \label{1.14.a} \newline \boldsymbol\tau &= {\rm Log}(\mathcal X) \triangleq \log(\mathcal X)^\vee \tag{1.14.b} \label{1.14.b} \end{align*} $$ 有关不同流形的这些映射的实现的详细信息，请参阅附录。

Example 4: 关于 $SO(3)$ 的指数映射
在 Ex. 3 中的 $\dot {\bf R} = {\bf R}[\boldsymbol\omega] _\times \in T _\mathbf R SO(3)$ 。对于常数 $\boldsymbol\omega$ ，这是一个常微分方程，其解为 $\mathbf R (t) = \mathbf R_0 \exp([\boldsymbol\omega] _\times t)$ 。在原点 $\mathbf R_0 = \bf I$ 处有指数映射，
$$ \mathbf R(t) = \exp( [\boldsymbol\omega]_\times t) \qquad \in SO(3) $$
现在将定义向量 $\boldsymbol\theta \triangleq \mathbf u \theta \triangleq \boldsymbol\omega t \in \mathbb R^3$ 为绕单位轴 $\bf u$ 旋转角度 $\theta$ 的积分旋转，因此 $[\boldsymbol\theta ]_\times \in \mathfrak{so}(3)$ 是用李代数表示的总旋转。将其带入上文的内容，然后将指数写成幂级数，
$$ \mathbf R = \exp([\boldsymbol\theta] _\times) = \sum_k \frac{\theta^k}{k!} ([\mathbf u] _\times)^k $$
为了找到封闭式表达式，写下 $[\mathbf u] _\times$ 的几个幂，
$$ \begin{align*} [\mathbf u] _\times^0 &= \mathbf I & [\mathbf u] _\times^1 &= [\mathbf u] _\times \newline [\mathbf u] _\times^2 &= {\bf uu}^\top - \mathbf u & [\mathbf u] _\times^3 &= - [\mathbf u] _\times \newline [\mathbf u] _\times^4 &= - [\mathbf u] _\times^2 & &\cdots \end{align*} $$
并意识到它们都可以表示为 $\bf I$ 、 $[\mathbf u] _\times$ 或 $[\mathbf u] _\times^2$ 的倍数。因此，将数列改写为
$$ \begin{align*} \mathbf R = \mathbf I &+ [\mathbf u]_\times (\theta - \frac1{3!}\theta^3 + \frac1{5!}\theta^5 - \cdots) \newline &+ [\mathbf u] _\times^2 (\frac12\theta^2 - \frac1{4!}\theta^4 + \frac1{6!}\theta^6 - \cdots) \end{align*} $$
其中，根据 $\sin \theta$ 和 $\cos \theta$ 的泰勒展开序列，得出闭式解
$$ \mathbf R = \exp([\mathbf u \theta] _\times) = \mathbf I + [\mathbf u] _\times \sin\theta + [\mathbf u] _\times^2 (1-\cos\theta) $$
这个表达式就是众所周知的罗德里格斯旋转公式 (Rodrigues rotation formula) 。只需执行 $R = {\rm Exp}(\mathbf u \theta) = \exp([\mathbf u \theta] _\times)$ 即可将其用作大写指数。

Example 5: 单位四元数群 (The unit quaternions group) $S^3$ (Ex. 2 续)
在群 $S^3$ 中（回顾 Ex. 2 并参见 ⁹），根据单位规范条件 $\mathbf q^* \mathbf q = 1$ ，它的时间导数为 $$ \mathbf q^* \dot{\mathbf q} = -(\mathbf q^* \dot{\mathbf q})^* $$ 这表明 $\mathbf q^* \dot{\mathbf q}$ 是纯四元数（其实部为零）。纯四元数 $\mathbf uv \in \mathbb H_p$ 具有一下形式 $$ \mathbf uv = (i u_x + j u_y + k u_z)v = i v_x + j v_y + k v_z $$ 其中，$\mathbf u \triangleq i u_x + j u_y + k u_z$ 是单位纯虚向量，$v$ 是范数，$i,j,k$ 是李代数 $\mathfrak s^3 = \mathbb H_p$ 的生成元。对上述条件进行重写，可得 $$ \dot{\bf q} = \mathbf{q \ u}v \qquad \in T_\mathbf q S^3 $$ 其积分为 $\mathbf q = \mathbf q_0 \exp({\bf u}vt)$ 。设 $\mathbf q_0 = 1$ 并定义 $\boldsymbol\phi \triangleq \mathbf u \phi \triangleq \mathbf u vt$ ，指数映射有 $$ \mathbf q = \exp(\mathbf u \phi) \triangleq \sum \frac{\phi^k}{k!} \mathbf u^k \qquad \in S^3 $$ $\mathbf u$ 的幂项依次为 $1, \mathbf u, -1, -\mathbf u, 1, \cdots$ 。因此，将 $1$ 和 $\mathbf u$ 中的项分组，并确定 $\cos \phi$ 和 $\sin \phi$ 的泰勒展开序列。得到封闭形式 $$ \mathbf q = \exp(\mathbf u \phi) = \cos(\phi) + \mathbf u \sin(\phi) $$ 这是欧拉公式 $\exp(i\phi) = \cos\phi + i \sin\phi$ 的完美扩展。李代数 $\boldsymbol \phi = \mathbf u\phi \in \mathfrak s^3$ 的元素可以通过 hat 和 vee 映射用旋转向量 $\boldsymbol\theta \in \mathbb R^3$ 来标识， $$ \begin{align*} {\rm Hat} &: & \mathbb R^3 &\to \mathfrak s^3 & \boldsymbol\theta &\mapsto \boldsymbol\theta^\wedge = \boldsymbol\theta/2 \newline {\rm Vee} &: & \mathfrak s^3 &\to \mathbb R^3 & \boldsymbol\phi &\mapsto \boldsymbol\phi^\vee = 2\boldsymbol\phi \end{align*} $$ 其中，因子 $2$ 表示四元素在旋转作用中的双重效应，即 $\mathbf x = {\bf q\ x\ q}^*$ 。伴随 Hat 和 Vee 的操作，四元数指数映射 $$ \mathbf q = {\rm Exp}(\mathbf u\theta) = \cos(\theta/2) + \mathbf u \sin(\theta/2) $$ 等价于旋转矩阵 $\mathbf R = {\rm Exp}(\mathbf u \theta)$ 。

1.5 加减运算 - Plus and minus operators

加减运算允许在（弯曲 (curved) ）流形的元素之间引入增量，并在其（平坦 (flat) ）切向量空间中表示它们。用 $\oplus$ 和 $\ominus$ 表示，它们结合了一个 $\rm Exp/Log$ 运算和一个组合运算。由于组合的非交换性，它们根据操作数的顺序被定义为右运算符和左运算符。右运算符为（见 Fig. 4-right） $$ \begin{align*} {\rm right-}\oplus &:& \mathcal Y &= \mathcal X \oplus {}^\mathcal X \boldsymbol\tau \triangleq \mathcal X \circ {\rm Exp}({}^\mathcal X \boldsymbol\tau) \in \mathcal M \tag{1.15.a} \label{1.15.a} \newline {\rm right-}\ominus &:& ^\mathcal E \boldsymbol\tau &= \mathcal Y \ominus \mathcal X \triangleq {\rm Log}(\mathcal X^{-1} \circ \mathcal Y) \in T \mathcal{_X M} \tag{1.15.b} \label{1.15.b} \end{align*} $$ 在 $\eqref{1.15.a}$ 中，${\rm Exp}(^\mathcal X \boldsymbol\tau)$ 出现在组合的右侧，因此 $^\mathcal X \boldsymbol\tau$ 属于 $\mathcal X$ 处的切空间（参见 $\eqref{1.15.b}$ ）：按照惯例（这一约定与坐标变换的约定相同，例如 $^G \mathbf x = \mathbf R {}^L\mathbf x$，其中矩阵 $R \in SO(3)$ 将局部向量变换为全局向量。需要注意的是，并非所有作者都认同这一约定，有的使用了相反的约定，即 $^L\mathbf x = \mathbf R {}^G \mathbf x$ ），说 $^\mathcal X \boldsymbol\tau$ 是在 $\mathcal X$ 处的局部坐标系中的表示 – 用左上标来表示参考系。左操作有， $$ \begin{align*} {\rm left-}\oplus &:& \mathcal Y &= {}^\mathcal E \boldsymbol\tau \oplus \mathcal X \triangleq {\rm Exp}({}^\mathcal E \boldsymbol\tau) \circ \mathcal X \in \mathcal M \tag{1.16.a} \label{1.16.a} \newline {\rm left-}\ominus &:& ^\mathcal E \boldsymbol\tau &= \mathcal Y \ominus \mathcal X \triangleq {\rm Log}(\mathcal Y^{-1} \circ \mathcal X) \in T \mathcal{_E M} \tag{1.16.b} \label{1.16.b} \end{align*} $$ 现在，在 $\eqref{1.16.a}$ 中 ${\rm Exp}(^\mathcal E \boldsymbol\tau)$ 位于左侧，并且有 $^\mathcal E \boldsymbol\tau \in T \mathcal{_E M}$ ：说 $^\mathcal E \boldsymbol\tau$ 是全局坐标系中的表示。

请注意，虽然 left- 和 right- $\oplus$ 可以按操作数顺序区分，但 $\eqref{1.15.b}$ 和 $\eqref{1.16.b}$ 中的 $\ominus$ 却含糊不清。在本文中，默认在局部表达扰动，因此默认使用 right- 形式的 $\oplus$ 和 $\ominus$ 。

1.6 伴随及伴随矩阵 - The adjoint, and the adjoint matrix

如果根据式 $\eqref{1.15.a}$ 和 $\eqref{1.16.a}$ 确立了 $\mathcal Y$ ，就会得出 ${}^\mathcal E \boldsymbol\tau \oplus \mathcal X = \mathcal X \oplus {}^\mathcal X \boldsymbol\tau$ ，这决定了局部和全局切元素之间的关系 (Fig. 7) 。将其与 $\eqref{1.12.d}\eqref{1.15.a} \eqref{1.16.a}$ 联立得， $$ \begin{align*} {\rm Exp}(^\mathcal E\boldsymbol \tau) \mathcal X &= \mathcal X {\rm Exp}(^\mathcal X\boldsymbol \tau) \newline \exp(^\mathcal E\boldsymbol \tau^\wedge) &= \mathcal X \exp(^\mathcal X\boldsymbol \tau^\wedge) \mathcal X^{-1} = \exp(\mathcal X ^\mathcal X\boldsymbol \tau^\wedge \mathcal X^{-1}) \newline ^\mathcal E\boldsymbol \tau^\wedge &= \mathcal X ^\mathcal X\boldsymbol \tau^\wedge \mathcal X^{-1} \end{align*} $$ 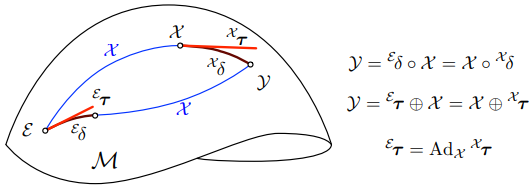two paths

Fig. 7: $\mathcal X \circ {}^\mathcal X\delta$ 和 $^\mathcal E\delta \circ \mathcal X$ 两条路径链接着原点 $\mathcal E$ 和点 $\mathcal Y$ 。它们分别用局部坐标系下 $^\mathcal X\delta$ 或原点坐标系下 $^\mathcal E\delta$ 表示的 deltas 增量与元素 $\mathcal X$ 组成。由于不可交换性，元素 $^\mathcal X\delta$ 和 $^\mathcal E\delta$ 并不相等。因此，它们的相关切向量 $^\mathcal X\boldsymbol\tau = {\rm Log}(^\mathcal X\delta)$ 和 $^\mathcal E\boldsymbol\tau = {\rm Log}(^\mathcal E\delta)$ 也不相等。它们通过线性变换 $^\mathcal E\boldsymbol\tau = \mathbf{Ad} _\mathcal X {}^\mathcal X \boldsymbol \tau$ 联系在一起，其中 $\mathbf{Ad} _\mathcal X$ 是 $\mathcal M$ 在 $\mathcal X$ 处的伴随。

1.6.1 伴随

因此，定义 $\mathcal M$ 在 $\mathcal X$ 处的伴随，记为 ${\rm Ad} _\mathcal X$ ，为 $$ {\rm Ad} _\mathcal X : \mathfrak m \to \mathfrak m \qquad \boldsymbol\tau^\wedge \mapsto {\rm Ad} _\mathcal X (\boldsymbol\tau^\wedge) \triangleq \mathcal X \boldsymbol\tau^\wedge \mathcal X^{-1} \tag{1.17} \label{1.17} $$ 所以有 $^\mathcal E\boldsymbol \tau^\wedge = {\rm Ad} _\mathcal X (^\mathcal X\boldsymbol \tau^\wedge)$ 。这定义了该群在其自身的李代数上的伴随作用。伴随作用有两个有趣（且易于证明）的性质， $$ \begin{align*} {\rm Linear} &:& {\rm Ad} _\mathcal X (a \boldsymbol\tau^\wedge + b \boldsymbol\sigma^\wedge) &= a{\rm Ad} _\mathcal X(\boldsymbol\tau^\wedge) + b {\rm Ad} _\mathcal X(\boldsymbol\sigma^\wedge) \newline {\rm Homomorphism} &:& {\rm Ad} _\mathcal X ({\rm Ad} _\mathcal Y (\boldsymbol\tau^\wedge)) &= {\rm Ad} _\mathcal{XY} (\boldsymbol\tau^\wedge) \end{align*} $$

1.6.2 伴随矩阵

由于 ${\rm Ad} _\mathcal X()$ 是线性的，因此可以找到一个等效矩阵算子 ${\bf Ad} _\mathcal X$ ，它可以映射笛卡尔切向量 $^\mathcal E \boldsymbol\tau \cong {}^\mathcal E \boldsymbol\tau^\wedge$ 和 $^\mathcal X \boldsymbol\tau \cong {}^\mathcal X \boldsymbol\tau^\wedge$ ， $$ {\bf Ad} _\mathcal X : \mathbb R^m \to \mathbb R^m \qquad ^\mathcal X \boldsymbol\tau \mapsto {}^\mathcal E \boldsymbol\tau = {\bf Ad} _\mathcal X {}^\mathcal X \boldsymbol\tau \tag{1.18} \label{1.18} $$ 我们称之为伴随矩阵。将 $^\vee$ 应用于 $\eqref{1.17}$ 即可计算出该矩阵，因此可以写成 $$ {\bf Ad} _\mathcal X \ \boldsymbol\tau = (\mathcal X \boldsymbol\tau^\wedge \mathcal X^{-1})^\vee \tag{1.19} \label{1.19} $$ 然后展开右边以确定伴随矩阵（参见 Ex. 6 和附录）。伴随矩阵的附加属性如下 $$ \begin{align*} \mathcal X \oplus \boldsymbol\tau &= ({\bf Ad} _\mathcal X \ \boldsymbol\tau) \oplus \mathcal X \tag{1.20.a} \label{1.20.a} \newline {\bf Ad} _\mathcal{X^{-1}} &= {\bf Ad} _\mathcal X {}^{-1} \tag{1.20.b} \label{1.20.b} \newline {\bf Ad} _\mathcal{XY} &= {\bf Ad} _\mathcal X {\bf Ad} _\mathcal Y \tag{1.20.c} \label{1.20.c} \end{align*} $$ 请注意在 $\eqref{1.20.b} \eqref{1.20.c}$ 中，等式的左边部分通常比右边部分更容易计算。经常使用伴随矩阵将 $\mathcal X$ 处的切空间向量线性变换到原点处的切空间向量，即 ${}^\mathcal E \boldsymbol\tau = {\bf Ad} _\mathcal X {}^\mathcal X \boldsymbol\tau$ 在本文中，伴随矩阵将简称为伴随。

Example 6: $SE(3)$ 的伴随矩阵
刚体运动的 $SE(3)$ 群（参见 App. D）具有群、李代数和向量元素，
$$ \mathbf M = \begin{bmatrix} \bf R & \bf t \newline \bf 0 & 1 \end{bmatrix} \qquad \boldsymbol \tau^\wedge = \begin{bmatrix} [\boldsymbol \theta]_\times & \boldsymbol \rho \newline \bf 0 & 0 \end{bmatrix} \qquad \boldsymbol \tau = \begin{bmatrix} \boldsymbol\rho \newline \boldsymbol\theta \end{bmatrix} $$
通过展开 $\eqref{1.19}$ 可以得到伴随矩阵为
$$ \begin{align*} {\bf Ad} _\mathbf M \ \boldsymbol \tau &= ({\bf M \boldsymbol\tau^\wedge M}^{-1})^\vee = \cdots = \newline &= \left( \begin{bmatrix} \bf R [\boldsymbol\theta] _\times R^\top & \bf R [\boldsymbol\theta] _\times R^\top t + R \boldsymbol\rho \newline \bf 0 & \bf 0 \end{bmatrix} \right)^\vee \newline &= \left( \begin{bmatrix} \bf [R\boldsymbol\theta] _\times & \bf [t] _\times R \boldsymbol\theta + R\boldsymbol\rho \newline \bf 0 & \bf 0 \end{bmatrix} \right)^\vee \newline &= \begin{bmatrix} \bf [t] _\times R \boldsymbol\theta + R\boldsymbol\rho \newline \bf R\boldsymbol\theta \end{bmatrix} = \begin{bmatrix} \bf R & \bf [t] _\times R \newline \bf 0 & \bf R \end{bmatrix} \begin{bmatrix} \boldsymbol\rho \newline \boldsymbol\theta \end{bmatrix} \end{align*} $$
其中，使用到变换公式 $[{\bf R}\boldsymbol\theta] _\times = \bf R[\boldsymbol\theta] _\times R^\top$ 和 $\mathbf{[a] _\times b} = -\mathbf{[b] _\times a}$ ，所以伴随矩阵为
$$ {\bf Ad_M} = \begin{bmatrix} \bf R & \bf [t]_\times R \newline \bf 0 & \bf R \end{bmatrix} \qquad \in \mathbb R^{6\times6} $$

1.7 李群的导数 - Derivatives on Lie groups

在李群背景下定义导数的各种方法中，我们主要关注以雅各布矩阵形式映射向量切空间的导数。这在本文中就足够了，因为在这些空间中，可以正确且轻松地定义不确定性和增量。使用这些雅各布矩阵后，李群中的不确定性管理公式将与矢量空间中的公式大体相似。下面描述的雅可比行列式满足链式法则，这样我们就可以很容易地从部分雅可比行列式的逆、组合、指数化和作用 (inversion, composition, exponentiation and action) 中计算任何雅可比行列式。有关详细信息和证明，请参阅第 III-A 节。

1.7.1 向量空间上的雅可比

对于多元函数 $f:\mathbb R^m \to \mathbb R^n$ ，雅可比矩阵定义为堆叠所有偏导数的 $n\times m$ 矩阵， $$ {\bf J} = \cfrac{\partial f(\mathbf x)}{\partial \mathbf x} \triangleq \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f1}{\partial x_m} \newline \vdots & & \vdots \newline \frac{\partial f_n}{\partial x_1} & \cdots & \frac{\partial f_n}{\partial x_m} \end{bmatrix} \in \mathbb R^{n\times m} \tag{1.21} \label{1.21} $$ 通过以下形式定义该矩阵很方便。让我们以 $\mathbf J = [\mathbf j_1 \cdots \mathbf j_m]$ 的形式进行划分，并让 $\mathbf j_i = [\frac{\partial f_1}{\partial x_i} \cdots \frac{\partial f_n}{\partial x_i}]^\top$ 为其第 $i$ 列向量。该列向量响应 $$ \mathbf j_i = \cfrac{\partial f(\mathbf x)}{\partial x_i} \triangleq \lim_{h \to 0} \cfrac{f(\mathbf x + h \mathbf e_i) - f(\mathbf x)}{h} \in \mathbb R^n \tag{1.22}\label{1.22} $$ 其中 $\mathbf e_i$ 是 $\mathbb R^m$ 自然基的第 $i$ 个向量。关于分子，请注意向量 $$ \mathbf v_i(h) \triangleq f(\mathbf x + h \mathbf e_i) - f(\mathbf x) \tag{1.23} \label{1.23} $$ 是当 $\bf x$ 在 $\mathbf e_i$ 方向上受到扰动时 $f(\mathbf x)$ 的变化，并且相应的雅可比列就是 $\mathbf j_i = \partial\mathbf v_i(h) / \partial h | _{h=0} = \lim _{h \to 0} \mathbf v_i(h)/h$ 。在本文中，为了方便起见，我们引入紧凑形式，

$$ \mathbf J = \cfrac{\partial f(\mathbf x)}{\partial \mathbf x} \triangleq \lim_{\mathbf h \to 0} \cfrac{f(\mathbf x + \mathbf h ) - f(\mathbf x)}{\mathbf h} \in \mathbb R^{n\times m} \tag{1.24}\label{1.24} $$

其中 $\mathbf h \in \mathbb R^m$ ，将所有列 $\eqref{1.22}$ 整合为 $\eqref{1.21}$ 的定义。我们要指出的是，$\eqref{1.24}$ 只是一种符号上的方便（正如 $\eqref{1.21}$ 一样），因为除以向量 $\bf h$ 是未定义的，正确的计算需要 $\eqref{1.22}$ 。不过，这种形式可以用来计算雅可比行列式，方法是将分子展开为 $\bf h$ 的线性形式，并左侧识别为雅可比行列式，即：

$$ \lim_{\mathbf h \to 0} \cfrac{f(\mathbf x + \mathbf h ) - f(\mathbf x)}{\mathbf h} = \cdots = \lim_{\mathbf h \to 0} \cfrac{\bf J h}{\bf J} \triangleq \cfrac{\partial \bf Jh}{\partial \bf h} = \bf J \tag{1.25}\label{1.25} $$ 最后注意，对于 $\bf h$ 的小值，我们可以得到线性近似值 $$ f(\mathbf x + \mathbf h) \xrightarrow[\mathbf h \to 0]{} f(\mathbf x) + \cfrac{\partial f(\mathbf x)}{\partial \mathbf x} \bf h \tag{1.26} \label{1.26} $$

1.7.2 李群上的右雅可比

受上面标准导数定义 $\eqref{1.24}$ 的启发，我们现在可以使用 $\oplus$ 和 $\ominus$ 算在来定义作用于流形的函数 $f:\mathcal M \to \mathcal N$ 的雅各比（见 Fig. 8 ）。使用 right-$\lbrace \oplus, \ominus \rbrace$ 替代 $\lbrace +, - \rbrace$ ，可以得到一种类似于标准导数的形式（在选择其他替代方案之前，使用符合 $\frac{D \mathcal Y}{D \mathcal X} = \frac{D f(\mathcal X)}{D \mathcal X}$ 为了使链式法则易读，即 $\frac{D \mathcal Z}{D \mathcal X} = \frac{D \mathcal Z}{D \mathcal Y} \frac{D \mathcal Y}{D \mathcal X}$。稍后将引入更简洁的符号 $\mathbf J^\mathcal Y _\mathcal X \triangleq \frac{D \mathcal Y}{D \mathcal X}$ ）

$$ \begin{align*} \cfrac{^\mathcal X Df(\mathcal X)}{D\mathcal X} &\triangleq \lim_{\boldsymbol\tau \to 0} \cfrac{f(\mathcal X \oplus \boldsymbol\tau) \ominus f(\mathcal X)}{\boldsymbol\tau} \qquad \in \mathbb R^{n\times m} \tag{1.27.a} \label{1.27.a} \newline &= \lim_{\boldsymbol\tau \to 0} \cfrac{{\rm Log} \big( f(\mathcal X)^{-1} \circ f(\mathcal X \circ {\rm Exp}(\boldsymbol \tau)) \big)}{\boldsymbol\tau} \tag{1.27.b} \label{1.27.b} \newline &= \left. \cfrac{\partial\ {\rm Log}\big( f(\mathcal X)^{-1} \circ f(\mathcal X \circ {\rm Exp}(\boldsymbol\tau)) \big)}{\partial \boldsymbol\tau} \right|_{\boldsymbol\tau = 0} \tag{1.27.c} \label{1.27.c} \end{align*} $$

我们称这个雅可比行列式为 $f$ 的右雅可比。注意 $\eqref{1.27.c}$ 只是想定复杂的函数 $g(\boldsymbol\tau) = {\rm Log}\big( f(\mathcal X)^{-1} \circ f(\mathcal X \circ {\rm Exp}(\boldsymbol\tau)) \big)$ 的标准导数 $\eqref{1.24}$ 。按 $\eqref{1.27.a}$ 的写法更直观：它是 $f(\mathcal X)$ 关于 $\mathcal X$ 的导数，只是我们表达了切空间中的无穷小变化。事实上，由于 right $\oplus$ 和 $\ominus$ 的运算方式， $\mathcal X$ 和 $f(\mathcal X)$ 的变化现在被表示为局部切线空间中的向量，即分别在 $\mathcal {X \in M}$ 和 $f(\mathcal X) \in \mathcal N$ 处切线。该导数是一个适当的雅可比矩阵 $\mathbb R^{n\times m}$ ，它线性地映射了局部切线空间 $T\mathcal {_X M} \to T _{f(\mathcal X )}\mathcal N$（我们用局部 ‘$\mathcal X$ ‘上标标记导数）。正如在向量空间中一样，该矩阵的列对应于方向导数。也就是说，向量

$$ \boldsymbol\sigma_i(h) = f(\mathcal X \oplus h \mathbf e_i) \ominus f(\mathcal X) \qquad \in \mathbb R^n \tag{1.28} \label{1.28} $$

（再次参见 Fig. 8 ，比较式 $\eqref{1.28}$ 中的 $\boldsymbol\sigma_i$ 与式 $\eqref{1.23}$ 中的 $\mathbf v_i$ ）是当 $\mathcal X$ 沿 $\mathbf e_i$ 方向变化时 $f(\mathcal X)$ 的变化量。其各自的雅可比列为 $\mathbf j_i = \partial \boldsymbol \sigma_i(h) / \partial h|_{h=0}$ 。

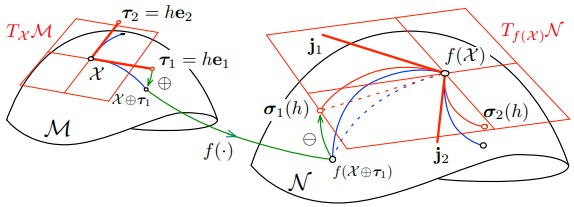
Right Jacobian

Fig. 8: 函数 $f:\mathcal M \to \mathcal N$ 的右雅可比行列式。正则方向上的扰动向量 $\boldsymbol\tau_i = h \mathbf e_i \in T\mathcal{_X M}$ 通过加、应用 $f()$ 和减（绿色箭头）的过程传播到扰动向量 $\boldsymbol\sigma_i \in T _{f(\mathcal X)} \mathcal N$ ，得到 $\boldsymbol\sigma_i(h) = f(\mathcal X \oplus h \mathbf e_i) \ominus f(\mathcal X)$ 。请注意在 $\mathcal M$ 中，$\boldsymbol \tau_i(h) = h \mathbf e_i$（红色粗线）的扰动会在 $\mathcal M$ （蓝色）中沿着测地线生成路径（回想 Fig. 1 ）。还要注意的是，在 $\mathcal N$ 中，由于 $f(\cdot)$ 的非线性，图像路径（蓝色实线）通常不在测地线（蓝色虚线）上。这些图像路径被提升 (lifted onto) 到切线空间 $T _{f(\mathcal X)} \mathcal N$ 上，产生平滑的曲线路径（红色细实线）。$\bf J$ 的列向量 $\mathbf j_i$（红色粗线）是在 $f(\mathcal X)$ 处求值的提升路径的导数，即 $\mathbf j_i = \lim _{h \to 0} \boldsymbol\sigma_i(h)/h$ 。每个 $h \mathbf e_i \in T\mathcal{_X M}$ 都有一个$\mathbf j_i \in T _{f(\mathcal X)} \mathcal N$ ，因此得到的雅可比矩阵 $\mathbf J = [\mathbf j_1 \cdots \mathbf j_m ] \in \mathbf R^{n\times m}$ 线性映射了从 $T\mathcal{_X M} \cong \mathbb R^m$ 到 $T _{f(\mathcal X)} \mathcal N \cong \mathbb R^n$ 的向量。

与之前一样，我们利用 $\eqref{1.27.a}$ 通过相同的机制 $\eqref{1.25}$ 来求得雅可比。例如，对于 3D 旋转 $f: SO(3) \to \mathbb R^3 \quad f(\mathbf R) = \bf Rp$ ，有 $\mathcal M = SO(3)$ 和 $\mathcal N = \mathbb R^3$ ，因此（参见 App. B-C5 ） $$ \begin{align*} \cfrac{^\mathbf R D \bf Rp}{\bf R} &= \lim _{\boldsymbol\theta \to 0} \cfrac{(\mathbf{R \oplus \boldsymbol\theta}) \mathbf{ p \ominus Rp}}{\boldsymbol\theta} = \lim _{\boldsymbol\theta \to 0} \cfrac{\mathbf R \ {\rm Exp}(\boldsymbol\theta) \mathbf p - \bf Rp}{\boldsymbol\theta} \newline &= \lim _{\boldsymbol\theta \to 0} \cfrac{\mathbf R (\mathbf I + [\boldsymbol\theta] _\times) \mathbf p - \bf Rp}{\boldsymbol\theta} = \lim _{\boldsymbol\theta \to 0} \cfrac{\bf R[\boldsymbol\theta] _\times p}{\boldsymbol\theta} \newline &= \lim _{\boldsymbol\theta \to 0} \cfrac{-\bf R[p] _\times \boldsymbol\theta}{\boldsymbol\theta} = -\mathbf{R[p] _\times} \qquad \in \mathbb R^{3\times3} \end{align*} $$

在第三节和附录中可以观察到这种机制的许多例子。需要注意的是，当函数 $f$ 从一个流形传递到另一个流形时，必须适当选择 $\eqref{1.27.a}$ 中的正负算子： $\oplus$ 针对域(domain) $\mathcal M$ ， $\ominus$ 针对目标域或像 (codomain or image) $\mathcal N$ 。对于较小的 $\boldsymbol \tau$ 值，以下近似成立

$$ f(\mathcal X \oplus {}^\mathcal X \boldsymbol\tau) \xrightarrow[^\mathcal X \boldsymbol\tau \to 0]{} f(\mathcal X) \oplus \cfrac{^\mathcal X Df(\mathcal X)}{D\mathcal X} {}^\mathcal X\boldsymbol\tau \qquad \in \mathcal N \tag{1.29} \label{1.29} $$

1.7.3 李群上的左雅可比

导数也可以由 left-$\lbrace \oplus, \ominus \rbrace$ 运算符定义，从而得出 $$ \begin{align*} \cfrac{^\mathcal E Df(\mathcal X)}{D\mathcal X} &\triangleq \lim_{\boldsymbol\tau \to 0} \cfrac{f(\boldsymbol\tau \oplus \mathcal X) \ominus f(\mathcal X)}{\boldsymbol\tau} \qquad \in \mathbb R^{n\times m} \tag{1.30} \label{1.30} \newline &= \lim_{\boldsymbol\tau \to 0} \cfrac{{\rm Log} \big(f( {\rm Exp}(\boldsymbol \tau) \circ \mathcal X) \circ f(\mathcal X)^{-1} \big)}{\boldsymbol\tau} \newline &= \left. \cfrac{\partial\ {\rm Log}\big( f({\rm Exp}(\boldsymbol\tau) \circ \mathcal X ) \circ f(\mathcal X)^{-1} \big)}{\partial \boldsymbol\tau} \right|_{\boldsymbol\tau = 0} \end{align*} $$ 我们称之为 $f$ 的左雅可比。请注意，现在 $\boldsymbol\tau \in T\mathcal{_E M}$ ，分子属于 $T\mathcal{_E N}$ ，因此左雅可比是映射全局切线空间 $T\mathcal {_E M} \to T \mathcal {_E N}$ 的 $n\times m$ 矩阵，它们是 $\mathcal M$ 和 $\mathcal N$ 的李代数（使用全局或原点上标 ‘$\mathcal E$ ‘标记导数）。对于较小的 $\boldsymbol \tau$ 值，以下公式成立： $$ f({}^\mathcal E \boldsymbol \tau \oplus \mathcal X) \xrightarrow[^\mathcal E \boldsymbol \tau \to 0]{} \cfrac{^\mathcal E Df(\cal X)}{D \cal X} {}^\mathcal E \boldsymbol \tau \oplus f(\mathcal X) \qquad \in \mathcal N \tag{1.31} \label{1.31} $$ 我们可以从 $\eqref{1.20.a} \eqref{1.29} \eqref{1.31}$ （见 Fig. 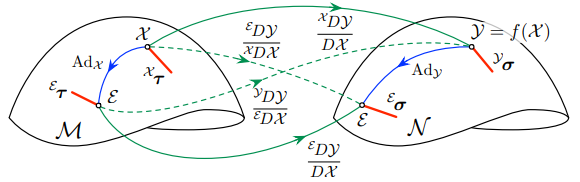9 ）证明左雅可比和右雅可通过 $\mathcal M$ 和 $\mathcal N$ 的伴随矩阵相关联的 $$ \cfrac{^\mathcal E Df(\cal X)}{D \cal X} \mathbf{Ad} _\mathcal X = \mathbf{Ad} _{f(\mathcal X)} \cfrac{^\mathcal X Df(\cal X)}{D \cal X} \tag{1.32} \label{1.32} $$ linear maps

Fig. 9: 函数 $\mathcal Y = f(\mathcal X)$ 中涉及的所有切空间之间的线性映射，从 $\mathcal M$ 到 $\mathcal N$ 。线性映射 $^\mathcal E \boldsymbol\tau = \mathbf{Ad} _\mathcal X {}^\mathcal X \boldsymbol\tau, \ ^\mathcal E \boldsymbol\sigma = \mathbf{Ad} _\mathcal Y {}^\mathcal Y \boldsymbol\sigma, \ ^\mathcal E \boldsymbol\sigma = \frac{^\mathcal E D \mathcal Y}{D\mathcal X} {}^\mathcal E \boldsymbol\tau$，以及 $^\mathcal Y \boldsymbol\sigma = \frac{^\mathcal X D \mathcal Y}{D\mathcal X} {}^\mathcal X \boldsymbol\tau$ ，形成一个环路（实线），从而得出 $\eqref{1.32}$ 。交叉的雅可比（虚线）形成更多的映射环路，则有 $\eqref{1.33.a} \eqref{1.33.b}$ 。

1.7.4 交叉右-左雅可比

还可以使用右加左减或相反的方法来定义雅可比。虽然不太可能，但有时也很有用，因为它们可以将局部切线映射到全局切线，反之亦然。为了简短起见，我们只需通过伴随关系将它们与其他雅可比函数联系起来 $$ \begin{alignat*}{2} \cfrac{^\mathcal E D \mathcal Y}{^\mathcal X D \mathcal X} &= \cfrac{^\mathcal E D \mathcal Y}{^\mathcal E D \mathcal X} \mathbf{Ad} _\mathcal X &&= \mathbf{Ad} _\mathcal Y \cfrac{^\mathcal Y D \mathcal Y}{^\mathcal X D \mathcal X} \tag{1.33.a} \label{1.33.a} \newline \cfrac{^\mathcal Y D \mathcal Y}{^\mathcal E D \mathcal X} &= \cfrac{^\mathcal Y D \mathcal Y}{^\mathcal X D \mathcal X} \mathbf{Ad} _\mathcal X {}^{-1} &&= \mathbf{Ad} _\mathcal Y {}^{-1} \cfrac{^\mathcal E D \mathcal Y}{^\mathcal E D \mathcal X} \tag{1.33.b} \label{1.33.b} \end{alignat*} $$ 其中 $\mathcal Y = f(\mathcal X)$ 。现在，上标和下标表示微分所在的参照系。相应的 small-tau 近似值为 $$ \begin{align*} f(\mathcal X \oplus {}^\mathcal X \boldsymbol\tau) &\xrightarrow[^\mathcal X \boldsymbol\tau \to 0]{} \cfrac{^\mathcal E Df(\mathcal X)}{^\mathcal X D\mathcal X} {}^\mathcal X\boldsymbol\tau \oplus f(\mathcal X) \tag{1.34.a} \label{1.34.a} \newline f({}^\mathcal E \boldsymbol \tau \oplus \mathcal X) &\xrightarrow[^\mathcal E \boldsymbol \tau \to 0]{} f(\mathcal X) \oplus \cfrac{^{f(\mathcal X)} Df(\cal X)}{^\mathcal E D \cal X} {}^\mathcal E \boldsymbol \tau \tag{1.34.b} \label{1.34.b} \end{align*} $$

1.8 流形的不确定性与协方差传播 - Uncertainty in manifolds, covariance propagation

我们使用 right- $\oplus$ 和 $\ominus$ 定义切向量空间 $T\mathcal{_\bar X M}$ 中点 $\mathcal{\bar X} \in \mathcal M$ 周围的局部扰动 $\boldsymbol \tau$ 。

$$ \mathcal X = \bar{\mathcal X} \oplus \boldsymbol \tau, \qquad \boldsymbol \tau = \mathcal X \ominus \bar{\mathcal X} \ \ \in T\mathcal{_\bar X M} \tag{1.35} \label{1.35} $$

协方差矩阵可以通过标准期望算子 $\mathbb E[\cdot]$ 在 $\mathcal{\bar X}$ 处的切空间上正确定义，

$$ \boldsymbol\Sigma_\mathcal X \triangleq \mathbb E[\boldsymbol \tau \boldsymbol \tau^\top] = \mathbb E[(\mathcal X \ominus \bar{\mathcal X})(\mathcal X \ominus \bar{\mathcal X})^\top] \in \mathbb R^{m\times m} \tag{1.36}\label{1.36} $$

这样我们就可以在流形 $\mathcal X \sim \mathcal N(\bar{\mathcal X}, \boldsymbol\Sigma_\mathcal X)$ 上定义高斯变量，见 Fig. 10 。请注意，虽然我们写为 $\boldsymbol\Sigma_\mathcal X$ ，但协方差实际上是切线扰动 $\boldsymbol \tau$ 的协方差。由于 $\cal TM$ 的维度 $m$ 与 $\cal M$ 的自由度相匹配，因此这些协方差得到了明确定义（如果 ${\rm size}(\mathcal X) > \dim(\mathcal M)$ ，那么天真的定义 $\boldsymbol\Sigma_\mathcal X\mathbb = E[(\mathcal X \ominus \bar{\mathcal X})(\mathcal X \ominus \bar{\mathcal X})^\top]$ 总是定义不明确的，这是大多数非平凡流形 ( non-trivial manifolds) 的情况）。

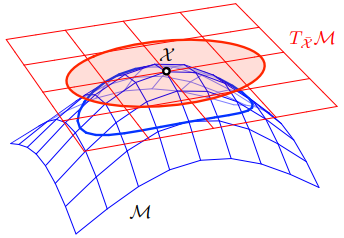
uncertainty

Fig. 10: 点 $\bar{\mathcal X} \in \mathcal N$ 周围的不确定性可以用点（红色）切线向量空间上的协方差来表示。利用 $\oplus$ $\eqref{1.35}$ 切线空间中的概率椭圆被包裹在流形（蓝色）上，从而反应了群上的概率集中区域。

扰动也可以在全局参考系中表示，即在原点 $T\mathcal{_E M}$ 的切线空间中，使用 left- $\oplus$ 和 $\ominus$

$$ \mathcal X = \boldsymbol \tau \oplus\bar{\mathcal X}, \qquad \boldsymbol \tau = \mathcal X \ominus \bar{\mathcal X} \ \ \in T\mathcal{_E M} \tag{1.37} \label{1.37} $$

这样就可以使用 $\eqref{1.36}$ 中的左减法在全局范围内指定协方差矩阵。例如，已知水平面内旋转的 3D 方向可以与协方差 $^\mathcal E \mathbf \Sigma = \mathrm{diag}(\sigma_\phi^2, \sigma_\theta^2, \infty)$ 相关联。由于 “水平” 是全局范畴，因此必须在全局参考中指定 $^\mathcal E \bf \Sigma$ 。

由于全局扰动和局部扰动是由伴随 $\eqref{1.18}$ 关联的，因此它们的协方差可以用以下公式进行转换

$$ ^\mathcal E \mathbf \Sigma _\mathcal X = \mathbf{Ad} \mathcal{ _X \ {}^X} \mathbf \Sigma _\mathcal X \ \mathbf{Ad} _\mathcal X {}^\top \tag{1.38} \label{1.38} $$

通过函数 $f : \mathcal M \to \mathcal N; \mathcal X \mapsto \mathcal Y = f (\mathcal X)$ 的协方差传播只需要使用雅可比矩阵 $\eqref{1.27.a}$ 进行线性化 $\eqref{1.29}$ 即可得到熟悉的公式

$$ \boldsymbol\Sigma_\mathcal Y \approx \cfrac{Df}{D\mathcal X} \boldsymbol\Sigma_\mathcal X \cfrac{Df}{D\mathcal X} ^\top \qquad \in \mathbb R^{n\times n} \tag{1.39} \label{1.39} $$

1.9 流形上的离散积分 - Discrete integration on manifolds

指数映射 $\mathcal X(t) = \mathcal X_0 \circ {\rm Exp}(\mathbf vt)$ 对流形上的恒定速度 $\mathbf v \in T_ {\mathcal X_0} \mathcal M$ 进行连续时间积分。非恒定速度 $\mathbf v(t)$ 通常通过将其分段为（短）持续时间 $\delta t_k$ 的分段恒定 $\mathcal v_k \in T _{\mathcal X _{k-1}} \cal M$ 并写入离散积分来处理

$$ \begin{align*} \mathcal X_k &= \mathcal X_0 \circ {\rm Exp}(\mathbf v_1 \delta t_1) \circ {\rm Exp}(\mathbf v_2 \delta t_2) \circ \cdots \circ {\rm Exp}(\mathbf v_k \delta t_k) \newline &=\mathcal X_0 \oplus \mathbf v_1 \delta t_1 \oplus \mathbf v_2 \delta t_2 \oplus \cdots \oplus \mathbf v_k \delta t_k \end{align*} $$

同样（Fig. 11），可以定义 $\boldsymbol \tau_k = \mathbf v_k \delta t_k$ ，并将积分构造为（小）离散切线步长 $\boldsymbol \tau_k \in T _{\mathcal X _{k-1}} \cal M$ 的 “总和”，即 $\mathcal X_k \triangleq \mathcal X_0 \oplus \boldsymbol \tau_1 \oplus \boldsymbol \tau_2 \oplus \cdots \oplus \boldsymbol \tau_k$ 。以递归形式写出所有这些变式，

$$ \mathcal X_k = \mathcal X_{k-1} \oplus \boldsymbol \tau_k = \mathcal X_{k-1} \circ {\rm Exp}(\boldsymbol \tau_k) = \mathcal X_{k-1} \circ {\rm Exp}(\mathbf v_k \delta t_k) \tag{1.40} \label{1.40} $$

常见的例子是将 3D 角速率 $\boldsymbol \omega$ 积分到旋转矩阵 $\mathbf R_k = \mathbf R_{k-1} {\rm Exp} (\boldsymbol\omega_k \delta t)$ ，或积分到四元数 $\mathbf q_k = \mathbf q_{k-1} {\rm Exp} (\boldsymbol\omega_k \delta t)$ 。

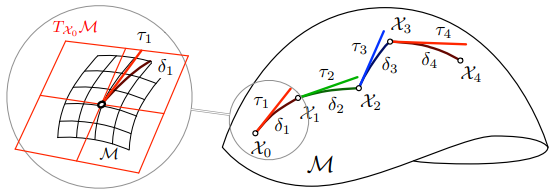
motion_integration

Fig. 11: 流形上的运动积分。每个运动数据都会产生一个步长 $\boldsymbol \tau_k \in T _{\mathcal X _{k-1}} \cal M$ ，该步长被包装成局部运动增量或 ‘delta’ $\delta_k = {\rm Exp}(\boldsymbol \tau_k) \in \cal M$ ，然后与 $\mathcal{X _{k-1}}$ 组成以产生 $\mathcal X_k = \mathcal X _{k-1} \circ \delta_k = \mathcal X _{k-1} \circ {\rm Exp}(\boldsymbol \tau_k) = \mathcal X _{k-1} \oplus \boldsymbol \tau_k \in \cal M$ 。

2. 流形上的微分规则 - DIFFERENTIATION RULES ON MANIFOLDS

对于我们使用的所有典型流形 $\cal M$，我们可以确定基本雅可比的反演、复合、指数化和作用 (inversion, composition, exponentiation and action) 的封闭形式 ( closed forms) 。此外，其中一些形式可以与伴随 ${\bf Ad} _\cal X$ 相关联，而 ${\bf Ad} _\cal X$ 是微分过程的核心部分。$\rm Log$、$\oplus$ 和 $\ominus$ 的其他形式可以很容易地从中推导出来。一旦找到这些形式或 “块”，所有其他的雅可比行都将遵循链式法则。除了所谓的左雅可比之外（我们将在下文中介绍），这里所建立的所有雅可比都是右雅可比，即由 $\eqref{1.27.a}$ 所定义。根据这里的提示，有兴趣的读者应该不会觉得建立左雅可比特别困难。对于不愿意这样做的读者，可以利用方程 $\eqref{1.32}$ 来实现这一目的，因为

$$ \cfrac{^\mathcal E Df(\cal X)}{D \cal X} = \mathbf{Ad} _{f(\mathcal X)} \cfrac{^\mathcal X Df(\cal X)}{D \cal X} \mathbf{Ad} _\mathcal X {}^{-1} \tag{2.1} \label{2.1} $$

使用符号 $\mathbf J_\mathcal X ^{f(\mathcal X)} \triangleq \frac{D f(\mathcal X)}{D \cal X}$ 和 $\mathbf J_\mathcal X ^\mathcal Y \triangleq \frac{D \mathcal Y}{D \cal X}$ ，还注意到 ${\bf Ad} _\cal X {}^{-1}$ 可以用 ${\bf Ad} _ {\mathcal X ^{-1}}$ 来实现 – 见 $\eqref{1.20.b}, \eqref{1.20.c}$ 及其下面的注释。

2.1 链式法则 - The chain rule

对于 $\mathcal Y = f(\mathcal X)$ 和 $\mathcal Z = g(\mathcal Y)$ ，有 $\mathcal Z = g(f(\mathcal X))$ ，则连锁法则有， $$ \frac{D \mathcal Z}{D \mathcal X} = \frac{D\mathcal Z}{D \mathcal Y} \frac{D \mathcal Y}{D \mathcal X} \qquad \text{or} \qquad \mathbf J_\mathcal X ^\mathcal Z = \mathbf J_\mathcal Y ^\mathcal Z \mathbf J_\mathcal X ^\mathcal Y \tag{2.2} \label{2.2} $$ 在此，右雅可比使用 $\eqref{1.29}$ 三次即可证明， $$ \begin{align*} g(f(\mathcal X)) \oplus \mathbf J_\mathcal X ^\mathcal Z \boldsymbol\tau \gets g(f(\mathcal X \oplus \boldsymbol\tau)) &\to g(f(\mathcal X) \oplus \mathbf J_\mathcal X ^\mathcal Y \boldsymbol\tau) \newline &\to g(f(\mathcal X)) \oplus \mathbf J_\mathcal Y ^\mathcal Z \mathbf J_\mathcal X ^\mathcal Y \boldsymbol\tau \end{align*} $$ 当 $\boldsymbol\tau \to 0$ 时（箭头表示极限），有 $\mathbf J_\mathcal X ^\mathcal Z = \mathbf J_\mathcal Y ^\mathcal Z \mathbf J_\mathcal X ^\mathcal Y$ 。左雅可比和交叉雅可比的证明类似，分别使用 $\eqref{1.31} \eqref{1.34.a} \eqref{1.34.b}$ 。请注意，当混合右、左和交叉雅可比行列式时，我们还需要链接参考系，例如 $$ \begin{alignat*}{2} \frac{^\mathcal Z D \mathcal Z }{^\mathcal E D \mathcal X} &= \frac{^\mathcal Z D \mathcal Z}{^\mathcal Y D \mathcal Y} \frac{^\mathcal Y D \mathcal Y}{^\mathcal E D \mathcal X} &&= \frac{^\mathcal Z D \mathcal Z}{^\mathcal E D \mathcal Y} \frac{^\mathcal E D \mathcal Y}{^\mathcal E D \mathcal X} \tag{2.3.a} \label{2.3.a} \newline \frac{^\mathcal E D \mathcal Z }{^\mathcal X D \mathcal X} &= \frac{^\mathcal E D \mathcal Z}{^\mathcal Y D \mathcal Y} \frac{^\mathcal Y D \mathcal Y}{^\mathcal X D \mathcal X} &&= \frac{^\mathcal E D \mathcal Z}{^\mathcal E D \mathcal Y} \frac{^\mathcal E D \mathcal Y}{^\mathcal X D \mathcal X} \tag{2.3.b} \label{2.3.b} \end{alignat*} $$ 其中，$\eqref{2.3.a}$ 的第一个特征通过证明如下， $$ \begin{align*} g(f(\mathcal X)) \oplus \frac{^\mathcal Z D \mathcal Z}{^\mathcal E D \mathcal X} {}^\mathcal E \boldsymbol\tau \xleftarrow[^\mathcal E \boldsymbol\tau \to 0]{\eqref{1.34.b}} g(f(^\mathcal E \boldsymbol\tau \oplus \mathcal X)) &\xrightarrow[^\mathcal E \boldsymbol\tau \to 0]{\eqref{1.34.b}} g \bigg( f(\mathcal X) \oplus \frac{^\mathcal Y D \mathcal Y}{^\mathcal E D \mathcal X} {}^\mathcal E \boldsymbol\tau \bigg) \to \newline &\xrightarrow[^\mathcal E \boldsymbol\tau \to 0]{\eqref{1.29}} g(f(\mathcal X)) \oplus \frac{^\mathcal Z D \mathcal Z}{^\mathcal Y D \mathcal Y} \frac{^\mathcal Y D \mathcal Y}{^\mathcal E D \mathcal X} {}^\mathcal E \boldsymbol\tau \end{align*} $$

2.2 基本雅可比块 - Elementary Jacobian blocks

2.2.1 逆 - Inverse

用 $\eqref{1.27.a}$ 定义， $$ \mathbf J_\mathcal X ^{{\mathcal X} ^{-1}} \triangleq \frac{^\mathcal X D \mathcal X^{-1}}{D \mathcal X} \qquad \in \mathbb R^{m \times n} \tag{2.4} \label{2.4} $$ 这可以通过使用 $\eqref{1.12.d} \eqref{1.19}$ 的伴随来确定，

$$ \begin{align*} \mathbf J_\mathcal X ^{{\mathcal X} ^{-1}} &= \lim _{\boldsymbol\tau \to 0} \frac{{\rm Log}((\mathcal X^{-1})^{-1} (\mathcal X \ {\rm Exp}(\boldsymbol\tau))^{-1} )}{\boldsymbol\tau} \newline &= \lim _{\boldsymbol\tau \to 0} \frac{{\rm Log}(\mathcal X \ {\rm Exp}(-\boldsymbol\tau) \mathcal X^{-1})}{\boldsymbol\tau} \newline &= \lim _{\boldsymbol\tau \to 0} \frac{(\mathcal X (-\boldsymbol\tau)^\wedge \mathcal X^{-1})^\vee}{\boldsymbol\tau} = - {\bf Ad} _\mathcal X \end{align*} \tag{2.5} \label{2.5} $$

2.2.2 复合 - Composition

用 $\eqref{1.27.a}$ 定义， $$ \begin{align*} \mathbf J_\mathcal X ^{\cal X \circ Y} &\triangleq \frac{^\mathcal X D \mathcal X \circ \mathcal Y}{D \mathcal X} & \in \mathbb R^{m \times n} \tag{2.6.a} \label{2.6.a} \newline \mathbf J_\mathcal Y ^{\cal X \circ Y} &\triangleq \frac{^\mathcal Y D \mathcal X \circ \mathcal Y}{D \mathcal Y} & \in \mathbb R^{m \times n} \tag{2.6.b} \label{2.6.b} \end{align*} $$ 通过使用 $\eqref{1.12.d} \eqref{1.19} \eqref{1.20.b}$ 来求解

$$ \begin{align*} \mathbf J _\mathcal X ^{\cal X \circ Y} &= \lim _{\boldsymbol\tau \to 0} \frac{{\rm Log}(({\cal XY})^{-1} (\mathcal X \ {\rm Exp}(\boldsymbol\tau) \mathcal Y))}{\boldsymbol\tau} \newline &= \lim _{\boldsymbol\tau \to 0} \frac{{\rm Log}(\mathcal Y^{-1} {\rm Exp}(\boldsymbol\tau) \mathcal Y)}{\boldsymbol\tau} \newline &= \lim _{\boldsymbol\tau \to 0} \frac{(\mathcal Y^{-1} \boldsymbol\tau^\wedge \mathcal Y)^\vee}{\boldsymbol\tau} = {\bf Ad} _\mathcal Y^{-1} \tag{2.7.a} \label{2.7.a} \newline \mathbf J _\mathcal Y ^{\cal X \circ Y} &= \cdots = \bf I \tag{2.7.b} \label{2.7.b} \end{align*} $$

2.2.3 $\mathcal M$ 的雅可比 - Jacobians of $\mathcal M$

我们将 $\mathcal M$ 的右雅可比定义为 $\mathcal X = {\rm Exp}(\boldsymbol\tau)$ 的右雅可比，即 $\boldsymbol\tau \in \mathbb R^m$ 的右雅可比， $$ \mathbf J_r (\boldsymbol\tau) \triangleq \frac{^\boldsymbol\tau D \ {\rm Exp}(\boldsymbol\tau)}{D \boldsymbol\tau} \in \mathbb R^{m \times n} \tag{2.8} \label{2.8} $$ 由 $\eqref{1.27.a}$ 定义。右雅可比将参数 $\boldsymbol \tau$ 的变化映射到 ${\rm Exp}(\boldsymbol \tau)$ 处局部切线空间的变化。从 $\eqref{1.27.a}$ 很容易证明，对于较小的 $\delta \boldsymbol\tau$ ，以下近似成立： $$ \begin{align*} {\rm Exp}(\boldsymbol\tau + \delta \boldsymbol\tau) &\approx {\rm Exp}(\boldsymbol\tau) {\rm Exp}(\mathbf J_r(\boldsymbol\tau) \delta \boldsymbol\tau) \tag{2.9.a} \label{2.9.a} \newline {\rm Exp}(\boldsymbol\tau) {\rm Exp}(\delta \boldsymbol\tau) &\approx {\rm Exp}(\boldsymbol\tau + \mathbf J_r^{-1}(\boldsymbol\tau) \delta \boldsymbol\tau) \tag{2.9.b} \label{2.9.b} \newline {\rm Log}( {\rm Exp}(\boldsymbol\tau) {\rm Exp}(\delta \boldsymbol\tau)) &\approx \boldsymbol\tau + \mathbf J_r^{-1}(\boldsymbol\tau) \delta \boldsymbol\tau \tag{2.9.c} \label{2.9.c} \end{align*} $$ 与之互补， $\mathcal M$ 的左雅可比定义为 $$ \mathbf J_l (\boldsymbol\tau) \triangleq \frac{^\mathcal E D \ {\rm Exp}(\boldsymbol\tau)}{D \boldsymbol\tau} \in \mathbb R^{m \times n} \tag{2.10} \label{2.10} $$ 利用左雅各布 $\eqref{1.30}$ ，得出近似值 $$ \begin{align*} {\rm Exp}(\boldsymbol\tau + \delta \boldsymbol\tau) &\approx {\rm Exp}(\mathbf J_l(\boldsymbol\tau) \delta \boldsymbol\tau) {\rm Exp}(\boldsymbol\tau) \tag{2.11.a} \label{2.11.a} \newline {\rm Exp}(\delta \boldsymbol\tau) {\rm Exp}(\boldsymbol\tau) &\approx {\rm Exp}(\boldsymbol\tau + \mathbf J_l^{-1}(\boldsymbol\tau) \delta \boldsymbol\tau) \tag{2.11.b} \label{2.11.b} \newline {\rm Log}({\rm Exp}(\delta \boldsymbol\tau) {\rm Exp}(\boldsymbol\tau)) &\approx \boldsymbol\tau + \mathbf J_l^{-1}(\boldsymbol\tau) \delta \boldsymbol\tau \tag{2.11.c} \label{2.11.c} \end{align*} $$ 左雅可比将参数 $\boldsymbol \tau$ 的变化映射为全局切线空间或李代数的变化。根据 $\eqref{2.9.a} \eqref{2.11.a}$ 可以将左雅可比和右雅可比与伴随式联系起来，

$$ {\bf Ad} _{{\rm Exp}(\boldsymbol\tau)} = \mathbf J_l(\boldsymbol\tau) \mathbf J_r^{-1}(\boldsymbol\tau) \tag{2.12} \label{2.12} $$

此外，链式法则允许我们将 $\mathbf J_r$ 和 $\mathbf J_l$ 联系起来

$$ \begin{align*} \mathbf J _r(-\boldsymbol \tau) &\triangleq \mathbf J _{-\boldsymbol \tau}^{{\rm Exp}(-\boldsymbol \tau)} = \mathbf J _\boldsymbol \tau ^{{\rm Exp}(-\boldsymbol \tau)} \mathbf J^\boldsymbol \tau _{-\boldsymbol \tau} = \mathbf J _\boldsymbol \tau ^{{\rm Exp}(\boldsymbol \tau)^{-1}} (- \mathbf I) \newline &= - \mathbf J^{{\rm Exp}(\boldsymbol \tau)^{-1}} _{{\rm Exp}(\boldsymbol \tau)} \mathbf J^{{\rm Exp}(\boldsymbol \tau)} _\boldsymbol \tau = {\bf Ad} _{{\rm Exp}(\boldsymbol \tau)} \mathbf J _r(\boldsymbol \tau) \newline &= \mathbf J _l(\boldsymbol \tau) \tag{2.13} \label{2.13} \end{align*} $$

对于常用的典型流形，存在 $\mathbf J_r, \mathbf J_r^{-1}, \mathbf J_l$ 和 $\mathbf J_l^{-1}$ 的闭合形式。请参阅附录以供参考。

2.2.4 群作用 - Group action

对于 $\cal X \in M$ 和 $v \in \cal V$ ，根据 $\eqref{1.27.a}$ 定义 $$ \begin{align*} \mathbf J_\mathcal X ^{\mathcal X \cdot v} &\triangleq \cfrac{^\mathcal X D \mathcal X \cdot v}{D \mathcal X} \tag{2.14.a} \label{2.14.a} \newline \mathbf J_v ^{\mathcal X \cdot v} &\triangleq \cfrac{^v D \mathcal X \cdot v}{D v} \tag{2.14.b} \label{2.14.b} \end{align*} $$ 由于群体作用取决于集合 $\cal V$，因此这些表达式无法通用。参考资料见附录。

2.3 有用可推导的雅可比块 - Useful, but deduced, Jacobian blocks

2.3.1 对数映射 - Log map

对于 $\boldsymbol\tau = {\rm Log}(\mathcal X)$ ，根据 $\eqref{2.9.c}$ 有， $$ \mathbf J_\mathcal X ^{{\rm Log}(\mathcal X)} = \mathbf J_r^{-1}(\boldsymbol \tau) \tag{2.15} \label{2.15} $$

2.3.2 加和减 - Plus and minus

有

$$ \begin{alignat*}{2} \mathbf J _\mathcal X ^{\mathcal X \oplus \boldsymbol\tau} &= \mathbf J _\mathcal X ^{\mathcal X \circ ({\rm Exp}(\boldsymbol\tau))} &&= {\bf Ad} _{{\rm Exp}(\boldsymbol\tau)} {}^{-1} \tag{2.16.a} \label{2.16.a} \newline \mathbf J _\boldsymbol\tau ^{\mathcal X \oplus \boldsymbol\tau} &= \mathbf J _{{\rm Exp}(\boldsymbol\tau)} ^{\mathcal X \circ ({\rm Exp}(\boldsymbol\tau))} \mathbf J _\boldsymbol\tau ^{{\rm Exp}(\boldsymbol\tau)} &&= \mathbf J _r(\boldsymbol\tau) \tag{2.16.b} \label{2.16.b} \end{alignat*} $$

设 $\mathcal Z = \mathcal X^{-1} \circ \mathcal Y$ 和 $\boldsymbol\tau = \mathcal Y \ominus \mathcal X = {\rm Log}(\mathcal Z)$ ，则

$$ \begin{alignat*}{2} \mathbf J _\mathcal X ^{\mathcal Y \ominus \mathcal X} &= \mathbf J _\mathcal Z ^{{\rm Log}(\mathcal Z)} \mathbf J _{\mathcal X^{-1}} ^\mathcal Z \mathbf J^{\mathcal X^{-1}} _\mathcal X &&= -\mathbf J_l^{-1}(\boldsymbol\tau) \tag{2.17.a} \label{2.17.a} \newline \mathbf J _\mathcal Y ^{\mathcal Y \ominus \mathcal X} &= \mathbf J _\mathcal Z ^{{\rm Log}(\mathcal Z)} \mathbf J _\mathcal Y ^\mathcal Z &&= \mathbf J_r^{-1}(\boldsymbol\tau) \tag{2.17.b} \label{2.17.b} \end{alignat*} $$

式 $\eqref{2.17.a}$ 证明如下

$$ \begin{align*} \mathbf J_\mathcal X ^{\mathcal Y \ominus \mathcal X} &= \mathbf J _{(\mathcal X^{-1} \circ \mathcal Y)} ^{{\rm Log}(\mathcal X^{-1} \circ \mathcal Y)} \mathbf J _{\mathcal X^{-1}} ^{(\mathcal X^{-1} \circ \mathcal Y)} \mathbf J^{\mathcal X^{-1}} _\mathcal X \newline \eqref{2.15}\eqref{2.7.a}\eqref{2.5} &= \ \ \ \mathbf J_r^{-1}(\boldsymbol\tau)\ {\bf Ad} _\mathcal Y {}^{-1} \ (-{\bf Ad} _\mathcal X) \newline \eqref{1.20.b}\eqref{1.20.c} &= - \mathbf J_r^{-1}(\boldsymbol\tau)\ {\bf Ad} _{\mathcal Y^{-1} \mathcal X} \newline &= -\mathbf J_r^{-1}(\boldsymbol\tau)\ {\bf Ad} _{{\rm Exp}(\boldsymbol\tau)}{}^{-1} \newline \eqref{2.12} &= -\mathbf J_l^{-1}(\boldsymbol\tau) \end{align*} $$

3. 复合流形 - COMPOSITE MANIFOLDS

我们可以把大的异质态看作流形复合体（或束 (bundles) ），这样做的代价是失去了与李理论的某些一致性，但好处是在符号和操作方面获得了一些优势。复合流形 $\mathcal M = \langle \mathcal M_1, \cdots, \mathcal M_M \rangle$ 不小于$M$ 个非交互流形的连接。这源于分别定义了作用于复合流形各块的同一性、逆和复合， $$ \mathcal E_\diamond \triangleq \begin{bmatrix} \mathcal E_1 \newline \vdots \newline \mathcal E_M \end{bmatrix} , \quad \mathcal X^\diamond \triangleq \begin{bmatrix} \mathcal X_1^{-1} \newline \vdots \newline \mathcal X_M^{-1} \end{bmatrix}, \quad \mathcal X \diamond \mathcal Y \triangleq \begin{bmatrix} \mathcal X_1 \circ \mathcal Y_1 \newline \vdots \newline \mathcal X_M \circ \mathcal Y_M \end{bmatrix} \tag{3.1} \label{3.1} $$

从而满足群公理，以及非交互回缩映射，为了统一符号，我们也将其标记为 “指数映射”（注意尖括号）， $$ {\rm Exp}\langle \boldsymbol\tau \rangle \triangleq \begin{bmatrix} {\rm Exp}(\boldsymbol\tau_1) \newline \vdots \newline {\rm Exp}(\boldsymbol\tau_M) \end{bmatrix} ,\quad {\rm Log}\langle \mathcal X \rangle \triangleq \begin{bmatrix} {\rm Log}(\mathcal X_1) \newline \vdots \newline {\rm Log}(\mathcal X_M) \end{bmatrix} \tag{3.2} \label{3.2} $$ 从而保证平滑性。这些产生了复合的右加和右减（注意矩形符号）， $$ \begin{align*} \mathcal X \boxplus \boldsymbol\tau &\triangleq \mathcal X \diamond {\rm Exp} \langle \boldsymbol\tau \rangle \tag{3.3.a} \label{3.3.a} \newline \mathcal Y \boxminus \mathcal X &\triangleq {\rm Log} \langle \mathcal X^\diamond \diamond \mathcal Y \rangle \tag{3.3.b} \label{3.3.b} \end{align*} $$ 这些考虑的关键结果（参见 Ex. 7）是可以使用 $\boxplus$ 和 $\boxminus$ 定义新的导数（我们在这里假设右导数，但这同样适用于左导数）， $$ \frac{Df(\mathcal X)}{D \mathcal X} \triangleq \lim _{\boldsymbol\tau \to 0} \frac{f(\mathcal X \boxplus \boldsymbol\tau) \boxminus f(\mathcal X)}{\boldsymbol\tau} \tag{3.4} \label{3.4} $$ 有了这个导数，作用于复合流形上的函数 $f : \mathcal M \to \mathcal N$ 的雅可比行列式可以在每个块的基础上确定，这产生简单的表达式，只需要了解复合流形的知识， $$ \frac{Df(\mathcal X)}{D \mathcal X} = \begin{bmatrix} \frac{D f_1}{D \mathcal X_1} & \cdots & \frac{D f_1}{D \mathcal X_M} \newline \vdots & \ddots & \vdots \newline \frac{D f_N}{D \mathcal X_1} & \cdots & \frac{D f_N}{D \mathcal X_M} \end{bmatrix} \tag{3.5} \label{3.5} $$

其中 $\cfrac{Df_i}{D \mathcal X_j}$ 均通过 $\eqref{1.27.a}$ 计算。对于较小的 $\boldsymbol\tau$ 值，以下成立 $$ f(\mathcal X \boxplus \boldsymbol\tau) \xrightarrow[\boldsymbol\tau \to 0]{} f(\mathcal X) \boxplus \cfrac{Df(\mathcal X)}{D \mathcal X} \boldsymbol\tau \quad \in \mathcal N \tag{3.6}\label{3.6} $$ 使用这些导数时，协方差和不确定性传播必须遵循约定。尤其，协方差矩阵 $\eqref{1.36}$ 变为 $$ \boldsymbol\Sigma_\mathcal X \triangleq \mathbb E [(\mathcal X \boxminus \bar{\mathcal X})(\mathcal X \boxminus \bar{\mathcal X})] \quad \in \mathbb R^{n\times n} \tag{3.7} \label{3.7} $$ 使用 $\eqref{3.4}$ 的线性化传播 $\eqref{1.39}$ 对其适用。

Example 7: $\mathbf{SE}(n)$ vs. $T(n) \times \mathbf{SO}(n)$ vs. $\langle \mathbb R^n, \mathbf{SO}(n) \rangle$
我们考虑位移空间 $\mathbf t \in \mathbb R^n$ 和旋转空间 $\mathbf R \in SO(n)$ 。为此，我们有了著名的刚性运动 $SE(n)$ 流形 $\mathbf M = \begin{bmatrix} \bf R & \bf t \newline \bf 0 & 1 \end{bmatrix}$ (见附录 C 和 D），也可以构造为 $T(n) \times \mathbf{SO}(n)$ （见附录 A、B 和 E）。这两者非常相似，但切线参数不同：$SE(n)$ 使用 $\boldsymbol\tau = (\boldsymbol\theta, \boldsymbol\rho), \mathbf M = \exp(\boldsymbol\tau^\wedge)$ ，而 $T(n) \times \mathbf{SO}(n)$ 使用 $\boldsymbol\tau = (\boldsymbol\theta, \mathbf p), \mathbf M = \exp(\mathbf p^\wedge)\exp(\boldsymbol\theta^\wedge)$ 。它们共享旋转部分 $\boldsymbol\theta$ ，但显然 $\boldsymbol\rho \neq \mathbf p$（详见 [¹⁰，第 35 页]）。简而言之，$\mathbf{SE}(n)$ 作为连续体同时执行平移和旋转，而 $T(n) \times \mathbf{SO}(n)$ 则执行链式平移 + 旋转。与此形成鲜明对比的是，在复合 $\langle \mathbb R^n, \mathbf{SO}(n) \rangle$ 中，旋转和平移完全没有相互作用。将合成与 $\mathrm{Exp}()$ 结合起来，我们就得到了（右）加算子 $$ \begin{align*} SE(n) &: \quad \mathbf M \oplus \boldsymbol\tau = \begin{bmatrix} \mathbf R \ \mathrm{Exp}(\boldsymbol\theta) & \mathbf t + \mathbf{RV}(\boldsymbol\theta) \boldsymbol\rho \newline \bf 0 & 1 \end{bmatrix} \newline T(n) \times SO(n) &: \quad \mathbf M \oplus \boldsymbol\tau = \begin{bmatrix} \mathbf R \ \mathrm{Exp}(\boldsymbol\theta) & \mathbf t + \mathbf{R} \mathbf p \newline \bf 0 & 1 \end{bmatrix} \newline \langle \mathbb R^n, SO(n) \rangle &: \quad \mathbf M \boxplus \boldsymbol\tau = \begin{bmatrix} \mathbf t + \mathbf p \newline \mathbf R \ \mathrm{Exp}(\boldsymbol\theta) \end{bmatrix} \end{align*} $$ 其中，$\oplus$ 可用于系统动力学，如运动积分，但通常不包括 $\boxplus$ ，后者可用于扰动建模。它们各自的减运算符为 $$ \begin{align*} SE(n) &: \quad \mathbf M_2 \ominus \mathbf M_1 = \begin{bmatrix} \mathbf V_1^{-1} \mathbf R_1^\top(\mathbf p_2 - \mathbf p_1) \newline \mathrm{Log}(\mathbf R^\top_1 \mathbf R_2) \end{bmatrix} \newline T(n) \times SO(n) &: \quad \mathbf M_2 \ominus \mathbf M_1 = \begin{bmatrix} \mathbf R_1^\top(\mathbf p_2 - \mathbf p_1) \newline \mathrm{Log}(\mathbf R^\top_1 \mathbf R_2) \end{bmatrix} \newline \langle \mathbb R^n, SO(n) \rangle &: \quad \mathbf M_2 \ominus \mathbf M_1 = \begin{bmatrix} \mathbf p_2 - \mathbf p_1 \newline \mathrm{Log}(\mathbf R^\top_1 \mathbf R_2) \end{bmatrix} \end{align*} $$ 有趣的是，$\boxminus$ 可用来评估误差和不确定性。这使得 $\boxplus$ 和 $\boxminus$ 成为计算导数和协方差的重要运算符。

4. 基于地标的定位与建图 - LANDMARK-BASED LOCALIZATION AND MAPPING

我们提供了机器人定位和建图理论的三个应用示例。第一个是用于基于地标的定位的卡尔曼滤波器。第二个是基于图的平滑方法，用于同时定位和建图。第三个增加了传感器自校准。它们基于一个共同的设置，解释如下。

考虑一个平面机器人（三维情况见第 V-D 节），其周围有少量准时地标或信标。机器人以轴向速度和角速度的形式接收控制动作，并能根据自己的参照系测量信标的位置。

机器人位姿位于 $SE(2)$（App.C）中，信标位置位于 $\mathbb R^2$（App.E）中， $$ \mathcal X = \begin{bmatrix} \bf R & \bf t \newline \bf 0 & 1 \end{bmatrix} \in SE(2) , \qquad \mathbf b_k = \begin{bmatrix} x_k \newline y_k \end{bmatrix} \in \mathbb R^2 \tag{4.1} \label{4.1} $$ 控制信号 $\bf u$ 是 $\mathfrak{se}(2)$ 中的扭曲，包括纵向速度 $v$ 和角速度 $\omega$ ，没有横向速度分量，在采样时间 $\delta t$上积分。控制受到加性高斯噪声 $\mathbf w \sim \mathcal N (\mathbf 0, \mathbf W)$ 的干扰。该噪声通过 $\sigma_s \neq 0$ 的值来考虑车轮可能出现的横向打滑

$$ \begin{align*} \mathbf u &= \begin{bmatrix} u_v \newline u_s \newline u_\omega \end{bmatrix} = \begin{bmatrix} v \ \delta t \newline 0 \newline \omega \ \delta t \end{bmatrix} + \mathbf w \qquad \in \mathfrak{se}(2) \tag{4.2.a} \label{4.2.a} \newline \mathbf W &= \begin{bmatrix} \sigma_v^2 \delta t & 0 & 0 \newline 0 & \sigma_s^2 \delta t & 0 \newline 0 & 0 & \sigma_\omega^2 \delta t \end{bmatrix} \qquad \in \mathbb R^{3\times3} \tag{4.2.b} \label{4.2.b} \end{align*} $$

当控制 $\mathbf u_j$ 在时间 $j$ 到达时，机器人姿态将根据 $\eqref{1.40}$ 进行更新， $$ \mathcal X_j = \mathcal X_i \oplus \mathbf u_j \triangleq \mathcal X_i {\rm Exp}(\mathbf u_j) \tag{4.3} \label{4.3} $$ 地标测量是测距和方位类型的测量，但为简单起见采用笛卡尔形式。其噪声 $\mathbf n \sim \mathcal N (\mathbf 0, \mathbf N)$ 为零均值高斯噪声， $$ \begin{alignat*}{2} \mathbf y_k &= \mathcal X^{-1} \cdot \mathbf b_k + \mathbf n = \mathbf R^\top (\mathbf b_k - \mathbf t) + \mathbf n \quad && \in \mathbb R^2 \tag{4.4.a} \label{4.4.a} \newline \mathbf N &= \begin{bmatrix} \sigma_x^2 & 0 \newline 0 & \sigma_y^2 \end{bmatrix} && \in \mathbb R^{2\times2} \tag{4.4.b} \label{4.4.b} \end{alignat*} $$ 其中我们注意到刚性运动运算 $\mathcal X^{-1} \cdot \mathbf b_k$（见附录 C）。

4.1 在流形上使用误差状态卡尔曼滤波器进行定位 - Localization with error-state Kalman filter on manifold

首先考虑位于已知位置的信标 $\mathbf b_k$ 。将需要估计的姿态定义为 $\hat{\cal X} \in SE(2)$ 。估计误差 $\delta\mathbf x$ 及其协方差 $\bf P$ 在 $\hat{\cal X}$ 的切线空间中表示为 $\eqref{1.35}\eqref{1.36}$

$$ \begin{align*} \delta\mathbf x &\triangleq \mathcal X \ominus \hat{\cal X} &&\in \mathbb R^3 \tag{4.5.a} \label{4.5.a} \newline \mathbf P &\triangleq \mathbb E[(\mathcal X \ominus \hat{\cal X})(\mathcal X \ominus \hat{\cal X})^\top] &&\in \mathbb R^{3\times3} \tag{4.5.b}\label{4.5.b} \end{align*} $$

每次机器人运动时，都会应用 ESKF 预测

$$ \begin{align*} \hat{\cal X}_j &= \hat{\cal X}_i \oplus \mathbf u_j \tag{4.6.a}\label{4.6.a} \newline \mathbf P_j &= \mathbf F \mathbf P_i \mathbf F^T + \mathbf G \mathbf W_j \mathbf G^\top \tag{4.6.b}\label{4.6.b} \end{align*} $$

雅可比行列式是根据附录 C 中的块计算出来的，

$$ \begin{alignat}{2} \mathbf F &\triangleq \mathbf J _{\mathcal X_i}^{\mathcal X_j} &= \mathbf J _{\hat{\cal X} _i}^{\hat{\cal X} _i \oplus \mathbf u_j} &= \mathbf{Ad} _{{\rm Exp}(\mathbf u_j)}{}^{-1} \tag{4.7.a}\label{4.7.a} \newline \mathbf G &\triangleq \mathbf J _{\mathbf u_j}^{\mathcal X_j} &= \mathbf J _{\mathbf u_j}^{\hat{\cal X} _i \oplus \mathbf u_j} &= \mathbf J_r(\mathbf u_j) \tag{4.7.b}\label{4.7.b} \end{alignat} $$

在每次信标测量 $\mathbf y_k$ 时，都要进行 ESKF 校正

$$ \begin{align*} {\rm Innovation} &: &\mathbf z &= \mathbf y_k - \hat{\cal X}^{-1} \cdot \mathbf b_k \tag{4.8.a}\label{4.8.a} \newline {\rm Innovation \ \ cov.} &: &\mathbf Z &= \mathbf{HPH}^\top + \mathbf N \tag{4.8.b}\label{4.8.b} \newline {\rm Kalman \ \ gain} &: &\mathbf K &= \mathbf{PH}^\top \mathbf Z^{-1} \tag{4.8.c}\label{4.8.c} \newline {\rm Observed \ \ error} &: &\delta\mathbf x & = \mathbf{Kz} \tag{4.8.d}\label{4.8.d} \newline {\rm State \ \ update} &: &\hat{\cal X} &\gets \hat{\cal X} \oplus \delta\mathbf x \tag{4.8.e}\label{4.8.e} \newline {\rm Cov. \ update} &: &\mathbf P &\gets \mathbf P - \mathbf{KZK}^\top \tag{4.8.f}\label{4.8.f} \end{align*} $$

雅可比行列式是根据附录 C 中的块计算出来的，

$$ \begin{align*} \mathbf H &\triangleq \mathbf J_ {\cal X}^{\mathcal X^{-1} \cdot \mathbf b_k} = \mathbf J_ {\mathcal X^{-1}}^{\mathcal X^{-1} \cdot \mathbf b_k} \mathbf J_ {\cal X}^{\mathcal X^{-1}} \newline &= \begin{bmatrix} \mathbf R^\top & \mathbf R^\top[1]_ \times \mathbf b_k \end{bmatrix} \begin{bmatrix} -\mathbf R & [1]_ \times \mathbf t \newline \mathbf 0 & -1 \end{bmatrix} \newline &= - \begin{bmatrix}\bf I & \mathbf R^\top [1]_\times (\mathbf b_k - \mathbf t) \end{bmatrix} \end{align*} $$

请注意，与标准 EKF 相比，唯一的变化是在 $\eqref{4.6.a}$ 和 $\eqref{4.8.e}$ 中，正则 $+$ 被 $\oplus$ 取代。相反，雅各比因子都是用李理论计算的（见附录 C）。有趣的是，它们的用法与标准 EKF 相同。例如，请参见卡尔曼增益方程，即标准的 $\mathbf K = \mathbf P \mathbf H^\top(\mathbf{HPH}^\top + \mathbf N)^{-1}$ 。

4.2 基于图形优化的平滑与建图 - Smooting and Mapping with graph-based optimization

现在考虑的是平滑与建图（SAM）问题，其中需要估计的变量是信标的位置和机器人的轨迹。我们选择的求解器是基于图的迭代最小二乘优化器。为简单起见，我们假设轨迹由三个机器人姿势 $\lbrace \mathcal X_1 \cdots \mathcal X_3 \rbrace$ 和一个包含三个信标 $\lbrace \mathbf b_4 \cdots \mathbf b_6 \rbrace$ 的世界组成。问题状态是

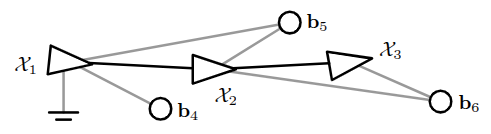
$$ \mathcal X = \langle \mathcal X_1, \mathcal X_2, \mathcal X_3, \mathbf b_4, \mathbf b_5, \mathbf b_6 \rangle, \quad \mathcal X_i \in SE(2), \quad \mathbf b_k \in \mathbb R^2 \tag{4.9}\label{4.9} $$ SAM factor graph

Fig. 12: 具有 3 个姿势和 3 个信标的 SAM 因子图。图中每个测量值都有一个因子。图中有 2 个运动因子（黑色）和 5 个信标因子（灰色）。$\mathcal X_1$ 上的先验因子提供了全局可观测性。

由此得出的因子图 ¹¹ 如 Fig.12 所示。图中每个先验值或测量值都有一个因子。从姿态 $i$ 到 $j$ 的运动测量值来自 $\eqref{4.3}$，而从姿态 $i$ 到信标 $k$ 的测量值则来自 $\eqref{4.4.a}$ ,

$$ \begin{align*} \mathbf u_{ij} &= \mathcal X_j \ominus \mathcal X_i + \mathbf w_{ij} = {\rm Log}(\mathcal X_i^{-1}\mathcal X_j) + \mathbf w_{ij} \tag{4.10.a} \label{4.10.a} \newline \mathbf y_{ik} &= \mathcal X_i^{-1} \cdot \mathbf b_k + \mathbf n_{ik} \tag{4.10.b} \label{4.10.b} \end{align*} $$

每个因子都有一个信息矩阵，$\mathbf \Omega_1 \triangleq \mathbf W_1^{-1}$ ，$\mathbf \Omega_{ij} \triangleq \mathbf W_{ij}^{-1}$ 和 $\mathbf \Omega_{ik} \triangleq \mathbf N_{ik}^{-1}$ 。期望残差为，

$$ \begin{align*} \text{prior residual} &:& \mathbf r_1(\mathcal X) &= \mathbf\Omega_1^{\top/2} (\mathcal X_1 \ominus \hat{\cal X} _1) \newline \text{motion residual} &:& \mathbf r _{ij}(\mathcal X) &= \mathbf\Omega _{ij}^{\top/2} (\mathbf u _{ij} - (\hat{\mathcal X} _j \ominus \hat{\cal X} _i) \newline \text{beacon residual} &:& \mathbf r _{ik}(\mathcal X) &= \mathbf\Omega _{ik}^{\top/2} (\mathbf y _{ik} - \hat{\cal X} _i^{-1} \cdot \hat{\bf b} _k) \end{align*} $$

最佳更新步骤 $\delta \bf x$ 源自最小化

$$ \delta\mathbf x^* = \underset{\delta\mathbf x}{\arg\min} \sum_{p \in \mathcal P} \mathbf r_p(\mathcal X \boxplus \delta\mathbf x)^\top \mathbf r_p (\mathcal X \boxplus \delta\mathbf x) \tag{4.11}\label{4.11} $$

其中 $\mathcal P = \lbrace 1, 12, 23, 14, 15, 25, 26, 36 \rbrace$ 为每次测量的节点对集合（见 Fig.12 ）。问题的迭代解决方法如下。根据 $\eqref{3.6}$ ，将总和 $\eqref{4.11}$ 中的每个残差线性化为 $\mathbf r_p (\mathcal X \boxplus \delta \mathbf x) \approx \mathbf r_p (\mathcal X) \boxplus \mathbf J_{\cal X}^{\mathbf r_p} \delta \mathbf x$ ，其中 $\mathbf J_{\cal X}^{\mathbf r_p}$ 为稀疏雅各布。这些雅各布矩阵的非零块，即 $\mathbf J_{\mathcal X_1}^{\mathbf r_1}, \mathbf J_{\mathcal X_i}^{\mathbf r_{ij}}, \mathbf J_{\mathcal X_j}^{\mathbf r_{ij}}, \mathbf J_{\mathcal X_i}^{\mathbf r_{ik}}$ 和 $\mathbf J_{\mathbf b_k}^{\mathbf r_{ik}}$ ，可以按照第 4.1 节中的方法轻松计算，并注意到根据定义 $\mathbf J_ {\delta\mathbf x}^{f(\mathcal X \oplus \delta\mathbf x)}|_ {\delta \mathbf x = 0} = \mathbf J_ {\cal X}^{f(\mathcal X \oplus \delta \mathbf x)}|_ {\delta \mathbf x = 0} = \mathbf J_ {\cal X}^{f(\mathcal X)}$ 。建立总雅可比矩阵和残差向量

$$ \mathbf J = \begin{bmatrix} \mathbf J_{\mathcal X_1}^{\mathbf r_1} & 0 & 0 & 0 & 0 & 0 \newline \mathbf J_{\mathcal X_1}^{\mathbf r_{12}} & \mathbf J_{\mathcal X_2}^{\mathbf r_{12}} & 0 & 0 & 0 & 0 \newline 0 & \mathbf J_{\mathcal X_2}^{\mathbf r_{23}} & \mathbf J_{\mathcal X_3}^{\mathbf r_{23}} & 0 & 0 & 0 \newline \mathbf J_{\mathcal X_1}^{\mathbf r_{14}} & 0 & 0 & \mathbf J_{\mathbf b_4}^{\mathbf r_{14}} & 0 & 0 \newline \mathbf J_{\mathcal X_1}^{\mathbf r_{15}} & 0 & 0 & 0 & \mathbf J_{\mathbf b_5}^{\mathbf r_{15}} & 0 \newline 0 & \mathbf J_{\mathcal X_2}^{\mathbf r_{25}} & 0 & 0 & \mathbf J_{\mathbf b_5}^{\mathbf r_{25}} & 0 \newline 0 & \mathbf J_{\mathcal X_2}^{\mathbf r_{26}} & 0 & 0 & 0 & \mathbf J_{\mathbf b_6}^{\mathbf r_{26}} \newline 0 & 0 & \mathbf J_{\mathcal X_3}^{\mathbf r_{36}} & 0 & 0 & \mathbf J_{\mathbf b_6}^{\mathbf r_{36}}
\end{bmatrix} \quad \mathbf r = \begin{bmatrix} \mathbf r_1 \newline \mathbf r_{12} \newline \mathbf r_{23} \newline \mathbf r_{14} \newline \mathbf r_{15} \newline \mathbf r_{25} \newline \mathbf r_{26} \newline \mathbf r_{36} \end{bmatrix} \tag{4.12} \label{4.12} $$

现在将线性化的 $\eqref{4.11}$ 转化为 ¹² 最小化

$$ \delta \mathbf x^* = \underset{\delta\mathbf x}{\arg \min} \lVert \mathbf r + \mathbf J \delta \mathbf x \rVert^2 \tag{4.13} \label{4.13} $$ 利用 $\bf J$ 的伪逆，通过最小二乘法求解（对于大型问题，需要 QR ¹², ¹¹ 或 Cholesky ¹³, ¹⁴ 因式分解），

$$ \delta \mathbf x^* = - (\mathbf J^\top \mathbf J)^{-1} \mathbf J^\top \mathbf r \tag{4.14} \label{4.14} $$ 得出用于更新状态的最优步长 $\delta\bf x$ ，

$$ \mathcal X \gets \mathcal X \boxplus \delta\mathbf x^* \tag{4.15}\label{4.15} $$ 该过程反复进行，直至收敛。在此强调 $\eqref{4.9}$ 中复合符号的使用，它允许分块定义雅各布因子 $\eqref{4.12}$ 和更新 $\eqref{4.15}$ 。我们还注意到在运动和测量模型中使用了 $SE(2)$ 流形，正如我们在第 4.1 节 ESKF 案例中所做的那样。

4.3 带有自标定的平滑与建图 - Smoothing and mapping with self-calibration

这小节考虑的问题与上述问题相同，但运动传感器受到未知校准偏差 $\mathbf c = (c_v, c_w)^\top$ 的影响，因此，现在的控制是 $\tilde{\mathbf u} = (v\delta t + c_v, 0, \omega\delta t + c_w)^\top + \mathbf w$ 。我们定义了偏差修正函数 $c()$ ， $$ \mathbf u = c(\tilde{\bf u}, \mathbf c) \triangleq \begin{bmatrix} \tilde u_v - c_v \newline \tilde u_s \newline \tilde u_w - c_w \end{bmatrix} \in \mathbb R^3 \cong \mathfrak{se}(2) \tag{4.16}\label{4.16} $$ 状态复合体中增加了未知数 $\bf c$ ， $$ \mathcal X = \langle \mathbf c, \mathcal X_1, \mathcal X_2, \mathcal X_3, \mathbf b_4, \mathbf b_5, \mathbf b_6 \rangle, \quad \mathbf c \in \mathbb R^2, \quad \mathcal X_i \in SE(2), \quad \mathbf b_k \in \mathbb R^2 $$ 运动残差变为导数公式和协方差处理公式与标准向量空间中的相应公式极为相似。

第四，我们特别强调雅各布矩阵的定义、几何解释和计算。为此，我们引入了雅各布矩阵和协方差的符号，使操作变得直观有力。特别是，通过这种符号，链式法则清晰可见。这有助于建立直觉和减少错误。

第五，我们在后面的附录中介绍了机器人学中最常见的群的大量公式。在二维中，我们介绍了单位复数沙旋转矩阵 SO(2) 的旋转群，以及刚性运动群 SE(2)。在三维空间中，我们介绍了用于旋转的单位四元数沙盘旋转矩阵 SO(3) 群，以及刚性运动群 SE(3)。我们还介绍了任意维度的平移群，它们可以通过标准向量空间 Runder 加法或矩阵平移群 T (n) 乘法来实现。

第六，我们介绍了一些应用实例，以说明李理论能够优雅而精确地解决机器人问题。复合群这一略显幼稚的概念有助于将异质状态向量统一为一种李理论形式。

最后，我们为本文附带了实现本文所述工具的新 C++ 库 manif [7]。manif 的网址是 https://github.com/artivis/manif。第五节中的应用将以 manif 为例进行演示。

虽然我们没有引入任何新的理论材料，但我们相信，这里所揭示的谎言理论的形式将有助于许多研究人员进入这一领域，为他们未来的发展提供帮助。我们也相信，这本身就是一个有价值的贡献。

$$ \mathbf r _{ij}(\mathcal X) = \mathbf\Omega _{ij}^{\top/2} (c(\tilde{\mathbf u} _{ij}, \mathbf c) - (\hat{\mathcal X} _j \ominus \hat{\cal X} _i) $$

操作步骤与上文第 4.2 节相同，只是对总雅各布矩阵进行了修改，在左侧增加了一列，

$$ \mathbf J = \begin{bmatrix} 0 & \mathbf J_{\mathcal X_1}^{\mathbf r_1} & 0 & 0 & 0 & 0 & 0 \newline \mathbf J_{\bf c}^{\mathbf r_{12}} & \mathbf J_{\mathcal X_1}^{\mathbf r_{12}} & \mathbf J_{\mathcal X_2}^{\mathbf r_{12}} & 0 & 0 & 0 & 0 \newline \mathbf J_{\bf c}^{\mathbf r_{23}} & 0 & \mathbf J_{\mathcal X_2}^{\mathbf r_{23}} & \mathbf J_{\mathcal X_3}^{\mathbf r_{23}} & 0 & 0 & 0 \newline 0 & \mathbf J_{\mathcal X_1}^{\mathbf r_{14}} & 0 & 0 & \mathbf J_{\mathbf b_4}^{\mathbf r_{14}} & 0 & 0 \newline 0 & \mathbf J_{\mathcal X_1}^{\mathbf r_{15}} & 0 & 0 & 0 & \mathbf J_{\mathbf b_5}^{\mathbf r_{15}} & 0 \newline 0 & 0 & \mathbf J_{\mathcal X_2}^{\mathbf r_{25}} & 0 & 0 & \mathbf J_{\mathbf b_5}^{\mathbf r_{25}} & 0 \newline 0 & 0 & \mathbf J_{\mathcal X_2}^{\mathbf r_{26}} & 0 & 0 & 0 & \mathbf J_{\mathbf b_6}^{\mathbf r_{26}} \newline 0 & 0 & 0 & \mathbf J_{\mathcal X_3}^{\mathbf r_{36}} & 0 & 0 & \mathbf J_{\mathbf b_6}^{\mathbf r_{36}}
\end{bmatrix} $$

其中 $\mathbf J_{\bf c}^{\mathbf r_{ij}} = \Omega_{ij}^{\top/2} \mathbf J_{\bf c}^{c(\mathbf u_{ij}, \mathbf c)}$ ，$\mathbf J_{\bf c}^{c(\mathbf u_{ij}, \mathbf c)}$ 为 $\eqref{4.16}$ 的 $3\times2$ 雅各比。通过 $\eqref{4.14}\eqref{4.15}$ 可以得到最优解。由此得到的最优状态 $\cal X$ 包括对 $\bf c$ 的最优估计，即传感器偏差的自我校准。

4.4 3D 实现 - 3D implementations

要将上述所有示例转化为三维模型，其实非常容易。只需在正确的空间中定义所有变量即可：$\mathcal X \in SE(3)$ 和 $\mathbf u \in \mathbb R^6 = \mathfrak{se}(3)$ （附录 D），以及 $\lbrace \mathbf b_k, \mathbf y \rbrace \in \mathbb R^3$（附录 E）。雅各比矩阵和协方差矩阵将以适当的大小出现。这里的兴趣在于认识到算法中的所有数学，即从 $\eqref{4.5.a}$ 开始，对于二维和三维是完全一样的。

5. 总结 - CONCLUSION

该论文对需熟练掌握状态估计的读者来说，以一种有用形式介绍了李理论的基本内容，重点是机器人应用范畴。为此，采取了多项措施：

首先，选材尽量避免抽象的数学概念。这有助于突出李理论的重点，使其工具更容易理解和使用。
其次，选择了一种教学方法，其中有大量冗余。正文是通俗的，涵盖了李理论的抽象要点。同时还附有方框示例，将抽象概念与特定的李群联系起来，并提供了大量附有详细说明的图表。
第三，提倡使用方便的运算符，如大写的 $\text{Exp}()$ 和 $\text{Log}()$ 映射，以及加号和减号运算符 $\oplus,\ominus, \boxplus,\boxminus$ 。通过这些运算符，我们可以对切线空间的笛卡尔表示法进行运算，生成导数公式和协方差处理公式与标准向量空间中的相应公式极为相似。
第四，特别强调雅各比矩阵的定义、几何解释和计算。为此，引入了雅各比矩阵和协方差的符号，使操作变得直观有力。特别是，通过这种符号，链式法则清晰可见。这有助于建立直觉和减少错误。
第五，在后面的附录中介绍了机器人学中最常见的群的大量公式。在二维中，我们介绍了单位复数 $S^1$ 的旋转群和旋转矩阵 $SO(2)$ ，以及刚体运动群 $SE(2)$ 。在三维空间中，我们介绍了用于旋转的单位四元数 $S^3$ 的旋转矩阵 $SO(3)$ 群，以及刚性运动群 $SE(3)$ 。我们还介绍了任意维度的平移群，它们可以通过加法运算下的标准向量空间 $\mathbb R^n$ 或乘法运算下的矩阵平移群 $T(n)$ 来实现。
第六，介绍了一些应用实例，以说明李理论能够优雅而精确地解决机器人问题。复合群这一略显幼稚的概念有助于将异质状态向量统一为一种李理论形式。
最后，本文附带了实现本文所述工具的新 C++ 库 manif 。

虽然我们没有引入任何新的理论材料，但我们相信，这里所揭示的李理论的形式将有助于许多研究人员进入这一领域，为他们未来的发展提供帮助。我们也相信，这本身就是一个有价值的贡献。

附录 A: 2D 旋转群 $S^1$ 和 $SO(2)$ - APPENDIX A: THE 2D ROTATION GROUPS $S^1$ AND $SO(2)$

李群 $S^1$ 是复数乘积下的单位复数群。它的拓扑结构是单位圆或单位球 (1-sphere)，因此得名 $S^1$。该群、李代数和向量元素的形式为 $$ \mathbf z = \cos\theta + i\sin\theta, \quad \tau^\wedge = i\theta, \quad \tau = \theta \tag{A.1}\label{A.1} $$ 通过共轭 $\mathbf z^{-1} = \mathbf z^∗$ 和乘积 $\mathbf z_a \circ \mathbf z_b = \mathbf z_a \mathbf z_b$ 可以实现逆和复合。 $SO(2)$ 群是矩阵乘法下平面内特殊正交矩阵或旋转矩阵的群。群、李代数和向量元素的形式为 $$ \mathbf R = \begin{bmatrix} \cos\theta & -\sin\theta \newline \sin\theta & \cos\theta \end{bmatrix}, \quad \tau^\wedge = [\theta]_\times \triangleq \begin{bmatrix} 0 & -\theta \newline \theta & 0 \end{bmatrix}, \quad \tau = \theta \tag{A.2}\label{A.2} $$ 通过转置 $\mathbf R^{-1} = \mathbf R^\top$ 和乘积 $\mathbf R_a \circ \mathbf R_b = \mathbf R_a \mathbf R_b$ 可以实现逆和复合。这两个群都旋转 2 维向量，它们的切空间同构。因此，我们将它们放在一起研究。

A.a 指数和对数映射 - Exp and Log maps

对于 $S^1$ 的复数和 $SO(2)$ 的旋转矩阵，可以定义 $\rm Exp$ 和 $\rm Log$ 映射。对于 $S^1$ ，我们有 $$ \begin{alignat*}{3} \mathbf z &= \text{Exp}(\theta) &&= \cos\theta + i \sin\theta &\qquad& \in \mathbb C \tag{A.3.a} \label{A.3.a} \newline \theta &= \text{Log}(\mathbf z) &&= \arctan(\rm{Im}(\mathbf z), \rm{Re}(\mathbf z)) && \in \mathbb R \tag{A.3.b} \label{A.3.b} \end{alignat*} $$ 其中 $\eqref{A.3.a}$ 是欧拉公式，而对于 $SO(2)$ ， $$ \begin{alignat*}{2} \mathbf R &= \text{Exp}(\theta) &&= \begin{bmatrix} \cos\theta & -\sin\theta \newline \sin\theta & \cos\theta \end{bmatrix} &\quad& \in \mathbb R^{2\times2} \tag{A.4.a}\label{A.4.a} \newline \theta &= \text{Log}(\mathbf R) &&= \arctan(r_{21}, r_{11}) && \in \mathbb R \tag{A.4.b} \label{A.4.b} \end{alignat*} $$

A.b 逆、复合、幂映射 - Inverse, composition, exponential map

考虑一般的二维旋转元素，并用无衬线字体 (sans-serif font) $\sf Q,R$ 表示，有 $$ \begin{align*} \mathsf R(\theta)^{-1} &= \mathsf R(-\theta) \tag{A.5.a}\label{A.5.a} \newline \mathsf Q \circ \mathsf R &= \mathsf R \circ \mathsf Q \tag{A.5.b}\label{A.5.b} \end{align*} $$ 即，平面旋转是可交换的。遵循 $$ \begin{align*} \text{Exp}(\theta_1 + \theta_2) &= \text{Exp}(\theta_1) \circ \text{Exp}(\theta_2) \tag{A.6.a} \label{A.6.a} \newline \text{Log}(\mathsf Q \circ \mathsf R) &= \text{Log}(\mathsf Q) + \text{Log}(\mathsf R) \tag{A.6.b} \label{A.6.b} \newline \mathsf Q \ominus \mathsf R &= \theta_Q - \theta_R \tag{A.6.c} \label{A.6.c} \newline \end{align*} $$

A.c 雅可比块 - Jacobian blocks

由于我们定义的导数映射了切向量空间，而这些空间对于 $S^1$ 和 $SO(2)$ 的平面旋转流形来说是重合的，即 $\theta = \rm{Log}(\mathbf z) = \rm{Log}(\mathbf R)$，因此雅各比值与所使用的表示（$\bf z$ 或 $\bf R$）无关。

A.c.1 伴随和其他雅可比 - Adjoint and other trivial Jacobians

根据 $\eqref{1.27.a}$ 、第 2.2 节和上述性质，下列标量导数块变得微不足道

$$ \begin{align*} \mathbf{Ad} _{\sf R} &= 1 & \in \mathbb R \tag{A.7.a}\label{A.7.a} \newline \mathbf J^{\mathsf R^{-1}} _{\sf R} &= -1 & \in \mathbb R \tag{A.7.b}\label{A.7.b} \newline \mathbf J^{\mathsf Q \circ \mathsf R} _{\sf Q} = \mathbf J^{\mathsf Q \circ \mathsf R} _{\sf R} &= 1 & \in \mathbb R \tag{A.7.c}\label{A.7.c} \newline \mathbf J_r(\theta) = \mathbf J_l(\theta) &= 1 & \in \mathbb R \tag{A.7.d} \label{A.7.d} \newline \mathbf J^{\mathsf R \oplus \theta} _{\sf R} = \ \ \mathbf J^{\mathsf R \oplus \theta} _\theta &= 1 & \in \mathbb R \tag{A.7.e}\label{A.7.e} \newline \mathbf J^{\mathsf Q \ominus \mathsf R} _{\sf Q} = -\mathbf J^{\mathsf Q \ominus \mathsf R} _{\sf R} &= 1 & \in \mathbb R \tag{A.7.f}\label{A.7.f} \end{align*} $$

A.c.2 旋转操作 - Rotation action

对于 $\mathsf R \cdot \mathbf v$ 的操作，有

$$ \begin{align*} \mathbf J^{\mathsf R \cdot \mathbf v} _{\sf R} &= \lim _{\theta \to 0} \cfrac{\mathbf R \ \rm{Exp}(\theta) \mathbf v - \mathbf R\mathbf v}{\theta} \newline &= \lim _{\theta \to 0} \cfrac{\mathbf R (\mathbf I + [\theta] _\times) \mathbf v - \mathbf R\mathbf v}{\theta} \newline &= \lim _{\theta \to 0} \cfrac{\mathbf R [\theta] _\times \mathbf v}{\theta} = \mathbf R [1] _\times \mathbf v & \in \mathbb R^{2\times1} \tag{A.8.a} \label{A.8.a} \newline \mathbf J^{\mathsf R \cdot \mathbf v} _{\bf v} &= \cfrac{D\bf Rv}{D\bf v} = \mathbf R & \in \mathbb R^{2\times2} \tag{A.8.b} \label{A.8.b} \end{align*} $$

附录 B: 3D 旋转群 $S^3$ 和 $SO(3)$ - APPENDIX B: THE 3D ROTATION GROUPS $S^3$ AND $SO(3)$

$S^3$ 李群是四元数乘法下的单位四元数群。它的拓扑结构是 $\mathbb R^4$ 中的单位球 (3-sphere) ，因此得名 $S^3$。四元数（深入参考资料请查阅 ⁹）可以用以下两种等价形式表示， $$ \begin{align*} \mathbf q &= w + ix + jy + kz = w + \mathbf v & \in \mathbb H \newline &= \begin{bmatrix} w & x & y & z \end{bmatrix}^\top = \begin{bmatrix} w \newline \bf v \end{bmatrix} & \in \mathbb H \end{align*} \tag{B.1} \label{B.1} $$ 其中，$w、x、y、z \in \mathbb R$ ，$i,j,k$ 是三个单位虚数，使得 $i^2 = j^2 = k^2 = ijk = -1$ 。标量 $w$ 称为标量或实部，$\mathbf v \in \mathbb H_p$ 称为矢量或虚部。我们注意到 $\mathbb H_p$ 是纯四元数的集合，即标量部分为空，维数为 $3$ 。通过共轭 $\mathbf q^{-1} = \mathbf q^∗$ （其中 $\mathbf q^∗ \triangleq w - \mathbf v$ 为共轭）和乘积 $\mathbf q_a \circ \mathbf q_b = \mathbf q_a \mathbf q_b$ 来实现求逆和乘法。

$SO(3)$ 群是三维空间中矩阵乘法下的特殊正交矩阵群，或称旋转矩阵群。与所有 $SO(n)$ 群一样，通过转置和乘积可以实现求逆和复合。

这两个群都可以旋转 3 维向量。它们有同构的切空间，其元素可与 $\mathbb R^3$ 中的旋转向量相识别，因此我们将它们放在一起研究。在这个空间 $\mathbb R^3$ 中，我们定义了旋转率 $\boldsymbol\omega \triangleq \mathbf u \theta$ 角度轴 $\boldsymbol\theta \triangleq \mathbf u \theta$ 以及所有扰动和不确定性的向量。四元流形 $S^3$ 是 $SO(3)$ 的双覆盖，即 $\bf q$ 和 $-\bf q$ 代表相同的旋转 $\bf R$。第一个覆盖对应于实部为正 $w > 0$ 的四元数，这时候这两个群可以被视为同构。

B.a 指数和对数映射 - Exp and Log maps

对于 $S^3$ 的四元数和 $SO(3)$ 的旋转矩阵，可以定义 $\rm Exp$ 映射和 $\rm Log$ 映射。对于四元数 $\mathbf q = (w, \mathbf v) \in \mathbb H$，有（见 Ex. 5 ）

$$ \begin{align*} \mathbf q = {\rm Exp}(\theta \mathbf u) &\triangleq \cos(\theta/2) + \mathbf u \sin(\theta/2) && \in \mathbb H \tag{B.2.a} \label{B.2.a} \newline \theta \mathbf u = {\rm Log}(\mathbf q) &\triangleq 2\mathbf v \cfrac{\arctan(\lVert \mathbf v \rVert, w)}{\lVert \mathbf v \rVert} && \in \mathbb R^3 \tag{B.2.b} \label{B.2.b} \end{align*} $$

在求对数之前，我们可以确保 $\bf q$ 的标量部分 $w$ 为正值，从而避免因 $\bf q$ 的双重覆盖而产生的问题。如果不是，我们可以在对数之前用 $-\bf q$ 代替 $\bf q$ 。对于旋转矩阵，有（见 Ex. 4 ）

$$ \begin{align*} \mathbf R = {\rm Exp}(\theta \mathbf u) &\triangleq \mathbf I + \sin\theta[\mathbf u] _\times + (1-\cos\theta)[\mathbf u] _\times^2 && \in \mathbb R^{3\times3} \tag{B.3.a} \label{B.3.a} \newline \theta \mathbf u = {\rm Log} (\mathbf R) &\triangleq \cfrac{\theta(\mathbf R - \mathbf R^\top)^\vee}{2\sin\theta},\quad \theta = \cos^{-1} \Big(\cfrac{\mathrm{trace}(\mathbf R) - 1}{2}\Big) && \in \mathbb R^3 \tag{B.3.b} \label{B.3.b} \end{align*} $$

B.b 旋转操作 - Rotation action

根据上述四元数和旋转矩阵的表达式，四元数对 3 维向量的旋转作用是通过双四元数乘积来实现的， $$ \mathbf x’ = \mathbf{q \ x \ q}^* \tag{B.4} \label{B.4} $$ 而旋转矩阵使用单一矩阵乘积 $$ \mathbf x’ = \bf Rx \tag{B.5}\label{B.5} $$ 两者都对应于绕轴 $\bf u$ 右手旋转 $\theta \ \rm rad$ 角度。将 $\bf x$ 与 $\mathbf x^′$ 对等识别，可得到同一性

$$ \mathbf R(\mathbf q) = \begin{bmatrix} w^2 + x^2 - y^2 - z^2 & 2(xy-wz) & 2(xz+wy) \newline 2(xy+wz) & w^2 -x^2 + y^2 - z^2 & 2(yz-wx) \newline 2(xz-wy) & 2(yz+wx) & w^2 - x^2 -y^2 + z^2 \end{bmatrix} \tag{B.6} \label{B.6} $$

B.c 基本雅可比块 - Elementary Jacobian blocks

由于我们定义的导数映射切向量空间，而这些空间对于 $S^3$ 和 $SO(3)$ 的三维旋转流形是重合的，即 $\boldsymbol\theta = {\rm Log}(\mathbf q) = {\rm Log}(\mathbf R)$，因此雅各比值与所使用的表示（$\bf q$ 或 $\bf R$）无关。因此，我们考虑一般的三维旋转元素，并用无衬线字体 $\sf R$ 表示

B.c.1 伴随 - Adjoint

根据 $\eqref{1.19}$ 可以得出

$$ {\bf Ad} _{\sf R} \boldsymbol\theta = (\mathbf R[\boldsymbol\theta] _\times \mathbf R^\top)^\vee = ([(\mathbf R \boldsymbol\theta)] _\times)^\vee = \mathbf R \boldsymbol\theta $$

因此有，

$$ {\bf Ad}_{\sf R} = \bf R \tag{B.7} \label{B.7} $$

这意味着 ${\bf Ad_q} = \mathbf R(\mathbf q)$，见 $\eqref{B.6}$ ，以及 ${\bf Ad_R} = \bf R$

B.c.2 逆、复合 - Inversion, composition

从第 2 节中我们可以看出，

$$ \begin{align*} \mathbf J _{\sf R}^{\mathsf R^{-1}} &= - {\bf Ad} _{\sf R} = - \mathbf R \tag{B.8.a} \label{B.8.a} \newline \mathbf J _{\sf Q}^{\sf QR} &= {\bf Ad} _{\sf R} {}^{-1} = \mathbf R^\top \tag{B.8.b} \label{B.8.b} \newline \mathbf J _{\sf R}^{\sf QR} &= \mathbf I \tag{B.8.c} \label{B.8.c} \end{align*} $$

B.c.3 右和左雅可比 - Right and left Jacobians

它们采用封闭形式 [¹⁰, 第 40 页］，

$$ \begin{align*} \mathbf J_r(\boldsymbol\theta) &= \mathbf I - \frac{1 - \cos\theta}{\theta^2}[\boldsymbol\theta] _\times + \frac{\theta - \sin\theta}{\theta^3}[\boldsymbol\theta] _\times^2 \tag{B.9.a} \label{B.9.a} \newline \mathbf J_r^{-1}(\boldsymbol\theta) &= \mathbf I + \frac12[\boldsymbol\theta] _\times + \Big( \frac1{\theta^2} - \frac{1+\cos\theta}{2\theta\sin\theta} \Big) [\boldsymbol\theta] _\times^2 \tag{B.9.b} \label{B.9.b} \newline \mathbf J_l(\boldsymbol\theta) &= \mathbf I + \frac{1-\cos\theta}{\theta^2} [\boldsymbol\theta] _\times + \frac{\theta - \sin\theta}{\theta^3}[\boldsymbol\theta] _\times^2 \tag{B.9.c} \label{B.9.c} \newline \mathbf J_l^{-1}(\boldsymbol\theta) &= \mathbf I - \frac12[\boldsymbol\theta] _\times + \Big( \frac1{\theta^2} - \frac{1+\cos\theta}{2\theta\sin\theta} \Big) [\boldsymbol\theta] _\times^2 \tag{B.9.d} \label{B.9.d} \newline \end{align*} $$

可以观察到

$$ \mathbf J_l = \mathbf J_r^\top \qquad \mathbf J_l^{-1} = \mathbf J_r^{-\top} \tag{B.10} \label{B.10} $$

B.c.4 右加和减 - Right- plus and minus

对于 $\boldsymbol\theta = \sf Q \ominus R$，有

$$ \begin{align*} \mathbf J_{\sf R}^{\mathsf R \oplus \boldsymbol\theta} &= \mathbf R(\boldsymbol\theta)^\top & \mathbf J_{\boldsymbol\theta}^{\mathsf R \oplus \boldsymbol\theta} &= \mathbf J_r(\boldsymbol\theta) \tag{B.11.a} \label{B.11.a} \newline \mathbf J_{\sf Q}^{\sf Q \ominus R} &= \mathbf J_r^{-1}(\boldsymbol\theta) & \mathbf J_{\sf R}^{\sf Q \ominus R} &= -\mathbf J_l^{-1}(\boldsymbol\theta) \tag{B.11.b} \label{B.11.b} \end{align*} $$

B.c.5 旋转操作 - Rotation action

有

$$ \begin{align*} \mathbf J _{\sf R}^{\mathsf R\cdot\mathbf v} &\triangleq \lim _{\boldsymbol\theta \to 0} \frac{(\mathbf R \oplus \boldsymbol\theta) \mathbf v - \mathbf{Rv}}{\boldsymbol\theta} = \newline \lim _{\boldsymbol\theta \to 0} \frac{\mathbf R \rm{Exp}(\boldsymbol\theta) \mathbf v - \mathbf{Rv}}{\boldsymbol\theta} &= \lim _{\boldsymbol\theta \to 0} \frac{\mathbf R (\mathbf I + [\boldsymbol\theta] _\times) \mathbf v - \mathbf{Rv}}{\boldsymbol\theta} \newline = \lim _{\boldsymbol\theta \to 0} \frac{\mathbf R [\boldsymbol\theta] _\times \mathbf v }{\boldsymbol\theta} &= \lim _{\boldsymbol\theta \to 0} \frac{-\mathbf R [\mathbf v] _\times \boldsymbol\theta }{\boldsymbol\theta} = -\mathbf R [\mathbf v] _\times \end{align*} \tag{B.12} \label{B.12} $$

其中我们使用了 ${\rm Exp}(\boldsymbol\theta) \approx \mathbf I + [\boldsymbol\theta] _\times$ 和 $[\mathbf a] _\times \mathbf b = -[\mathbf b] _\times \mathbf a$ 的性质，

$$ \mathbf J_{\bf v}^{\mathsf R \cdot \mathbf v} \triangleq \lim_{\partial \mathbf v \to 0} \frac{\mathbf R (\mathbf v + \partial \mathbf v) - \bf Rv}{\partial\bf v} = \mathbf R \tag{B.13} \label{B.13} $$

附录 C: 二维刚性运动群 $SE(2)$ - THE 2D RIGID MOTION GROUP $SE(2)$

我们把刚体运动群 $SE(2)$ 的元素写成

$$ \mathbf M = \begin{bmatrix} \bf R & \bf t \newline \bf 0 & 1 \end{bmatrix} \in SE(2) \subset \mathbb R^{3\times3} \tag{C.1}\label{C.1} $$

其中 $\mathbf R \in SO(2)$ 表示旋转，$\mathbf t \in \mathbb R^2$ 表示平移。李代数和向量切线由以下类型的元素构成

$$ \boldsymbol\tau^\wedge = \begin{bmatrix} [\theta]_\times & \boldsymbol\rho \newline \bf 0 & 0 \end{bmatrix} \in \mathfrak{se}(2), \quad \boldsymbol\tau = \begin{bmatrix} \boldsymbol\rho \newline \theta \end{bmatrix} \tag{C.2} \label{C.2} $$

C.a 逆、复合 - Inverse, composition

逆和复合分别通过矩阵逆和乘积进行

$$ \begin{align*} \mathbf M^{-1} &= \begin{bmatrix} \bf R^\top & -\bf R^\top t \newline \bf 0 & 1 \end{bmatrix} \tag{C.3.a} \label{C.3.a} \newline \mathbf M_a \mathbf M_b &= \begin{bmatrix} \mathbf R_a \mathbf R_b & \mathbf t_a + \mathbf R_a \mathbf t_b \newline \bf 0 & 1 \end{bmatrix} \tag{C.3.b} \label{C.3.b} \end{align*} $$

C.b 指数和对数映射 - Exp and Log maps

$\rm Exp$ 和 $\rm Log$ 是通过指数映射直接从标量切空间 $\mathbb R^3 \cong {\mathfrak se}(2) = TSE(2)$ 实现的，推导过程见 ⁶

$$ \begin{align*} \mathbf M = {\rm Exp}(\boldsymbol\tau) &\triangleq \begin{bmatrix} {\rm Exp}(\theta) & \mathbf V(\theta)\boldsymbol\rho \newline \bf 0 & 1 \end{bmatrix} \tag{C.4.a} \label{C.4.a} \newline \boldsymbol\tau = {\rm Log}(\mathbf M) &\triangleq \begin{bmatrix} \mathbf V^{-1}(\theta) \ \bf t \newline {\rm Log}(\mathbf R) \end{bmatrix} \tag{C.4.b} \label{C.4.b} \newline {\text 其中，} \quad \mathbf V(\theta) &= \frac{\sin\theta}\theta \mathbf I + \frac{1 - \cos\theta}\theta [1]_\times \end{align*} $$

C.c 雅可比块 - Jacobian blocks

C.c.1 伴随 - Adjoint

利用平面旋转相通的事实，可以很容易地从 $\eqref{1.19}$ 求出邻接点

$$ {\bf Ad_M \boldsymbol\tau} = (\mathbf M \boldsymbol\tau^\wedge \mathbf M^{-1})^\vee = \begin{bmatrix} \mathbf R \boldsymbol\rho - [\theta]_\times \ \bf t \newline \theta \end{bmatrix} = {\bf Ad_M} \begin{bmatrix} \boldsymbol\rho \newline \theta \end{bmatrix} $$

得到

$$ {\rm Ad_M} = \begin{bmatrix} \bf R & -[1]_\times \bf t \newline \bf 0 & 1 \end{bmatrix} \tag{C.5} \label{C.5} $$

C.c.2 逆、复合 - Inversion, composition

从第 2.2 节我们可以得出

$$ \begin{align*} {\bf J_M^{M^{-1}}} &= -{\bf Ad_M} = \begin{bmatrix} -\bf R & [1] _\times \bf t \newline \bf 0 & -1 \end{bmatrix} \tag{C.6.a} \label{C.6.a} \newline \mathbf J _{\mathbf M_a}^{\mathbf M_a \mathbf M_b} &= \mathbf{Ad} _{\mathbf M_b}{}^{-1} = \begin{bmatrix} \mathbf R_b^\top & \mathbf R_b^\top [1] _\times \mathbf t_b \newline \bf 0 & 1 \end{bmatrix} \tag{C.6.b} \label{C.6.b} \newline \mathbf J _{\mathbf M_b}^{\mathbf M_a \mathbf M_b} &= \mathbf I \tag{C.6.c} \label{C.6.c} \end{align*} $$

C.c.3 右和左雅可比 - Right and left Jacobians

我们从[¹⁰，第 36 页]中得出结论

$$ \begin{align*} \mathbf J_r &= \begin{bmatrix} \sin\theta / \theta & (1-\cos\theta) / \theta & (\theta\rho_1 - \rho_2 + \rho_2\cos\theta - \rho_1 \sin\theta) / \theta^2 \newline (\cos\theta -1) / \theta & \sin\theta / \theta & (\rho_1 + \theta\rho_2 - \rho_1 \cos\theta - \rho_2\sin\theta) / \theta^2 \newline 0 & 0 & 1 \end{bmatrix} \tag{C.7.a} \label{C.7.a} \newline \mathbf J_l &= \begin{bmatrix} \sin\theta / \theta & (\cos\theta-1) / \theta & (\theta\rho_1 + \rho_2 - \rho_2\cos\theta - \rho_1 \sin\theta) / \theta^2 \newline (1-\cos\theta) / \theta & \sin\theta / \theta & (-\rho_1 + \theta\rho_2 + \rho_1 \cos\theta - \rho_2\sin\theta) / \theta^2 \newline 0 & 0 & 1 \end{bmatrix} \tag{C.7.b} \label{C.7.b} \end{align*} $$

C.c.4 刚性运动运算 - Rigid motion action

在点 $\bf p$ 上采取行动

$$ \mathbf M \cdot \mathbf p \triangleq \mathbf t + \bf Rp \tag{C.8} \label{C.8} $$

因此，对于 $\boldsymbol\tau \to 0$，我们有 ${\rm Exp}(\boldsymbol\tau) \to \mathbf I + \boldsymbol\tau^\wedge$ ，

$$ \begin{align*} {\bf J_M^{M\cdot p}} &= \lim_{\boldsymbol\tau \to 0} \frac{\mathbf M \ {\rm Exp}(\boldsymbol\tau) \cdot \mathbf p - \mathbf M \cdot \mathbf p}{\boldsymbol\tau} = \begin{bmatrix} \bf R & \mathbf R [1]_\times \bf p \end{bmatrix} \tag{C.9.a} \label{C.9.a} \newline {\bf J_p^{M\cdot p}} &= \mathbf R \tag{C.9.b} \label{C.9.b} \end{align*} $$

附录 D: 三维刚性运动群 $SE(3)$ - THE 3D RIGID MOTION GROUP $SE(3)$

我们将三维刚性运动群 $SE(3)$ 的元素写成

$$ \mathbf M = \begin{bmatrix} \bf R & \bf t \newline \bf 0 & 1 \end{bmatrix} \in SE(3) \subset \mathbb R^{4\times4} \tag{D.1} \label{D.1} $$

其中 $\mathbf R \in SO(3)$ 为旋转矩阵，$\mathbf t \in \mathbb R^3$ 为平移向量。李代数和向量切线由以下类型的元素构成

$$ \boldsymbol\tau^\wedge = \begin{bmatrix} [\boldsymbol\theta]_\times & \boldsymbol\rho \newline \mathbf 0 & 0 \end{bmatrix} \in {\frak se}(3) \quad , \qquad \boldsymbol\tau = \begin{bmatrix} \boldsymbol\rho \newline \boldsymbol\theta \end{bmatrix} \in \mathbb R^6 \tag{D.2} \label{D.2} $$

D.a 逆、复合 - Inverse, composition

逆和合成分别通过矩阵逆和乘积进行

$$ \begin{align*} \mathbf M^{-1} &= \begin{bmatrix} \mathbf R^\top & -\bf R^\top t \newline \bf 0 & 1 \end{bmatrix} \tag{D.3.a} \label{D.3.a} \newline \mathbf M^{-1} &= \begin{bmatrix} \mathbf R_a \mathbf R_b & \mathbf t_a + \mathbf R_a \mathbf t_b \newline \bf 0 & 1 \end{bmatrix} \tag{D.3.b} \label{D.3.b} \end{align*} $$

D.b 指数和对数映射 - Exp and Log maps

$\rm Exp$ 和 $\rm Log$ 是通过直接从向量切空间 $\mathbb R^6 \cong {\frak se}(3) = TSE(3)$ 的指数映射实现的，推导过程见 ⁶

$$ \begin{align*} \mathbf M = {\rm Exp}(\boldsymbol\tau) &\triangleq \begin{bmatrix} {\rm Exp}(\boldsymbol\theta) & \mathbf V(\boldsymbol\theta) \boldsymbol\rho \newline \mathbf 0 & 1 \end{bmatrix} \tag{D.4.a} \label{D.4.a} \newline \boldsymbol\tau = {\rm Log}(\mathbf M) &\triangleq \begin{bmatrix} \mathbf V^{-1}(\boldsymbol\theta) \ \mathbf t \newline {\rm Log}(\mathbf R) \end{bmatrix} \tag{D.4.b} \label{D.4.b} \end{align*} $$

与（回顾 ${\rm Log}(\mathbf M)$，$\boldsymbol\theta = \theta \mathbf u = {\rm Log}(\mathbf R)$ )，

$$ \mathbf V(\boldsymbol\theta) = \mathbf I + \frac{1-\cos\theta}{\theta^2} [\boldsymbol\theta] _\times + \frac{\theta - \sin\theta}{\theta^3} [\boldsymbol\theta]^2 _\times \tag{D.5} \label{D.5} $$

注意，这与 $\eqref{B.9.c}$ 完全吻合。

D.c 雅可比块 - Jacobian blocks

D.c.1 伴随 - Adjoint

有（看 Ex. 6））

$$ {\bf Ad_M} \boldsymbol\tau = (\mathbf M \boldsymbol\tau^\wedge \mathbf M^{-1})^\vee = \begin{bmatrix} \mathbf R \boldsymbol\rho + [\mathbf t]_\times \mathbf R \boldsymbol\theta \newline \mathbf R \boldsymbol\theta \end{bmatrix} = {\bf Ad_M} \begin{bmatrix} \boldsymbol\rho \newline \boldsymbol\theta \end{bmatrix} $$

因此，

$$ {\bf Ad_M} = \begin{bmatrix} \mathbf R & [\mathbf t]_\times \mathbf R \newline \mathbf 0 & \mathbf R \end{bmatrix} \in \mathbb R^{6\times6} \tag{D.6} \label{D.6} $$

D.c.2 逆、复合 - Inversion, composition

从第 2.2 节我们可以得出

$$ \begin{align*} {\bf J_M^{M^{-1}}} &= -{\bf Ad_M} = -\begin{bmatrix} \bf R & [\mathbf t] _\times \bf R \newline \bf 0 & \bf R \end{bmatrix} \tag{D.7.a} \label{D.7.a} \newline \mathbf J _{\mathbf M_a}^{\mathbf M_a \mathbf M_b} &= \mathbf{Ad} _{\mathbf M_b}{}^{-1} = \begin{bmatrix} \mathbf R_b^\top & - \mathbf R_b^\top [\mathbf t_b] _\times \newline \bf 0 & \mathbf R_b^\top \end{bmatrix} \tag{D.7.b} \label{D.7.b} \newline \mathbf J _{\mathbf M_b}^{\mathbf M_a \mathbf M_b} &= \mathbf I_6 \tag{D.7.c} \label{D.7.c} \end{align*} $$

D.c.3 右和左雅可比 - Right and left Jacobians

Barfoot 在 ⁵ 中给出了左雅各布及其逆的封闭形式，

$$ \begin{align*} \mathbf J_l(\boldsymbol\rho, \boldsymbol\theta) &= \begin{bmatrix} \mathbf J_l(\boldsymbol\theta) & \mathbf Q(\boldsymbol\rho, \boldsymbol\theta) \newline \mathbf 0 & \mathbf J_l(\boldsymbol\theta) \end{bmatrix} \tag{D.8.a} \label{D.8.a} \newline \mathbf J_l^{-1}(\boldsymbol\rho, \boldsymbol\theta) &= \begin{bmatrix} \mathbf J_l^{-1}(\boldsymbol\theta) & -\mathbf J_l^{-1}(\boldsymbol\theta) \mathbf Q(\boldsymbol\rho, \boldsymbol\theta) \mathbf J_l^{-1}(\boldsymbol\theta) \newline \mathbf 0 & \mathbf J_l^{-1}(\boldsymbol\theta) \end{bmatrix} \tag{D.8.b} \label{D.8.b} \end{align*} $$

其中，$\mathbf J_l(\boldsymbol\theta)$ 是 $SO(3)$ 的左雅各布，见 $\eqref{B.9.c}$ ，以及

$$ \begin{align*} \mathbf Q(\boldsymbol\rho, \boldsymbol\theta) =& \frac12 \boldsymbol\rho_\times + \frac{\theta - \sin\theta}{\theta^3}(\boldsymbol\theta_\times \boldsymbol\rho_\times + \boldsymbol\rho_\times \boldsymbol\theta_\times + \boldsymbol\theta_\times \boldsymbol\rho_\times \boldsymbol\theta_\times) \newline &-\frac{1-\frac{\theta^2}{2} - \cos\theta}{\theta^4}(\boldsymbol\theta_\times^2 \boldsymbol\rho_\times + \boldsymbol\rho_\times \boldsymbol\theta_\times^2 + 3 \boldsymbol\theta_\times \boldsymbol\rho_\times \boldsymbol\theta_\times) \newline &-\frac12 \Big( \frac{1-\frac{\theta^2}{2} - \cos\theta}{\theta^4} - 3 \frac{\theta - \sin\theta - \frac{\theta^3}{6}}{\theta^5} \Big) (\boldsymbol\theta_\times \boldsymbol\rho_\times \boldsymbol\theta_\times^2 + \boldsymbol\theta_\times^2 \boldsymbol\rho_\times \boldsymbol\theta_\times) \end{align*} \tag{D.9} \label{D.9} $$

利用 $\eqref{2.13}$ 可以得到右雅各布及其逆，即 $\mathbf J_r(\boldsymbol\rho, \boldsymbol\theta) = \mathbf J_l(-\boldsymbol\rho, -\boldsymbol\theta)$ 和 $\mathbf J_r^{-1}(\boldsymbol\rho, \boldsymbol\theta) = \mathbf J_l^{-1}(-\boldsymbol\rho, -\boldsymbol\theta)$ 。

D.c.4 刚性运动运算 - Rigid motion action

在点 $\bf p$ 上采取行动

$$ \mathbf M \cdot \mathbf p \triangleq \mathbf t + \bf Rp \tag{D.10} \label{D.10} $$

因此，对于 $\boldsymbol\tau \to 0$，我们有 ${\rm Exp}(\boldsymbol\tau) \to \mathbf I + \boldsymbol\tau^\wedge$ ，

$$ \begin{align*} {\bf J_M^{M\cdot p}} &= \lim_{\boldsymbol\tau \to 0} \frac{\mathbf M \ {\rm Exp}(\boldsymbol\tau) \cdot \mathbf p - \mathbf M \cdot \mathbf p}{\boldsymbol\tau} = \begin{bmatrix} \bf R & -\mathbf R [\mathbf p]_\times \end{bmatrix} \tag{D.10.a} \label{D.10.a} \newline {\bf J_p^{M\cdot p}} &= \mathbf R \tag{D.10.b} \label{D.10.b} \end{align*} $$

附录 E: 变换群 $(\mathbb R^n, +)$ 和 $T(n)$ - THE TRANSLATION GROUPS $(\mathbb R^n, +)$ AND $T(n)$

群 $(\mathbb R^n, +)$ 是加法下的向量群，可视为平移群。我们认为它是微不足道的，因为它的群元、李代数和切空间都是相同的，所以 $\mathbf t = \mathbf t^\wedge = {\rm Exp}(\mathbf t)$。它的等价矩阵群（乘法下）是平移群 $T(n)$，其群元、李代数和切向量元分别为

$$ \mathbf T \triangleq \begin{bmatrix} \mathbf I & \mathbf t \newline \mathbf 0 & 1 \end{bmatrix} \in T(n) \ , \quad \mathbf t^\wedge \triangleq \begin{bmatrix} \bf 0 & \bf t \newline \bf 0 & 0 \end{bmatrix} \in \mathbf t(n) \ , \quad \mathbf t \in \mathbb R^n $$

通过观察 ${\bf T(0)} = \bf I$，$\mathbf T(-\mathbf t) = \mathbf T(\mathbf t)^{-1}$，以及换元组合很容易验证等价性

$$ \mathbf T_1 \mathbf T_2 = \begin{bmatrix} \bf I & \mathbf t_1 + \mathbf t_2 \newline \bf 0 & 1 \end{bmatrix} $$

实际上是将向量 $\mathbf t_1$ 和 $\mathbf t_2$ 相加。由于 $\mathbb R^n$ 中的和是交换式的，因此 $T(n)$ 中的构成积也是交换式的。由于 $T(n)$ 是 $\mathbf R = \mathbf I$ 的 $SE(n)$ 子群，我们可以通过取 $\mathbf R = \bf I$ 的 $\eqref{C.4.a}\eqref{D.4.a}$ 并推广到任意 $n$ 来轻松确定其指数映射

$$ {\rm Exp}: \quad \mathbb R^n \to T(n) \ ; \quad \mathbf T = {\rm Exp}(\mathbf t) = \begin{bmatrix} \mathbf I & \mathbf t \newline \mathbf 0 & 1 \end{bmatrix} \tag{E.1} \label{E.1} $$

$T(n)$ 指数也可以从 $\exp(\mathbf t^\wedge)$ 的泰勒展开得到，注意 $(\mathbf t^\wedge)^2 = 0$ 。这就直接证明了 $(\mathbb R^n, +)$ 群的等效指数，即同一性

$$ {\rm Exp}: \quad \mathbb R^n \to \mathbb R^n \quad \mathbf t = {\rm Exp}(\mathbf t) \tag{E.2} \label{E.2} $$

这就派生出 $\mathbb R^n$ 中的三元、交换、左右同向、加减算子

$$ \begin{align*} \mathbf t_1 \oplus \mathbf t_2 &= \mathbf t_1 + \mathbf t_2 \tag{E.3.a} \label{E.3.a} \newline \mathbf t_2 \ominus \mathbf t_2 &= \mathbf t_2 - \mathbf t_1 \tag{E.3.b} \label{E.3.b} \end{align*} $$

E.a 雅可比块 - Jacobian blocks

我们将 $T(n)$ 和 $\mathbb R^n$ 的平移模糊地表示出来，并将它们记为 $\sf S$ 和 $\sf T$ 。它们的雅各布简是微不足道的（A.c.1 节中 $S^1$ 和 $SO(2)$ 的雅各布简相比较）

$$ \begin{align*} {\bf AD} _{\sf T} &= \mathbf I & \in \mathbb R^{n\times n} \tag{E.4.a} \label{E.4.a} \newline \mathbf J _{\sf T}^{\mathsf T^{-1}} &= -\mathbf I & \in \mathbb R^{n\times n} \tag{E.4.b} \label{E.4.b} \newline \mathbf J _{\sf T}^{\sf T \circ S} = \mathbf J _{\sf S}^{\sf T \circ S} &= \mathbf I & \in \mathbb R^{n\times n} \tag{E.4.c} \label{E.4.c} \newline \mathbf J_r = \mathbf J_l &= \mathbf I & \in \mathbb R^{n\times n} \tag{E.4.d} \label{E.4.d} \newline \mathbf J _{\sf T}^{\mathsf T \oplus \mathbf v} = \mathbf J _{\bf v}^{\mathsf T \oplus \mathbf v} &= \mathbf I & \in \mathbb R^{n\times n} \tag{E.4.e} \label{E.4.e} \newline \mathbf J _{\sf S}^{\sf S \ominus T} = -\mathbf J _{\sf T}^{\sf S \ominus T} &= \mathbf I & \in \mathbb R^{n\times n} \tag{E.4.f} \label{E.4.f} \end{align*} $$

Reference

Joan Sola, Jeremie Deray, Dinesh Atchuthan, A micro Lie theory for state estimation in robotics, Lie theory cheat sheet, arXiv:1812.01537v9 [cs.RO] 8 Dec 2021. ↩︎ ↩︎
H. Abbaspour and M. Moskowitz, Basic Lie Theory. WORLD SCIENTIFIC, 2007. [Online]. Available: https://worldscientific.com/ doi/abs/10.1142/6462 ↩︎
R. Howe, “Very basic Lie theory,” The American Mathematical Monthly, vol. 90, pp. 600–623, 1983. ↩︎ ↩︎
J. Stillwell, Naive Lie Theory. Springer-Verlag New York, 2008. ↩︎ ↩︎ ↩︎
T. D. Barfoot, State Estimation for Robotics. Cambridge University Press, 2017. ↩︎ ↩︎
E. Eade, “Lie groups for 2D and 3D transformations,” Tech. Rep. ↩︎ ↩︎ ↩︎ ↩︎
C. Forster, L. Carlone, F. Dellaert, and D. Scaramuzza, “On-manifold preintegration for real-time visual–inertial odometry,” IEEE Transactions on Robotics, vol. 33, no. 1, pp. 1–21, 2017. ↩︎
J. Deray and J. Sola, “Manif: A micro lie theory library for state estimation in robotics applications,” Journal of Open Source Software, vol. 5, no. 46, p. 1371, 2020. [Online]. Available: https://doi.org/10.21105/joss.01371 ↩︎
J. Sola, “Quaternion kinematics for the error-state Kalman filter,” CoRR, vol. abs/1711.02508, 2017. [Online]. Available: http://arxiv.org/abs/1711.02508 ↩︎ ↩︎
G. Chirikjian, Stochastic Models, Information Theory, and Lie Groups, Volume 2: Analytic Methods and Modern Applications, ser. Applied and Numerical Harmonic Analysis. Birkh¨auser Boston, 2011. [Online]. Available: https://books.google.ch/books?id=hZ1CAAAAQBAJ ↩︎ ↩︎ ↩︎
M. Kaess, H. Johannsson, R. Roberts, V. Ila, J. Leonard, and F. Dellaert, “iSAM2: Incremental smoothing and mapping with fluid relineariza- tion and incremental variable reordering,” in Robotics and Automation (ICRA), 2011 IEEE International Conference on, May 2011, pp. 3281– 3288. ↩︎ ↩︎
F. Dellaert and M. Kaess, “Square Root SAM: Simultaneous Localiza- tion and Mapping via Square Root Information Smoothing,” vol. 25, no. 12, pp. 1181–1203, 2006. ↩︎ ↩︎
R. Kummerle, G. Grisetti, H. Strasdat, K. Konolige, and W. Burgard, “G2o: A general framework for graph optimization,” in Robotics and Automation (ICRA), 2011 IEEE International Conference on, May 2011, pp. 3607–3613. ↩︎
V. Ila, L. Polok, M. Solony, and P. Svoboda, “SLAM++ - a highly efficient and temporally scalable incremental SLAM framework,” The International Journal of Robotics Research, vol. 36, no. 2, pp. 210–230, 2017. [Online]. Available: https://doi.org/10.1177/0278364917691110 ↩︎

A micro Lie theory for state estimation in robotics 1#

1. 微观的李氏理论 - A MICRO LIE THEORY#

1.1 李群 - The Lie group#

1.2 群运算 - The group actions#

1.3 切线空间和李代数 - The tangent spaces and the Lie algebra#

1.3.1 李代数 $\mathfrak m$#

1.3.2 笛卡尔向量空间 $\mathbb R^m$#

1.4 指数映射 - The exponential map#

1.4.1 大写的指数映射 - The capitalized exponential map#

1.5 加减运算 - Plus and minus operators#

1.6 伴随及伴随矩阵 - The adjoint, and the adjoint matrix#

1.6.1 伴随#

1.6.2 伴随矩阵#

1.7 李群的导数 - Derivatives on Lie groups#

1.7.1 向量空间上的雅可比#

1.7.2 李群上的右雅可比#

1.7.3 李群上的左雅可比#

1.7.4 交叉右-左雅可比#

1.8 流形的不确定性与协方差传播 - Uncertainty in manifolds, covariance propagation#

1.9 流形上的离散积分 - Discrete integration on manifolds#

2. 流形上的微分规则 - DIFFERENTIATION RULES ON MANIFOLDS#

2.1 链式法则 - The chain rule#

2.2 基本雅可比块 - Elementary Jacobian blocks#

2.2.1 逆 - Inverse#

2.2.2 复合 - Composition#

2.2.3 $\mathcal M$ 的雅可比 - Jacobians of $\mathcal M$#

2.2.4 群作用 - Group action#

2.3 有用可推导的雅可比块 - Useful, but deduced, Jacobian blocks#

2.3.1 对数映射 - Log map#

2.3.2 加和减 - Plus and minus#

3. 复合流形 - COMPOSITE MANIFOLDS#

4. 基于地标的定位与建图 - LANDMARK-BASED LOCALIZATION AND MAPPING#

4.1 在流形上使用误差状态卡尔曼滤波器进行定位 - Localization with error-state Kalman filter on manifold#

4.2 基于图形优化的平滑与建图 - Smooting and Mapping with graph-based optimization#

4.3 带有自标定的平滑与建图 - Smoothing and mapping with self-calibration#

4.4 3D 实现 - 3D implementations#

5. 总结 - CONCLUSION#

附录 A: 2D 旋转群 $S^1$ 和 $SO(2)$ - APPENDIX A: THE 2D ROTATION GROUPS $S^1$ AND $SO(2)$#

A.a 指数和对数映射 - Exp and Log maps#

A.b 逆、复合、幂映射 - Inverse, composition, exponential map#

A.c 雅可比块 - Jacobian blocks#

A.c.1 伴随和其他雅可比 - Adjoint and other trivial Jacobians#

A.c.2 旋转操作 - Rotation action#

附录 B: 3D 旋转群 $S^3$ 和 $SO(3)$​ - APPENDIX B: THE 3D ROTATION GROUPS $S^3$ AND $SO(3)$#

B.a 指数和对数映射 - Exp and Log maps#

B.b 旋转操作 - Rotation action#

B.c 基本雅可比块 - Elementary Jacobian blocks#

B.c.1 伴随 - Adjoint#

B.c.2 逆、复合 - Inversion, composition#

B.c.3 右和左雅可比 - Right and left Jacobians#

B.c.4 右加和减 - Right- plus and minus#

B.c.5 旋转操作 - Rotation action#

附录 C: 二维刚性运动群 $SE(2)$ - THE 2D RIGID MOTION GROUP $SE(2)$#

C.a 逆、复合 - Inverse, composition#

C.b 指数和对数映射 - Exp and Log maps#

C.c 雅可比块 - Jacobian blocks#

C.c.1 伴随 - Adjoint#

C.c.2 逆、复合 - Inversion, composition#

C.c.3 右和左雅可比 - Right and left Jacobians#

C.c.4 刚性运动运算 - Rigid motion action#

附录 D: 三维刚性运动群 $SE(3)$ - THE 3D RIGID MOTION GROUP $SE(3)$#

D.a 逆、复合 - Inverse, composition#

D.b 指数和对数映射 - Exp and Log maps#

D.c 雅可比块 - Jacobian blocks#

D.c.1 伴随 - Adjoint#

D.c.2 逆、复合 - Inversion, composition#

D.c.3 右和左雅可比 - Right and left Jacobians#

D.c.4 刚性运动运算 - Rigid motion action#

附录 E: 变换群 $(\mathbb R^n, +)$ 和 $T(n)$ - THE TRANSLATION GROUPS $(\mathbb R^n, +)$ AND $T(n)$#

E.a 雅可比块 - Jacobian blocks#

Reference#